1.4.3 boolean algebra

AND

• /\

• 0 0 = 0

• 0 1 = 0

• 1 1 = 1

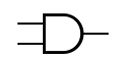
OR

• V

• 0 0 = 0

• 0 1 = 1

• 1 1 = 1

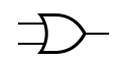
NOT

• 0 = 1

• 1 = 0

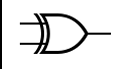
XOR

• V

• 1 0 = 1

• 0 0 = 0

• 1 1 = 0

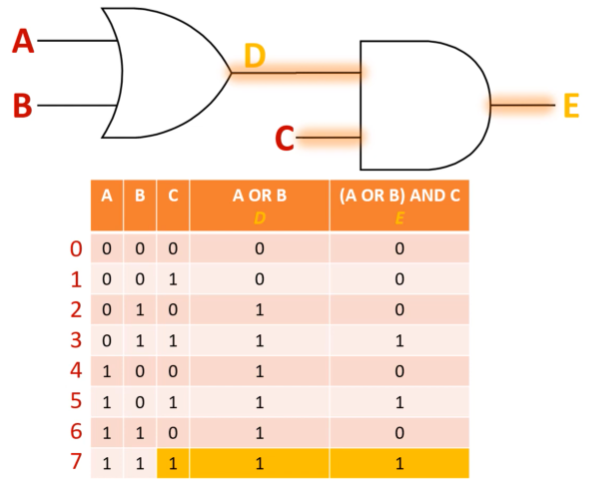
truth table

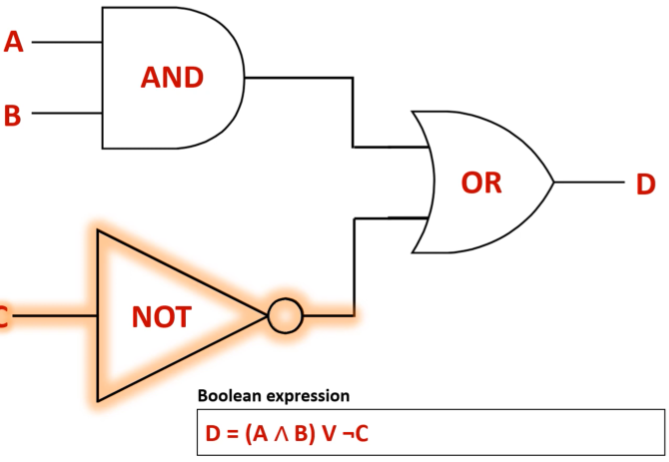
boolean expression

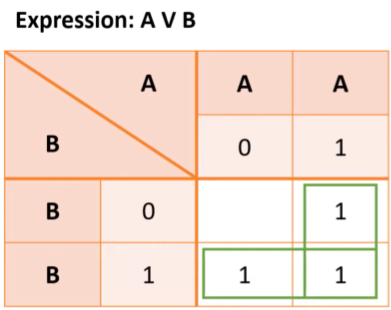
karnaugh maps

• method used to simplify Boolean expressions

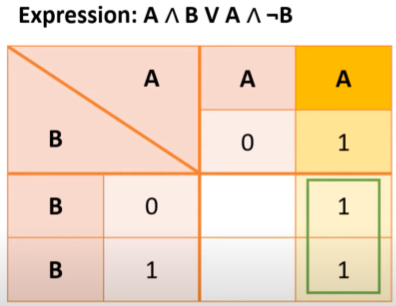
• A OR B shown in image

A /\ N V A /\ NOT B

can be simplified down to just A

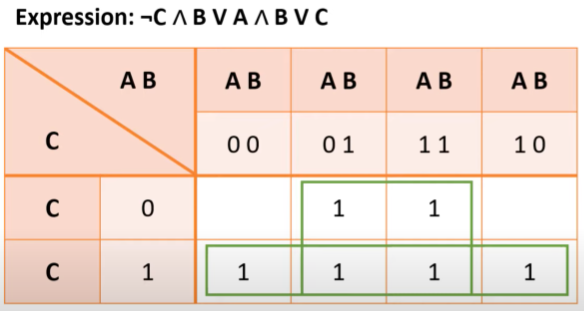
karnaugh map example

• AB - only one digit can be changes at a time so the order is 00, 01, 11, 10

• expression can be simplifies to B V C

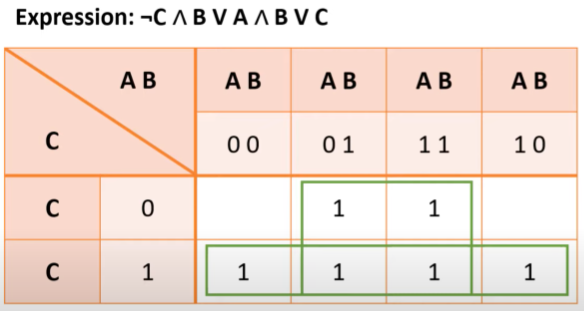
karnaugh map simplification rules

• boxes must be rectangles or squares, no diagonal boxes

• boxes can only contain 1s

• boxes must be as large as possible

• boxes of 2ⁿ 1s: 1, 2 ,4 ,8 ,16

• boxes can overlap

• aim for smallest number of overall boxes

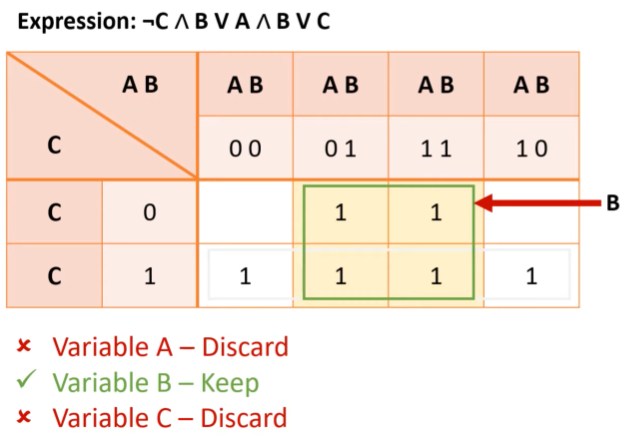
karnaugh map expression simplification

• take each box in any order

• take each variable in any order

• if the digit for the variable in the heading stays the same, keep the variable

• if the digit for the variable in the heading changes, discard the variable

general AND boolean simplification rules

• X AND 0 = 0

• X AND 1 = X

• X AND X = X

• X AND NOT X = 0

general OR boolean simplification rules

• X OR 0 = X

• X OR 1 = 1

• X OR X = X

• X OR NOT X = 1

what does de morgans law do

• a way of simplifying boolean expressions by inverting all the variables

  • changing ANDs to ORs and vice versa

de morgans 1st law

¬(A V B) = ¬A OR ¬B

1. change OR to AND

   1. ¬(A /\ B)

2. NOT the terms on either side of the operator

   1. ¬(¬A /\ ¬B)

3. NOT everything that has changed

   1. ¬¬(¬A /\ ¬B)

   2. get rid of double negation

   3. = ¬A /\ ¬B

de morgans 2nd law

• ¬(A ∨ B) ≡ ¬A ∧ ¬B

• NOT (A OR B) is the same as NOT A AND NOT B

double negation

• if you reverse something twice you end up where you started

• NOT NOT A is equivalent to A

• ¬(¬A) = A

association

• allows us to remove brackets from an expression and regroup variables

• OR association rule

  • A V (B V C) = ( A V B) V C = A V B V C

• AND association rule

  • A ∧ (B ∧ C) = ( A ∧ B) ∧ C = A ∧ B ∧ C

commutation

• the order of the application of two separate terms is not important

• OR commutation rule

  • A V B = B V A

• AND commutation rule

  • A ∧ B = B ∧ A

distribution

• allows us to multiple of factor out an expression

• OR distribution rule

  • A ∧ (B V C) = (A ∧ B) V (A ∧ C)

• AND distribution rule

  • A V (B ∧ C) = (A V B) ∧ (A V C)

D-type flip flop

• a type of logic circuit which can store the value of one bit and flip it between 0 and 1 - used in memory circuits

• a flip flop has two inputs

  • single bit data input (D)

  • clock signal (C)

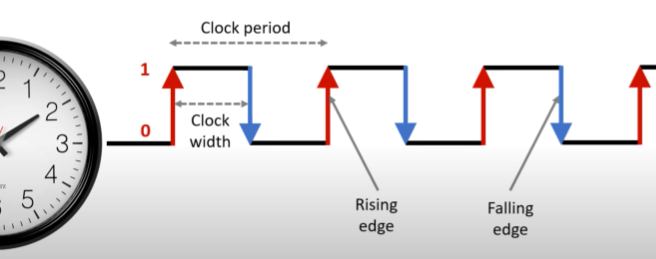
• a clock is a regular pulse generates by the CPU which is used to coordinate the computers components

• a clock pulse rises and falls, with edges labelled rising or falling

• a flip flop has two outputs

  • single bit data output (Q)

  • inverse of the data output (¬Q)

• the output of a D-type flip flop can only change at a rising edge, the start of a clock tick

  • edge triggered, allowing synchronisation with other components

  • otherwise the output value us held and does not change

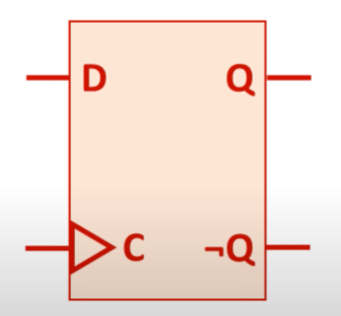
D-type flip flop clock

• a D-type flip flop is a positive-edge-triggered flip-flop

• this means the output can only be changed when the clock pulse is at a rising or positive edge (the moment the signal changes from low to high)

• if the clock is not at a rising or positive edge, the output value is held and does not change

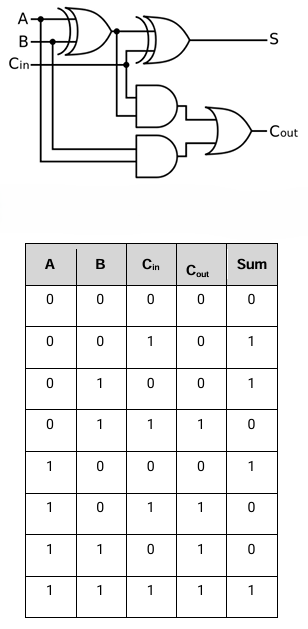
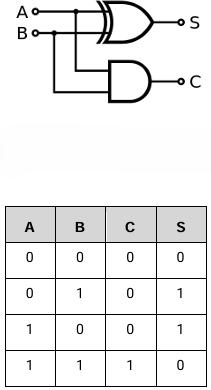
adders

a logic circuit which adds together the number of inputs which are true and outputs that number in binary

half adder

• has two inputs, A and B

• has two outputs, sum (S) and carry (C_out)

• the circuit is formed from an AND and XOR gate

• truth table, 4 rows

  • when A and B are both false - both outputs are false

  • when one of A or B is true, sum (S) is true

  • when both inputs are true, carry (C) is true

    • as in binary 1 + 1 = 0, carry the 1

full adder

• similar to a half adder but has three inputs, allowing for a carry in to be represented

• formed from two XOR, two AND gates and an OR gate

• truth table has 8 rows as apposed to 4 in the half adder

• because the full adder has a carry input, the circuits can be changed together

• how it works

• to add A, B and C_in together we use the first half adder to add A and B together - giving us X

• then use the second half adder to add the partial result, X to C_in - giving us the output, Digit

• finally one or both of the half adders may have generated a carry bit so this needs to be fed into the next calculation