A level Chem 1.5 Kinetics
1/14
Earn XP
Description and Tags
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
15 Terms
A mixture of 2 dm3 of hydrogen and 1 dm3 of oxygen is at room temperature.
Which statement is correct?
A There is no reaction to form water because the
molecules do not collide with sufficient energy.
B There is no reaction to form water because the
molecules do not collide with sufficient frequency.
C The mean velocity of the hydrogen molecules is less
than that of the oxygen molecules.
D The partial pressure of each gas is the same. (1)
A (1)
the activation energy for forming water is very high
Which statement is correct for the distribution curve of molecular energies in a gas?
A The curve is symmetrical about the maximum.
B There are always some molecules with zero energy.
C The position of the maximum of the curve is not
dependent on the temperature.
D The mean energy of the molecules is greater than the
most probable energy of the molecules
D (1)
higher because a few molecules have very high energy
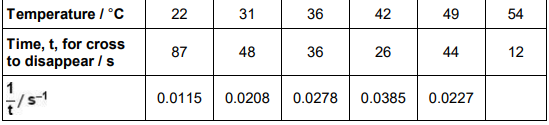
A student investigates the effect of temperature on the rate of reaction between sodium thiosulfate solution and dilute hydrochloric acid.
Na2S2O3(aq) + 2 HCl(aq) → 2 NaCl(aq) + SO2(g) + S(s) + H2O(l)
The student mixes the solutions together in a flask and places the flask on a piece of paper marked with a cross.
The student records the time for the cross to disappear. The cross disappears because the mixture becomes cloudy. The table shows the student’s results.
The student uses a stopwatch to measure the time. The stopwatch shows each time to the nearest 0.01 s Suggest why the student records the times to the nearest second and not to the nearest 0.01 s (1)
Idea that it is hard to judge to the nearest 0.01 second OR
Idea that it is hard to judge the exact moment (that it becomes too cloudy / the cross disappears)
OR
idea of reaction time (1)
A student investigates the effect of temperature on the rate of reaction between sodium thiosulfate solution and dilute hydrochloric acid.
Na2S2O3(aq) + 2 HCl(aq) → 2 NaCl(aq) + SO2(g) + S(s) + H2O(l)
The student mixes the solutions together in a flask and places the flask on a piece of paper marked with a cross.
The student could do the experiment at lower temperatures using an ice bath. Suggest why the student chose not to carry out experiments at temperatures in the range 1–10 °C (1)
Reaction would be too slow (1)
Iodide ions are oxidised to iodine by hydrogen peroxide in acidic conditions.
H2O2(aq) + 2H+ (aq) + 2I– (aq) → I2(aq) + 2H2O(l)
The rate equation for this reaction can be written as rate = k [H2O2] a [I–] b [H+]c
In an experiment to determine the order with respect to H+ (aq), a reaction mixture is made containing H+ (aq) with a concentration of 0.500 mol dm–3 A large excess of both H2O2 and I– is used in this reaction mixture so that the rate equation can be simplified to
rate = k1 [H+] c
Explain why the use of a large excess of H2O2 and I– means that the rate of reaction at a fixed temperature depends only on the concentration of H+ (aq). (2)
H2O2 and/or I– concentration (effectively) constant (1)
Only the concentration of H+ changes
so have a constant/no effect on the rate (1)
Iodide ions are oxidised to iodine by hydrogen peroxide in acidic conditions.
H2O2(aq) + 2H+ (aq) + 2I– (aq) → I2(aq) + 2H2O(l)
The rate equation for this reaction can be written as rate = k [H2O2] a [I–] b [H+]c
In an experiment to determine the order with respect to H+ (aq), a reaction mixture is made containing H+ (aq) with a concentration of 0.500 mol dm–3 A large excess of both H2O2 and I– is used in this reaction mixture so that the rate equation can be simplified to
rate = k1 [H+] c
Samples of the reaction mixture are removed at timed intervals and titrated with alkali to determine the concentration of H+ (aq). State and explain what must be done to each sample before it is titrated with alkali.(2)
Stop the reaction (1)
By dilution / cooling / adding a reagent to react with H2O2 /I–(1)
Explain the effect that lowering the temperature would have on the rate of reaction. (2)
Rate of reaction decreases
Fewer particles will have energy greater than or equal to the activation energy (1)
Fewer successful collisions in a given time (1)
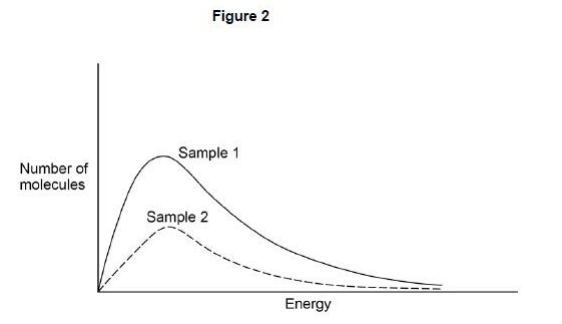
A Maxwell–Boltzmann distribution curve was drawn for a second sample of the reaction mixture in the same reaction vessel. Figure 2 shows the results.
Deduce the change that was made to the reaction conditions. Explain the effect that this change has on the rate of reaction.(3)
The amount of gas present (or number of molecules) has been reduced (1)
Rate of reaction decreases
Particles are spread further apart (1)
Fewer collisions between gas particles so fewer successful collisions (1)
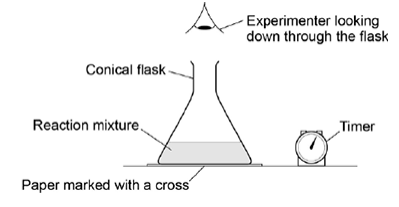
The apparatus in the figure below was set up to measure the time taken for 20.0 cm3 of sodium thiosulfate solution to react with 5.0 cm3 of hydrochloric acid in a 100 cm3 conical flask at 20 °C.
The timer was started when the sodium thiosulfate solution was added to the acid in the flask. The timer was stopped when it was no longer possible to see the cross on the paper.
What is likely to decrease the accuracy of the experiment ?
A Rinsing the flask with acid before each new experiment.
B Stirring the solution throughout each experiment.
C Using the same piece of paper for each experiment.
D Using different measuring cylinders to measure the volumes of acid and sodium thiosulfate. (1)
A (1)
If the flask is rinsed with acid, drops of acid remain inside.
When you add the sodium thiosulfate, the reaction starts early, before the timing begins.
The experiment was repeated at 20 °C using a 250 cm3 conical flask.
Which statement is correct about the time taken for the cross to disappear when using the larger conical flask?
A The time taken will not be affected by using the larger conical flask.
B The time taken will be decreased by using the larger conical flask.
C The time taken will be increased by using the larger conical flask.
D It is impossible to predict how the time taken will be affected by using the larger conical flask.
(1)
C (1)
That cloudiness takes longer to build up to the same density in the whole viewing path
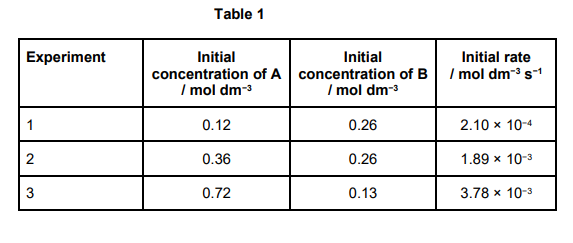
This question involves the use of kinetic data to deduce the order of a reaction and calculate a value for a rate constant.
The data in Table 1 were obtained in a series of experiments on the rate of the reaction between compounds A and B at a constant temperature.
Show how these data can be used to deduce the rate expression for the reaction between A and B. (3)
Consider experiments 1 and 2: [B constant]
[A] increases × 3: rate increases by 32 therefore 2nd order with respect to A (1)
Consider experiments 2 and 3 :
[A] increases × 2: rate should increase × 22 but only increases × 2
Therefore, halving [B] halves rate and so 1st order with respect to B (1)
Rate equation: rate = k[A]2[B] (1)
The rate equation for a reaction is
rate = k[E]
Explain qualitatively why doubling the temperature has a much greater effect on the rate of the reaction than doubling the concentration of E. (3)
Reaction occurs when molecules have more energy than activation energy/ E>Ea(1)
Doubling T by 10 °C causes many more molecules to have this E(1)
Whereas doubling [E] only doubles the number with this E (1)
A slow reaction has a rate constant k = 6.51 × 10−3 mol−1dm3 at 300 K.
Use the equation ln k = ln A – Ea / RT to calculate a value, in kJ mol−1 , for the activation energy of this reaction.
The constant A = 2.57 × 1010 mol−1dm3 .
The gas constant R = 8.31 J K−1mol−1 . (2)
Ea = RT(lnA – lnk) / 100 (1)
Ea = 8.31 × 300 (23.97 – (–5.03)) / 1000 = 72.3 (kJ mol-1) (1)
Draw the Maxwell–Boltzmann distribution curves for a fixed mass of a gas at two different temperatures.
This gas decomposes when heated.
By reference to these distribution curves, explain why the rate of decomposition of this gas increases at higher temperatures.(6)
Stage 1 - Single distribution curve
1a suitable axis labels:
vertical: number/proportion/fraction of molecules/particles; horizontal: (kinetic) energy
1b suitable shape (including on LHS must start
reasonably close to 0,0 and RHS must not meet x-axis or rise upwards (on each curve drawn))
Stage 2 - Distribution curve at higher temperature
2a peak moves to the right and down
2b area under the curve (roughly) the same
2c lines cross once only
Stage 3 - Why a gas reacts faster at higher temperature
3a molecules have more energy
3b more molecules have the activation energy
3c higher proportion of collisions are successful /
increases frequency of successful collisions
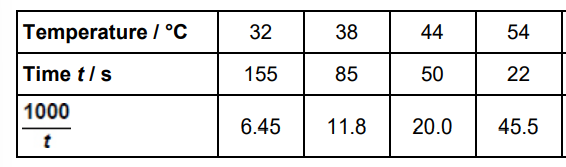
This question is about rates of reaction. Potassium manganate(VII), KMnO4, reacts with sodium ethanedioate, Na2C2O4, in the presence of dilute sulfuric acid.
2 MnO4–(aq) + 16 H+(aq) + 5 C2O42–(aq) → 2 Mn2+(aq) + 8 H2O(l) + 10 CO2(g) The reaction mixture is purple at the start and goes colourless when all the MnO4–(aq) ions have reacted
A student investigated how long it takes for this reaction mixture to go colourless at different temperatures. The same concentrations and volumes of each reagent were used in an experiment at each temperature. The table below shows the results
The student noticed that the temperature of each reaction mixture decreased during each experiment. Suggest how the student calculated the temperature values in the table above. (1)
Measure the temperature at the start and end of the reaction and find the mean/average (1)