Ch6 quality control and six sigma

SQC = statistical quality control

= setof tools used to evaluate organizational quality

• descriptive statistics

• statistical process control

• acceptance sampling

SQC : descriptive statistics

describe quality characteristics and relationships

SQC : statistical process control

inspect a random sample to decide whether a process is functioning properly

SQC ; acceptance sampling

inspect a random sample to decide whether to accept an entire lot

sources of variation

variation leads to quality defects and product inconsistency

common or random causes

• unavoidable due to slight differences in processing

• important to determine the range of natural random variation

assignable causes :

• can be identified and eliminated

• examples : defective machine, low quality materials, unexperienced workder

mean(x)

measures central tendency of a set of data

standard deviation

measures amount of data disperion around the mean

range (R)

measures the difference between the largest and smallest observation in the set of data

statistical process control

monitors the production process to make sure that it stays within the range of common variation

control chart

checks whether a sample of data falls within the control limits that separate common and assignable variation

control limits are usually set at 3 standard deviations from the mean → captures 99.47% of the normal variation

statistical process control : type 1 error

chance of detecting assignable variation when it does not exist (alpha)

statistical process control : type II error

chance of not detecting assignable variation when it exists (beta)

which charts can we use for variables

(values that can be measured on a continuous scale)

→ combination of X chart and R chart

which charts can we use for attributes

discrete values that can be counted (incl yes or no decisions)

use either P-chart or C-chart

control charts for attributes : P-chart

observations belong to either of two groups (ex product is accepatble or not)

total sample size is known → proportion of defects can be computed

control charts for attributes : c-chart

defects are counted per unit, but proportion of defecta can not be computed → example : number of complaints at a hotel

control VS capacity

process control : does the process fall within ranges of common variation

process capability : does the process meet it’s predefined tolerances (specifiaction limits) imposed by design specialists

→ a process must be both in control and capable

six sigma quality

Motorola (1980s)

ensures that mu falls +-6sigma falls within speciifcation limits

only 3.4 ppm instead of 2600ppm are defective

six sigma quality requires

technical tools : statistical quality control and problem solving tools

people involvement : training and responsibility

acceptance sampling

• randomly inspecting a number of items form a lot to decide whether the entire lot is accepted

• before or after (not during) the production process

• → typically if testing every item is too expensive or impossible destructive testing)

Operating Characteristics Curve

shows the discriminating power of a sampling plan

→ steeper : better

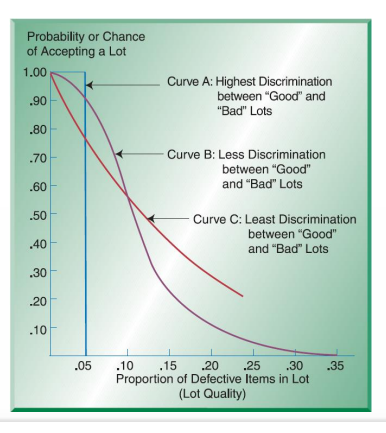
Operating Characteristics Curve : acceptable quality level AQL

small percentage of defects that customers are willing to accept

Operating Characteristics Curve : lot tolerance percent defective LTPD

maximum percentage of defective items in a lot that customers tolerate

Operating Characteristics Curve : consumer risk (type II error)

chance of accepting a lot that contains more that LTPD defects

Operating Characteristics Curve : producer risk (Type I error)

chane of rejecting a lot that contains less than AQL defects

acceptance sampling : average outgoing quality AOQ

expected proportion of defective items passed to the customer

AOQ is typically low for very good and very bad lots, but higher in between