Abstract Algebra

Vocabulary, Concepts, & Definitions

Group

Set with a binary operation that is associative, contains a neutral element, and every element in the set has an inverse element in the set under the binary operation. The set is closed under its binary operation.

Ring

Set with two binary operations, denoted by addition and multiplication. Both are associative. The set forms a commutative group under addition. The distributive property must hold between addition and multiplication. The set must be closed under both operations.

Unity

In a ring, unity refers to the multiplicative neutral. It is denoted 1R. A ring that contains a unity is known as a ring with unity.

Commutative Ring

A ring in which the multiplicative operation is commutative. Thus, both the operations are commutative.

Bijection

A function or map that is both injective and surjective.

Injective

1-1; every output has a unique input so that none of the inputs share outputs. Thus if f(a)=f(b), then a=b.

Surjective

onto; every element in the codomain is also in the range, for every element in the codomain has at lease one element in the domain that maps to it.

Group Homomorphism

A map between two groups (designated phi) that respects the group operation by fulfilling the following property

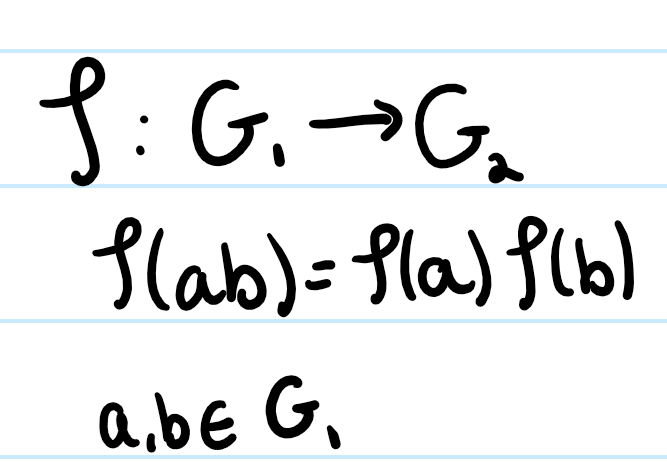
Group Isomorphism

A bijective group homomorphism. Every element in one group can be assigned to an unique element in the other group and the structure of the two groups are the same. The Cayley diagram of one group should match the Cayley diagram of the other group so that the points are just relabeled.

Cosets

A set that can be computed by composing every element of a subgroup by an element in the group. Right cosets are found by composing the new element on the right of the subgroup and left cosets are found by composing the new element on the left of the subgroup.

Subgroup

A subset of another group that also forms a group. All elements in the subset must also be elements of the group, the subset must contain the neutral element, every element in the subset must have its inverse in the subset, composing two elements in the subset produces another element in the subset (closure).

Normal Subgroup

A subgroup whose left and right cosets are equivalent.

Center

Z(G); The set of elements in a group that commute with all elements in a group.

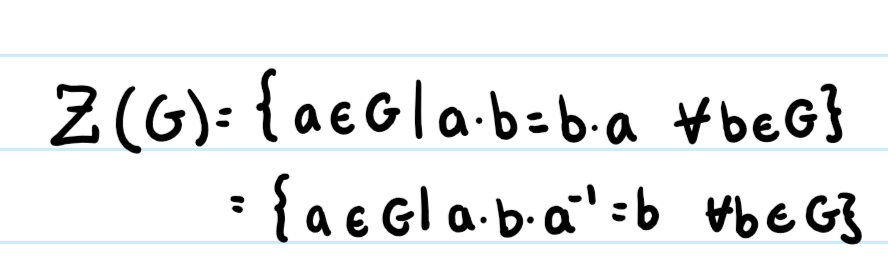
Automorphism

An isomorphism from a group to itself. Can be found by mapping generators of the group to all other generators of the group.

Abelian

Another term for commutative

Commutative

a*b=b*a

Associative

a*(b*c)=(a*b)*c

Kernel

The preimage of e₂ in G₁. All the elements in G₁ that map to the identity in G₂. The kernel always forms a subgroup in G₁. It is often denoted by the letter K.

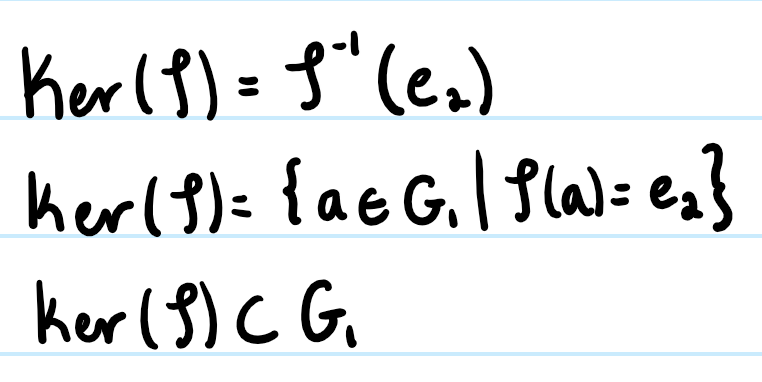
Conjugated

Two elements, a and b in G, are conjugated if there exists an element c in G, such that ac=cb or a=cbc^-1. Conjugation defines an equivalence relation: x~y iff x=zyz^-1 for some z in G.

Cyclic

A group is considered to be cyclic if all the elements in the group can be generated by a single element. All subgroups of a cyclic group are cyclic. All cyclic groups are isomorphic to Z_n where n is the number of elements in, or the order of, the cyclic group in question.

Equivalence Relation

An equivalence relations relates two elements in a set, a and b, written as a~b, and fulfills the following properties: Reflexivity, Symmetry, and Transitivity. Every equivalence relation determines a partition of a set.

Partition

All elements of a set are included in a single grouping and no elements can appear in multiple groupings. A partition is also known as a disjoint union of a set.

Reflexivity

a~a (or a=a depending on notation)

Transitivity

If a~b and b~c, then a~c

Equivalence Class

In a group, a subset of elements that are all equivalent to each other based on a given equivalence relation.

Group Action

A group homomorphism from a group G on a set X. It is generally denoted rah. Every element in the set is mapped to another element in X. Essentially the group maps the set X to permutations of X.

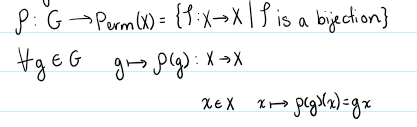
Orbit

The orbit (x) is all of the elements that x can be mapped to in the set using the group operation. All of the potential images of x in the set. A subset of X.

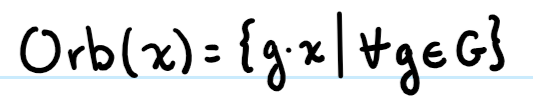
Stabilizer

The stabilizer of x is all of the elements in G that map x to itself using the group operation (or group action). The stabilizer is a subgroup of G.

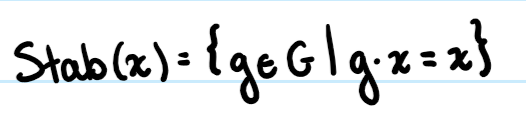
Orbit-Stabilizer Theorem

For any group action, the Order of G is equal to the order of the stabilizer of a particular element multiplied by the order of the orbit for that same element.

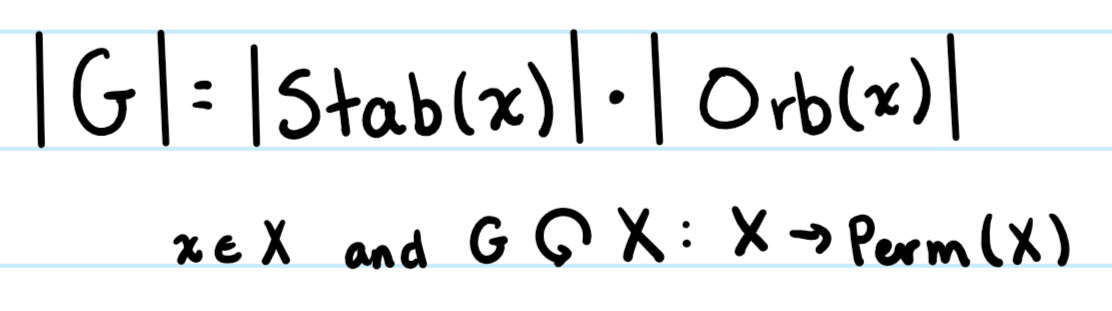
Innerautomorphisms

A special type of automorphism that is given by the conjugation action. Innerautomorphisms map elements within their conjugacy classes.

Cayley Table

Describes the structure of a finite group by arranging all possible products of all the group’s elements in a table similar to that of an addition or multiplication table. A Cayley table is able to tell us if the group is abelian, the inverses of each element, and the center.

Cayley Diagram

Also known as a Cayley graph. It encodes the abstract structure of a group. It uses a specified set of generators for the group.

Unit

In a ring, a unit is an element with a multiplicative inverse

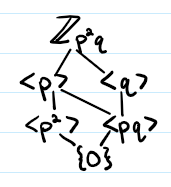
Lattice of Subgroups

A vertical diagram of all subgroups of a group that shows the structure of the subgroups, i.e. which subgroups are a subgroup of other subgroups.

Lagrange’s Theorem

For any finite group, G, the order of a subgroup of G, H, divides the order of G

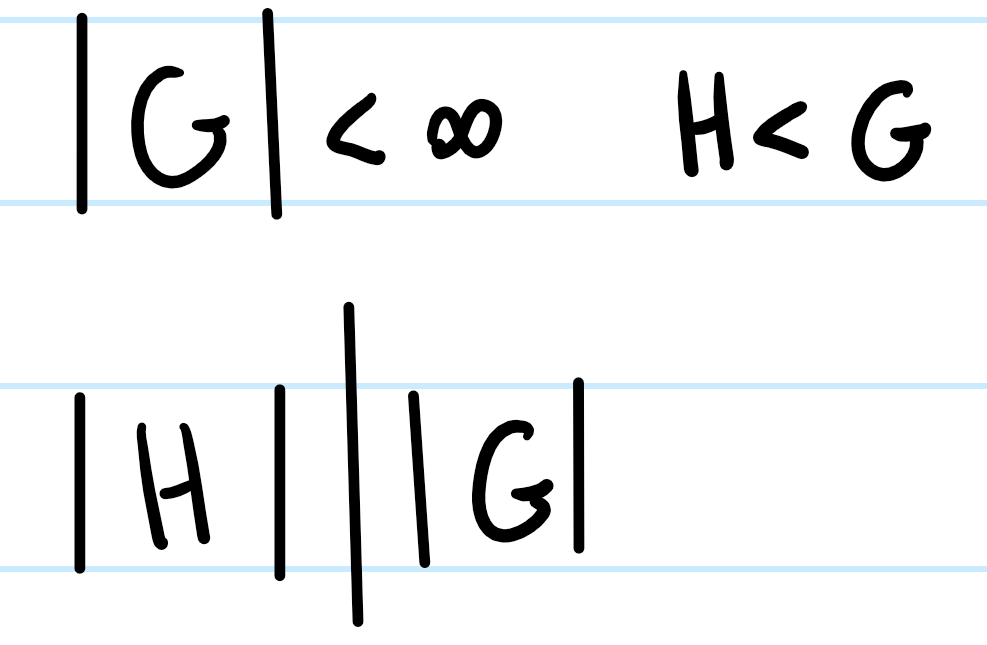
Permutation

Let X be a set. A permutation of X is a bijection f: X → X. All of the ways to arrange the set.

Order of Permutations

The least common multiple of the order of each disjoint cycles.

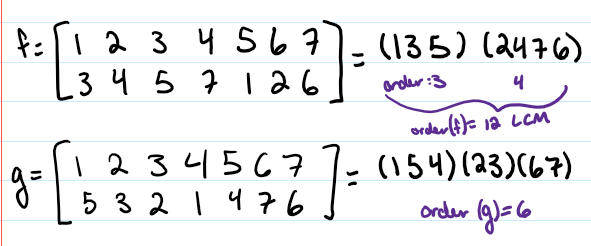
Even Permutations

If the permutation can be written as an even number of transitions, it is an even permutation.

Odd Permutations

If the permutation can be written as an odd number of transpositions, it is an odd permutation.

Transposition

Also known as a disorder. A 2 cycle. A permutation of only two elements. Every permutation can be written as a product of transpositions.

Prove the following implication.

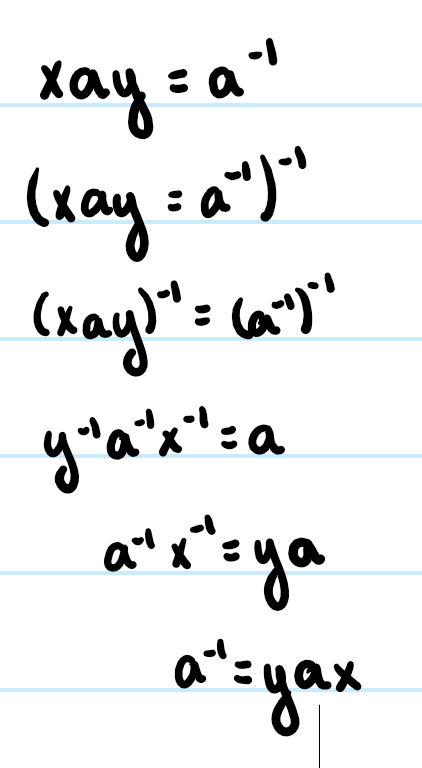
Prove the following implication.

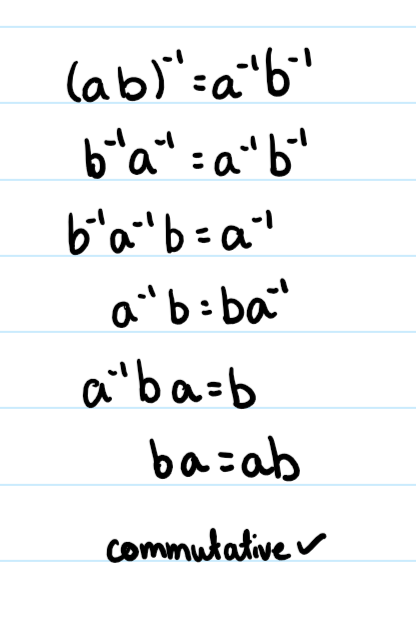
Quotient Group

Also known as a factor group. A group whose elements are equivalence classes that is found by moding out by a normal subgroup. It is the set of cosets of the subgroup that you mod out by.

Symmetry

If a~b, then b~a

Well Defined

When working with an operation of equivalence classes, the operation is “well-defined” if it does not matter which representative that we choose from the equivalence class. I.e., when adding fractions, it is well defined because we can replace ½ with 3/6 and the result is equivalent.

---

Centralizer

The set of elements in a group which commute with all elements in the group. It is a subgroup of G.

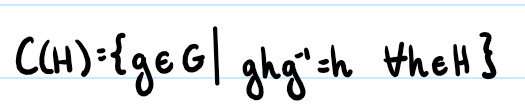
Normalizer

The set of elements in a group that permute with a particular subset.

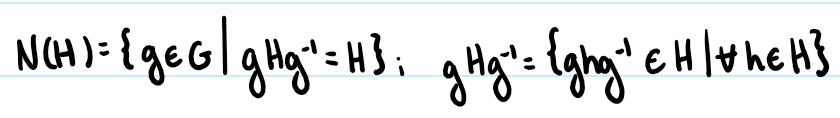
Subring

A subset of a ring with the same two binary operations that fulfills all of the requirements to be a ring.

Ideal

A subring, I, of a ring, R, where multiplying any element in the subring by an element in the ring produces an element in the subring. When multiplication is commutative, it is a two-sided ideal. Otherwise, you have right ideals and left ideals.

Distributive Property

a(b+c) =ab+ac

Field

A commutative ring with unity in which there are no non-zero zero divisors. This means that every element, excluding zero, has a multiplicative inverse.

Integral Domain

A commutative ring in which there are no non-zero zero divisors.

Quotient Ring

Similar to a quotient group, it is a ring whose elements are equivalence classes that is found by moding out by an ideal.

Linear Comination

An expression constructed from a set of terms by multiplying each term by a constant and adding the results. An example is a₁v₁+a₂v₂+…+a_nv_n

Ring Homomorphism

Similar to a group homomorphism but working with rings.

Kernel of Ring

Similar to the kernel of a group. All the elements in R₁ that map to the additive identify in R₂

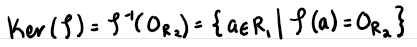
Principal Ideal

An ideal that can be generated by a single element

Irreducible

An element q is irreducible if it is non-zero and not a unit and fulfills the following property: if q=a * b, then either a is a unit or b is a unit

Prime

An element p is prime if p is non-zero and not a unit and fulfills the following property: if p divides ab, then p divides a or p divides b

Euclidean Domain

A ring in which the Euclidean algorithm holds. A subset of integral domains in which we can do long division. There must exist a “size” function to determine if one element is “smaller” than another (absolute value in integers, order of polynomials)

Euclidean Algorithm

The process to determine the GCD of two elements.

Maximal Ideal

An ideal in which there is no other ideals that can be squeezed between the ideal and the ring. Maximal ideals are generated by an irreducible element.

Prime Ideal

An ideal in which every element of the ideal is prime.

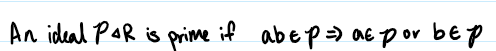
Characteristic of a Ring

In a ring with unity, the characteristic of the ring is the number of times that the multiplicative identity is added to itself to produce the additive neutral.

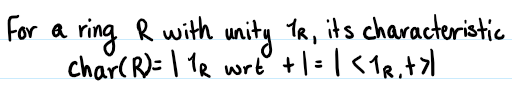
Rational Root Theorem

For any polynomial p(x) with integer coefficients, p(x)=a_kx^k+…a₁x+a₀ and q=n/m is a rational number and a root of p(x), then m divides a_k and n divides a₀

Field Expansion

Adding additional values to a field by solving a polynomial equation that does not have a rational root by moding out by an irreducible polynomial.

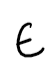
“is an element of”

When related to subgroups

“is a normal subgroup of”

When related to rings

“is a two-sided ideal of”

When related to groups

“is a subgroup of”

When related to rings

“is a subring of”

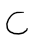
“is a subset of”

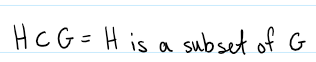
The set of all integers; {…,-2, -1, 0, 1, 2, …}

The set of all rational numbers; the set of all elements that can be written as the ratio of two integers, a set of equivalence classes

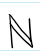
The set of all natural numbers; normally {1, 2, 3, …} but Anton includes 0

The set of all complex numbers; any real number can be written as a complex number with the “i” term having a coefficient of 0

“for any”/”for all”/”for every”

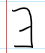
“there exists”

s.t.

“such that”

w.r.t.

“with respect to”

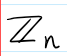
The group of integers under addition mod n

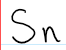
The set of all possible permutations of n elements

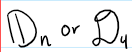
The set of symmetries of an equilateral 2D figure with n sides; D₄ is the group of symmetries of a square

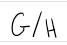
Quotient group found by moding out by H in G; the set of all cosets of H (where H must be a subgroup of G

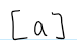
The equivalence class of a; the set of all elements equivalent to a under the given equivalence relation

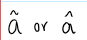
A way to differentiate from a variable name we already used

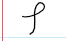
Phi; used to denote a group homomorphism

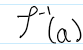
The preimage of Phi(a); All of the elements in G₁ that map to a in G₂

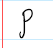
Rha; used to denote a group action

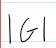
Order of G; the number of elements in G

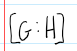
The index of H in G; the number of distinct cosets of H in G

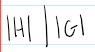
The order of H divides the order of G; the order of H is a factor of the order of G

Disjoint union; combine two sets but do not repeat shared elements

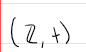
(set, operation); In this case, the set of integers under addition

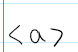
The set generated by a

Action; denotes a group acting on a set

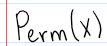
Permutations of a set X

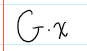
Orbit of x in G

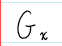
Stabilizer of x in G

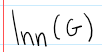
Symmetries of automorphisms; the set of innerautomorphisms of G