Applications of Differentiation

What is Rolle’s Theorem?

Suppose f : [a, b] → R is continuous on [a, b], differentiable on (a, b), and f(a) = f(b). Then there exists a c in (a, b) such that f’(c) = 0

What is the Mean Value Theorem?

Suppose f : [a, b] → R is continuous on [a, b] and differentiable on (a, b). Then there exists a c in (a, b) such that (f(b) - f(a))/(b - a) = f’(c). (Useful for proving inequalities of the form |f(x) - f(y)| \< c|x - y|)

How to tell if a function is constant, increasing or decreasing?

Suppose f : [a, b] → R is continuous on [a, b] and differentiable on (a, b).

• If f’(x) = 0, f is constant

• If f’(x) > 0, f is strictly increasing

• If f’(x) < 0, f is strictly decreasing

What is the Generalised Mean Value Theorem?

Suppose f : [a, b] → R is continuous on [a, b], differentiable on (a, b), and that g’(x) =/ 0 for every x in (a, b). Then there exists a c in (a, b) such that (f(b) - f(a))/(g(b) - g(a)) = f’(c)/g’(c)

What is L’Hôpital’s Rule?

lim_x→x0f(x)/g(x) = lim_x→x0f’(x)/g’(x) provided that lim_x→x0f(x) = lim_x→x0g(x) = 0 or lim_x→x0f(x) = lim_x→x0g(x) = infinity (indeterminate form)

What does it mean if a function is infinitely differentiable?

If the nth derivative, f⁽ⁿ⁾ exists for all positive integers n

What is the Taylor polynomial?

Taylor series centered at 0 are usually known as Maclaurin series

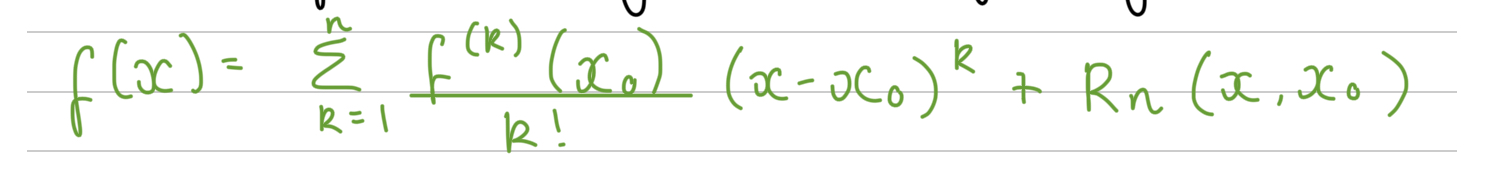
What is the formula for the error term in the Taylor polynomial?

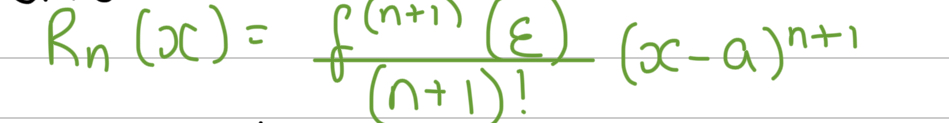
What is the Maclaurin series formula?

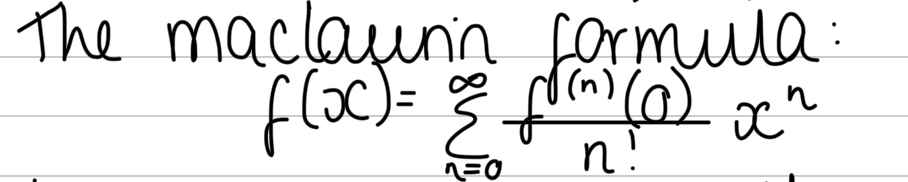
Let c belong to Dom(f) for a real function f. What is the absolute min and max of f?

• f(c) is the absolute min of f on Dom(f) if f(c) \< f(x) for all x in Dom(f)

• f(c) is the absolute max of f on Dom(f) if f(c) >/ f(x) for all x in Dom(f)

What are the max and min values of a function f called?

Extreme values

What are absolute min and max values sometimes called?

Global min and max

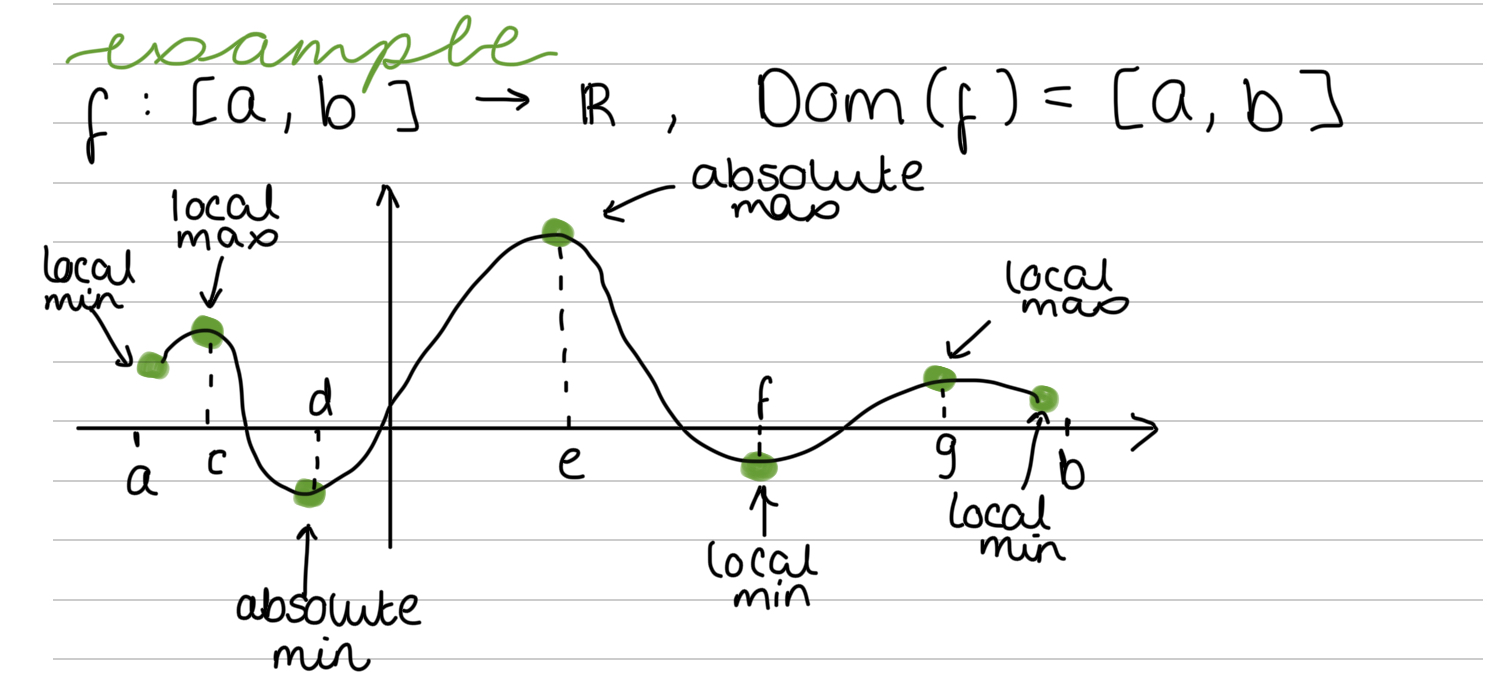
Let c belong to Dom(f) for a real function f. What is the local min and max of f?

• f(c) is the local max value of f if f(c) >/ f(x) for all x close to c (i.e. there exists a δ > 0 such that f(c) >/ f(x) for every x belonging to (c - δ, c + δ) and in Dom(f))

• f(c) is the local min value of f if f(c) \< f(x) for all x close to c (i.e. there exists a δ > 0 such that f(c) \< f(x) for every x belonging to (c - δ, c + δ) and in Dom(f))

What is Fermat’s Theorem?

If f has a local max/min at c belonging to (a, b)and f’(c) exists then f’(c) = 0

What is a critical point?

The number c in Dom(f) such that f’(c) = 0 or f’(c) DNE

What are the steps to finding the max/min points of a function?

1. Find values at critical points

2. Find values at endpoints

3. Pick the largest/smallest values from above

What is the derivate test for extreme values?

• If f’(x) > 0 for x < c and f’(x) < 0 for x > c then f(c) is a maximum of f

• If f’(x) < 0 for x < c and f’(x) >0 for x > c then f(c) is a minimum of f

What is the definition of a horizontal asymptote of the curve y = f(x)?

The line y = L is called a horizontal asymptote if either lim_x→∞f(x) = L or lim_x→-∞f(x) = L

What is the definition of a vertical asymptote of the curve y = f(x)?

The line x = a is a vertical asymptote if at least one of the following is true: lim_x→a⁺f(x) = ∞, lim_x→a⁺f(x) = -∞, lim_x→a^-f(x) = ∞ or lim_x→a^-f(x) = -∞

How to tell if a curve is concave upward?

f”(x) > 0

How to tell if a curve is concave downward?

f”(x) < 0

What is an inflection point?

Where a curve changes concavities

What are the steps for sketching a curve?

1. Determine domain of f using domain convention

2. Find intersections with axis (f(0), f(x) = 0)

3. Symmetry and whether it is an odd or even function

4. On which intervals it is increasing/decreasing (f’(x) > 0, f’(x) < 0)

5. Local max/mins

6. Concavity and inflection points

7. Asymptotes