2.3.2 algorithms for main data structures

stacks

• first in, last out (FILO) data structure

• they are often implemented as an array and use a single pointer which keeps track of the top of the stack (called the top pointer)

• this points to the element which is currently at the top of the stack

• the top pointer is initialised at -1; this is because the first element in the stack is in position 0, and having the top initialised at 0 would suggest there is an element in the stack, when in fact the stack is empty

stack operations

• size - checks the size

• isEmpty - checks if the stack is empty

• peek - return the top element without removing it

• push - add an element to the top of the stack

• pop - remove and return the top element from the stack

queue

• first in, first out (FIFO) data structure

• unlike stacks, queues make use of two pointers: front and back / head and tail

• while front holds the position of the first element, back stores the next available space

queue operations

• size - checks the size

• isEmpty - checks if the stack is empty

• peek - return the top element without removing it

• enqueue - add an element to the queue

• dequeue - remove and return element from the front of the queue

linked list

• data structure that provided a foundation upon which other structures can be built

• composed of nodes, each of which contains data has a pointer to the next item in the list

• circular linked list - last node points to first node

• items dont need to be stored contiguously due to pointers

trees

• formed from nodes and edges, which cannot contain cycles and aren’t directed

• trees are useful as a data structure because they can be traversed

• used for storing and managing file and folder structures

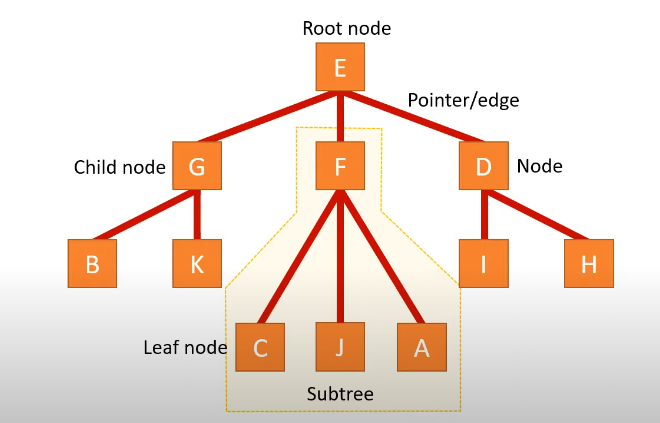
binary tree

similar to a standard tree but each node can only have 0, 1 or 2 pointers

adding to a binary tree

1. check if there is free memory

2. create a new node

3. if tree is empty, new node becomes the root, create a start pointer to it

4. if not, starting at the root node, check if the new value should be placed before or after the current node

5. before = left, after = right

6. continue until a leaf node is reached

7. find out if the new value comes before or after the leaf

8. set new pointer to the new value

removing from a binary tree

1. find node we want to delete

2. set that node as the current node

3. while the current node exists

   1. set the previous node the same as the current node

   2. check if item to be deleted is less or greater than the current node

   3. less = follow left pointer, right = follow right pointer

   4. back to stage 3

4. if the node being deleted is a leaf

   1. if its less than, previous nodes pointer = null

   2. if greater than, right pointer = null

5. if node being deleted has 1 child

   1. if less than, set the previous nodes left pointer to the current nodes left child

   2. if greater than, set right pointer to the current nodes right child

6. if the node being deleted has 2 children

7. replace it with the smallest value in the right sub-tree

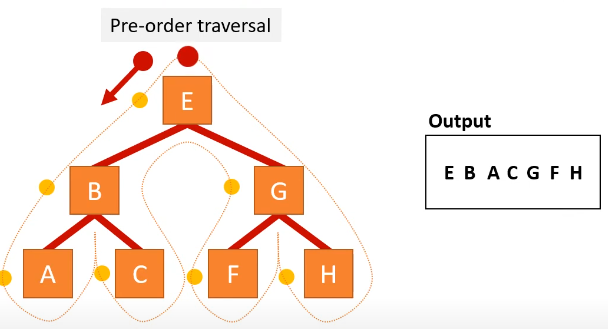
pre-order traversal

• node left right

• dot on left, start at root

• start at root

• output node

• follow left pointer and repeat step 2 until there is no pointer to follow

• follow right pointer and repeat step 2 until there is no pointer to follow

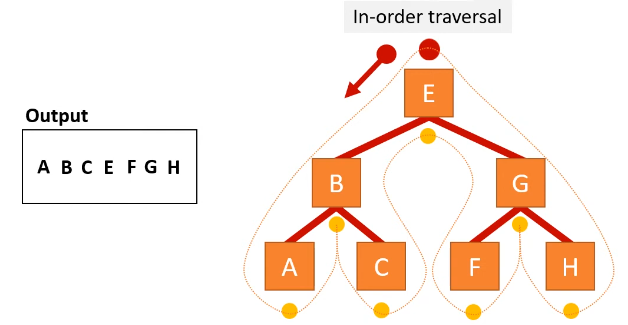
in-order traversal

• left node right

• dot on bottom, start on most left node

• start at toot node

• follow left pointer and repeat from step 2 until there is no pointer to follow

• output the node

• follow right pointer and repeat step 2 until there is no pointer to follow

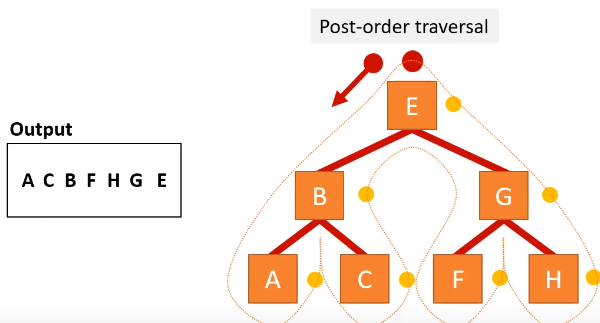
post order traversal

• left right node

• dot on right, start at furthest left node

• start at root node

• follow left pointer and repeat from step 2 until there is no pointer to follow

• follow right pointer and repeat step 2 until there is no pointer to follow

• output the node

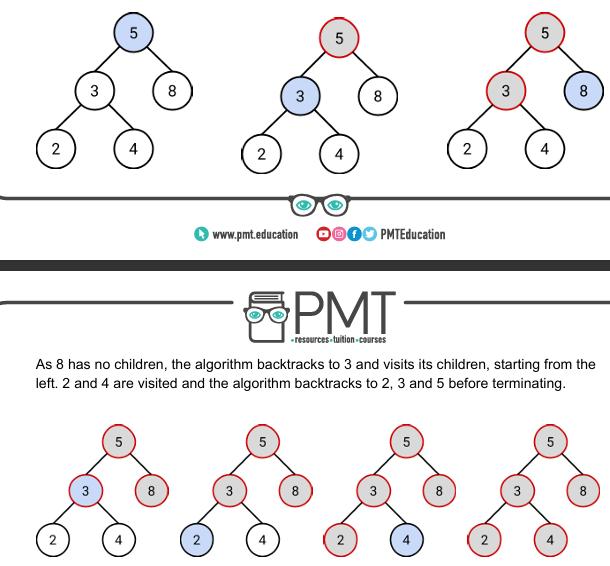
breadth first

• start from root, visit all the roots children starting from the left child

• the algorithm then visits all nodes directly connected to each of those nodes in turn, continuing until every node has been visited

• layer by layer