Population Growth

Chapter 4-7

Life Table

Summary of survival and reproduction across lifetime

• “Snapshot” of life history of a population

Life Table Y-Axis

Log Scale

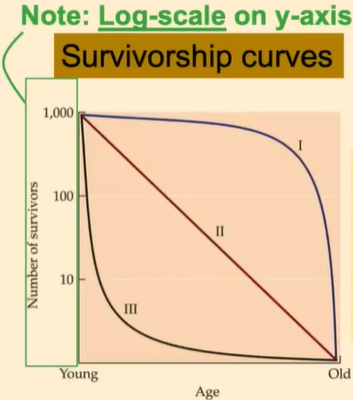
Type I Survivorship Curve

Lots of offspring live to old age

• Little predation

• Most mortality due to old age

Type II Survivorship Curve

Constant death rate across age

Type III Survivorship Curve

Lots of offspring die young

• Lots of predation

Population Size of Next Year

[# of Survivors] + [# of Births]

Stable Age Distribution

If survival and fecundity stay the same —> then population will reach a predictable age distribution (constant growth rate)

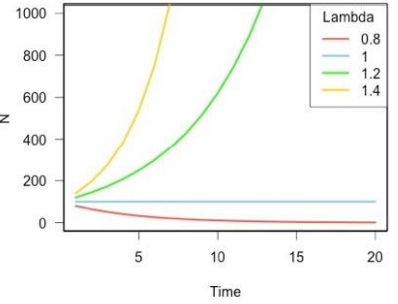
Exponential Population Growth

Same as geometric growth but for case where reproduction occurs continuously

The defining feature of geometric/exponential population growth is…

Population growth rate (λ or r) is constant across time, it does not change

If population size increases:

• dN/dt = increases

• r = no change

λ > 1 or r > 0

• Population growth rate is positive

• Population increases in size

λ < 1 or r < 0

• Population growth rate is negative

• Population decreases in size

λ = 1 or r = 0

• Population growth rate is 0

• Population size stays the same

Normal Scale

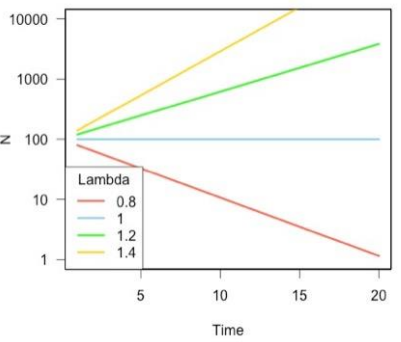
Log Scale

Density-Independent Factors

Effect on birth and death rates are independent of the number of individuals in the population

• Drought

• Extreme weather

• Flood

• Pollution

Density-Dependent Factors

Birth, death, and dispersal rates change as the density of the population changes

• Most often, there is negative density dependence (deaths increase when population is crowded)

What happens when you increase density, specifically the # of breeding females?

Reduces birth rate because of per capita resource abundance

• Can reverse by adding more resources

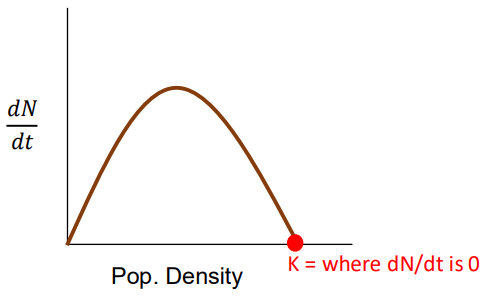
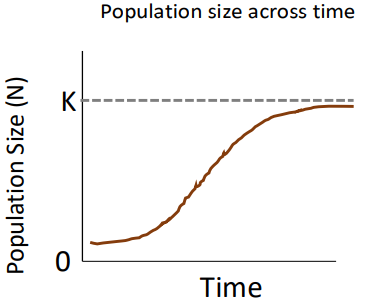
Logistic Growth

Population increases rapidly, then stabilizes at the carrying capacity (K)

K

Maximum population size that can be supported indefinitely by the environment

Carrying Capacity

Determined by the amount of resources

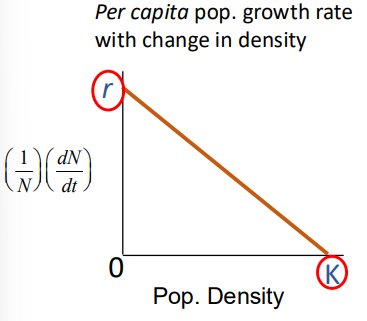
• Birth rate = Death rate

• Per-Capita growth rate = 0

When N is small relative to K (N < K)

Population growth almost like exponential growth

When N is close to K (N = K)

Population stops growing

What is the slope of the tangent line?

dN/dt or overall population growth rate

Logistic Growth: Population size across time

Logistic Growth: Per capita pop. growth rate with change in density

Logistic Growth: Population growth rate with change in density