Physics - Translational Motion

Kinematics, Newton's Laws, Free Body Diagrams, Work & Energy, Momentum & Impulse

Newton’s 1st Law

Inertia; objects in motion stay in motion

Fnet = 0 at equilibrium

Newton’s 2nd Law

F = ma

Newton’s 3rd Law

Equal and opposite reations

Fa:b = - Fb:a

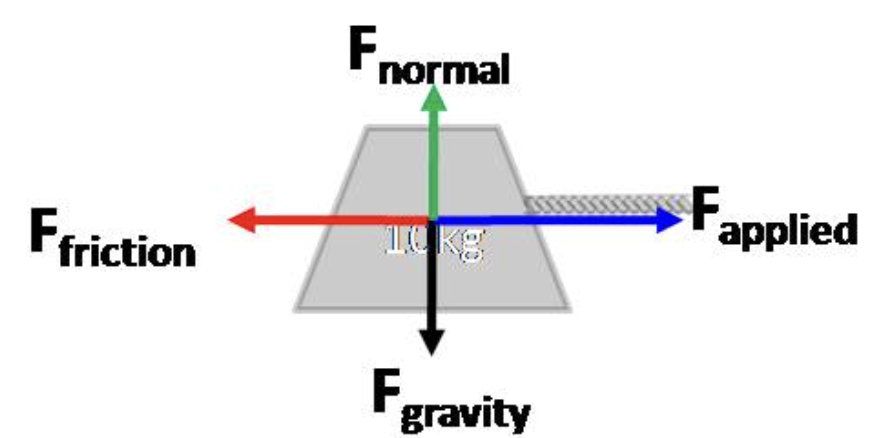
In a free body diagram on a flat surface FN (normal force) points:

Up

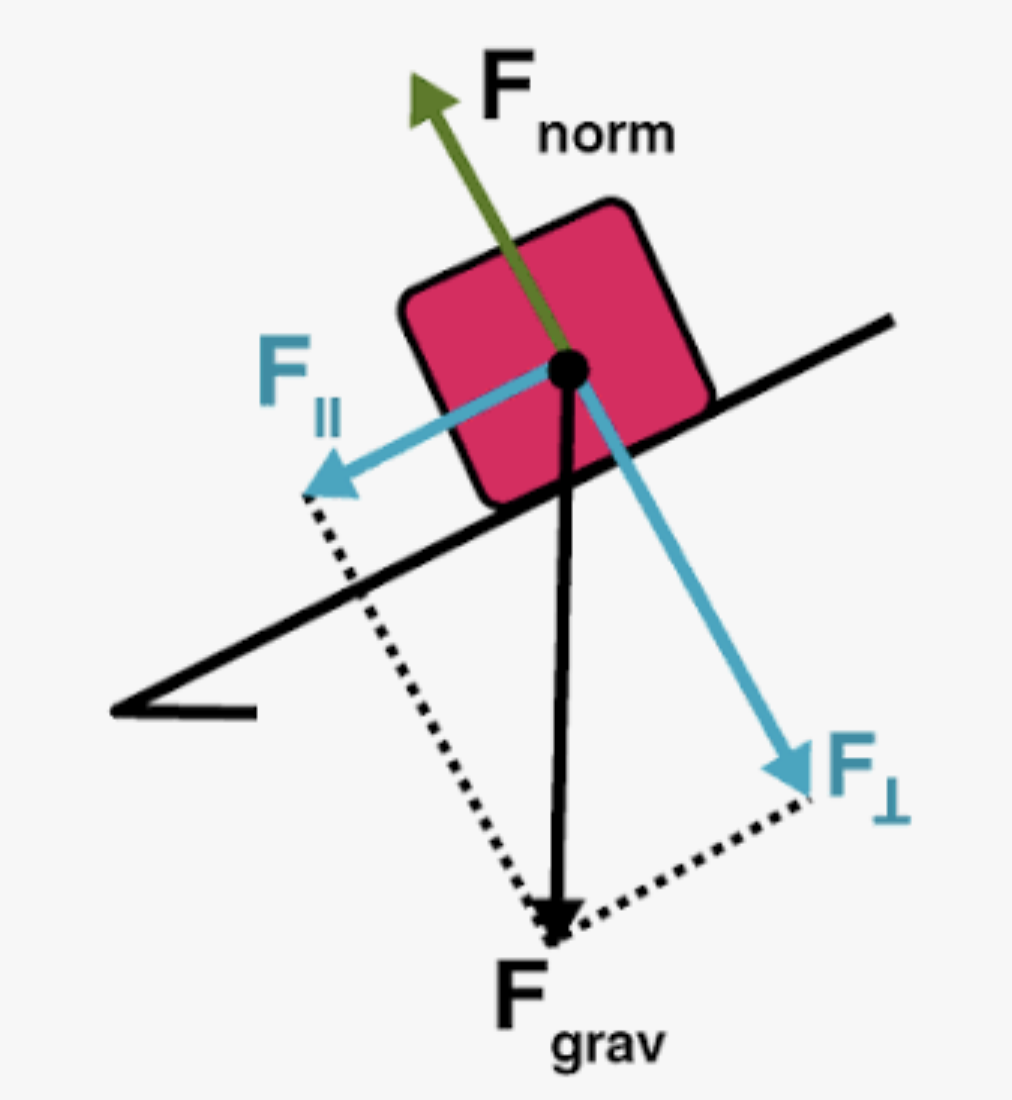
In a free body diagram on an incline plane FN (normal force) points:

Perpendicular to incline

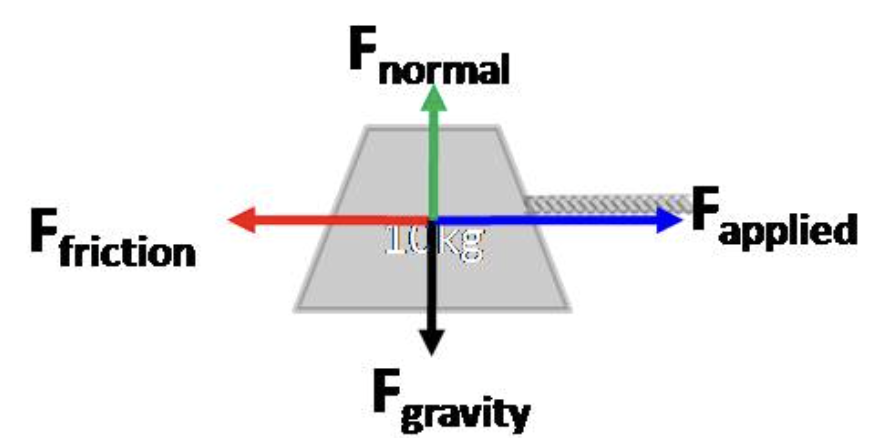
In a free body diagram on a flat surface Fg points:

Down

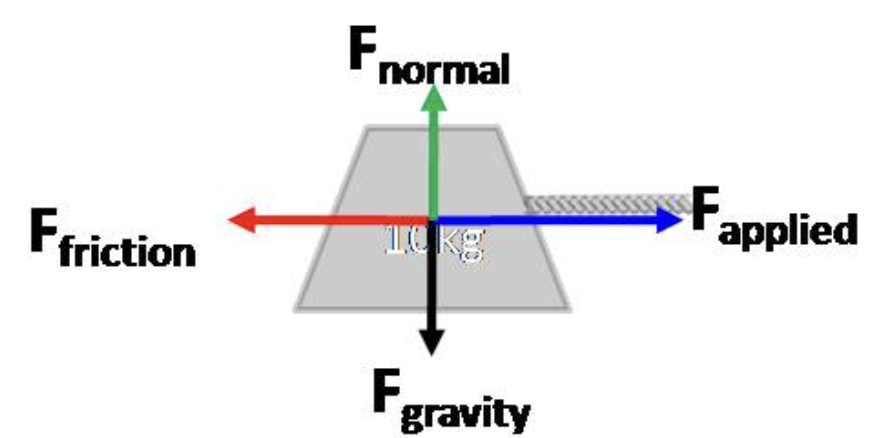
In a free body diagram on a flat surface Ff (friction force) points:

Opposite to the direction of applied force

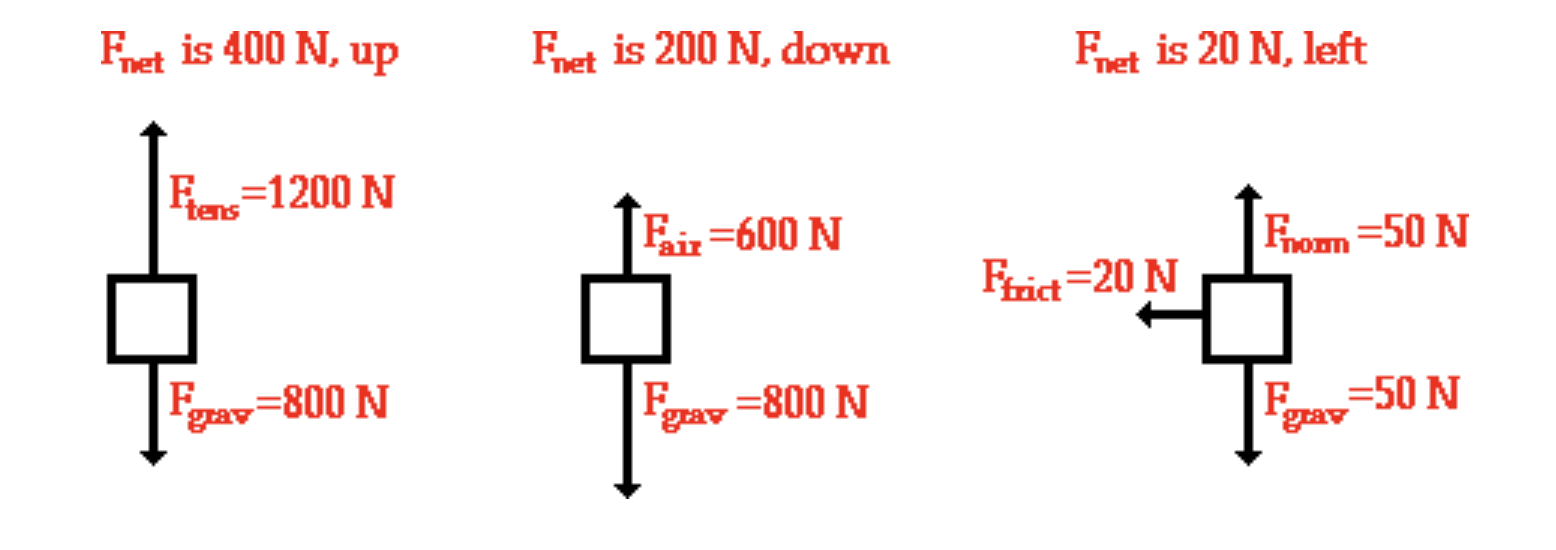
In a free body diagram the net force is:

The summation of all the forces acting on the object

When splitting into x and y components : the component adjacent to the angle uses : (sin or cos)

Cos

When splitting into x and y components : the component opposite to the angle uses : (sin or cos)

Sin

Change in position

Displacement

Change in displacement over time

Velocity

Change in velocity over time

Acceleration

Write the kinematic equations:

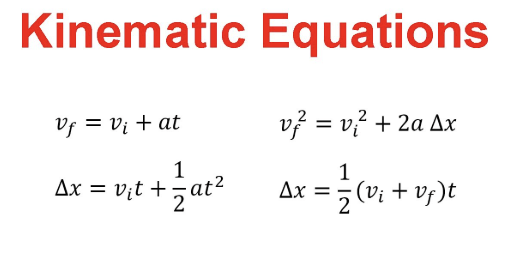
In linear motion and free fall, at the top of flight the instantaneous velocity =

0

In free fall and linear motion the time of the object going up =

the time of the object going down

In projectile motion the x-component a = __ ; v = __

0 ; vcos(theta)

In projectile motion the y-component a = __ ; v = __

g ; vsin(theta)

Kinetic energy =

½ mv²

Gravitational potential energy =

mgh

Spring potential energy =

½ kx²

Work =

Fdcos(theta)

Net Work =

Change in kinetic energy

Momentum p =

mv

Impulse J =

change in p or F * change in time

Torque =

rFsin(theta)