BIOL2300 ch. 1-5

statistics

the study of methods for measuring aspects of populations from samples and for quantifying the uncertainity of the measurements

population

all the individual units of interest

sample

subset of units taken from the population

parameter

true value that describes an entire population; absolute “truth”

estimate

an approximation of the parameter

always subject to error because it doesn’t include every individual in the population

random sample

each member of a population has an equal and independent chance of being selected

minimizes bias; makes it possible to calculate amount of sampling error

sample of convenience

a collection of individuals that are easily available to the researcher

sampling error

the natural, unavoidable difference (due to chance) between an estimate and the population parameter being estimated 

reducing sample size decreases precision

bias

a systematic discrepancy between the estimates

list 4 types of bias

1. volunteer bias

2. survivorship bias

3. recall bias

4. observer bias

accuracy

how close an estimate is to the true value (parameter)

precision

how consistent/reproducible measurements are from one sample/measurement to another 

sampling variability affects precision

categorical data

qualitative characteristics of individuals (non-numerical)

what are the 2 types of categorical data?

1. nominal

2. ordinal

nominal

no inherent order (categorical)

ordinal

inherent order (categorical)

numerical data

quantitative measurements (numerical values)

what are the 2 types of numerical data?

1. discrete

2. continuous

discrete, provide examples

indivisible units (numerical)

i.e. # of teeth; # of siblings; # of vehicles

continuous, provide examples

 any real number within a range (numerical)

i.e. height, weight, temperature

absolute frequency distribution (n)

the count of observations in each category/interval

example of absolute frequency distribution

Ex. absolute frequency of age surveyed across students in a class;
Age 19: 37 students
Age 22: 5 students

relative frequency distribution (f) or (p)

the proportion/percentage of observations in each category/interval

example of relative frequency distribution

Ex. relative frequency of age surveyed across students in a class

Age 19: 40.7% of students

Age 22: 5.5% of students

experimental study

researcher assigns treatments randomly

observational study

assignments not made by researcher

confounding variable

masks/distorts the causal relationship between measured variables in a study

example of confounding variable

E.x. Coffee consumption and the incidence of lung cancer (does not actually cause lung cancer, smoking does)

how should categorical data be displayed?

• frequency table

• bar graph

how should numerical data be displayed?

• frequency table

• box plot

• histogram

positive skew (right-skewed)

• mean > median

• long tail on right side

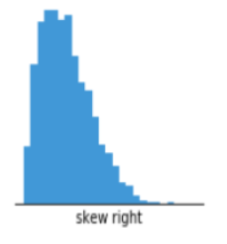
negative skew (left-skewed)

• mean < median

• long tail on left side

how should relative frequency be displayed?

• bar graph

• pie chart

what should be used to visualize the association between categorical variables and compare their frequencies?

contingency table

how should the association between categorical variables be displayed?

• grouped bar

• mosaic plot

how should the association between numerical variables be displayed? label the axes

scatter plot

• x-axis: explanatory variable

• y-axis: response variable

how should the association between categorical and numerical variables be displayed?

• strip chart

• violin plot

normal distribution (histogram)

symmetric bell-shaped distribution

• mean/median/mode are very similar

• does not show percentiles

mean

the average value; typical value

median

middle value when data is ordered least to greatest

standard deviation (SD)

how spread out the data is around the mean; spread of individual observations

• Never negative

• The sum is zero

• SD = Square root of variance

mode

value that appears most frequently in a data set

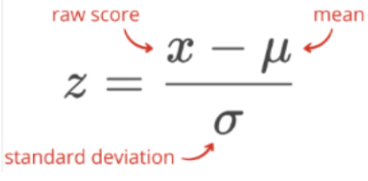
z-score

indicates how many standard deviation a value is above or below the mean

paired/dependent observations

data collected multiple times from the same individuals

positive association

two variables move in the same direction (both increase or both decrease)

negative association

two variables move in opposite directions

variance

a numerical measure of how spread out a set of data points is around their average (mean)

coefficient of variation (CV)

the standard deviation (SD) expressed as a percentage (%) of the mean

SD/mean * 100

how to find median in a data set

quartiles

values that partition the data into quarters

interquartile range (IQR)

difference between the 3rd (Q3) and 1st (Q1) quartile of the data

• spans 50% of the data

how to find IQR in a data set

features of box and whiskers plot

• shows max/min, median, skewness, spread of data, quartiles, and interquartile range

cumulative relative frequency (%) or (N)

how many observations are less than or equal to a given value 

how to calculate cumulative relative frequency for a data set

1. Order data from smallest to largest

2. Start with first frequency; add frequencies and sum

how to calculate the proportion of observations in a given category for a data set?

the most important descriptive statistic for a categorical variable

# of observations in category/total # of observations

sampling distribution

describes how an estimate varies across repeated samples from the same population

• as # of observations increases, the spread (and uncertainty) decreases

• is less variable than the distribution of individual observations

standard error (SE)

measures the uncertainty of an estimate 

• reflects precision of estimate

• as sample size increases, the standard error of mean decreases

confidence interval

a range of values surrounding the sample estimate that is likely to contain the population parameter

captures the true mean in 95% of repeated samples

2SE rule

• a rough approximation of the 95% confidence interval for a mean can be calculated as the sample mean +/- 2 standard errors (SE)

error bars

lines on a graph extending outward from the sample estimate to show uncertainty about the value of the parameter being estimated

• displays uncertainty, not spread of data