Crystallography & Diffraction-Exam 1

What is symmetry?

Invariance to a type of types of transformation

What are 4 types of transformation we can apply?

1. reflection

2. rotation

3. translation

4. scaling/fractal

Any combination of the above

Reflection Transformations

Operates by mirroring the object about a defined mirror plane in 3D (line in 2D, point in 1D)

Rotational Transformations

Is relative to a fixed point or axis in space. “N-fold” elements, rotated 360 degree/n through the axis

Translational transformations

A point continuously repeats after a spatial translation

What is a lattice

A periodic array of points that fills a space, where the environment of each point is identical.

What do lattices represent in periodic (crystalline) structures?

The translational symmetry.

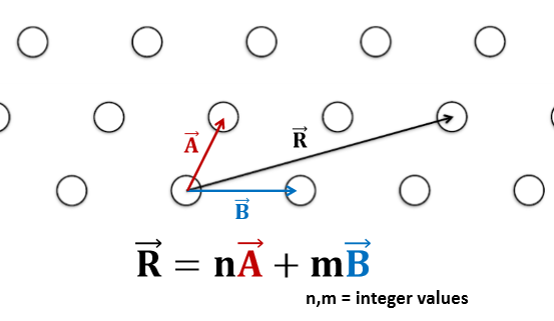
Define a lattice vector mathematically

R = nA + mB (n, m = integer values; bold lettering = vector)

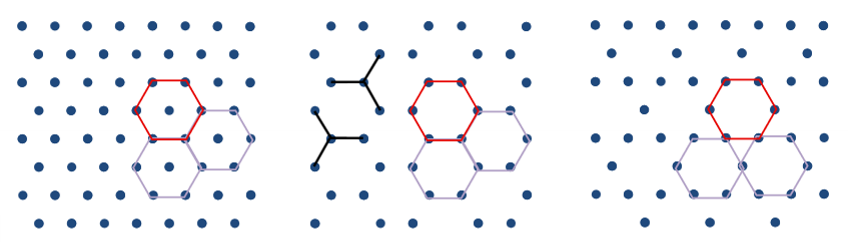
Which of these hexagons constitute a lattice?

1. Yes: Fills space & lattice points (corners) have identical environments

2. No: Fills space but does not have identical environments at the lattice points (corners)

3. No: Does not fill space or have identical environments at the lattice points (corners)

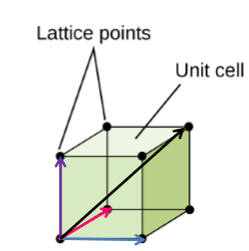
Unit cell

Encloses a repeating unit (an area in 2D, volume in 3D) of the lattice. More than one can be constructed

Primitive unit cell

Encloses the smallest area/volume of space possible, containing only one lattice point (generally at the corners)

Lattice Basis (motif)

Lattice provides a scaffold and what is inside the unit cell is the basis or motif

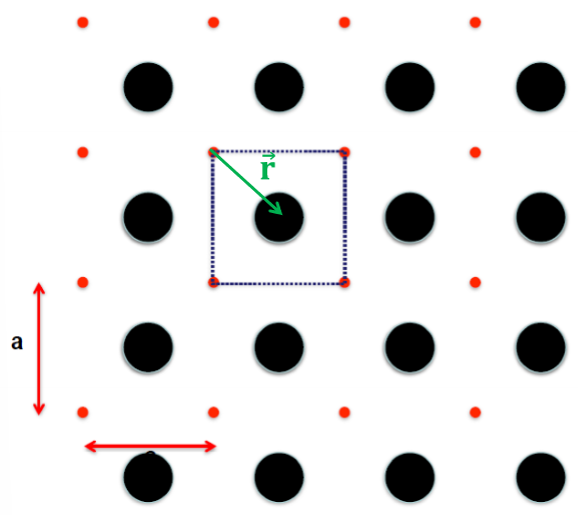
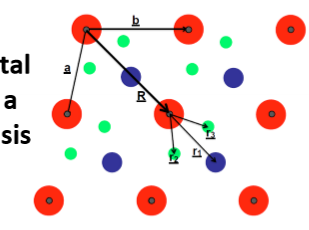
Basis vector r

The atom’s position relative to the lattice can be described by the basis vector r

Everything located within a primitive unit cell forms a valid basis.
True/False?

True

Does the variant need to be located on the corners of the lattice to be considered a lattice + basis?

No - neither variant needs to follow this requirement.

What is a crystal structure?

A lattice decorated by a basis

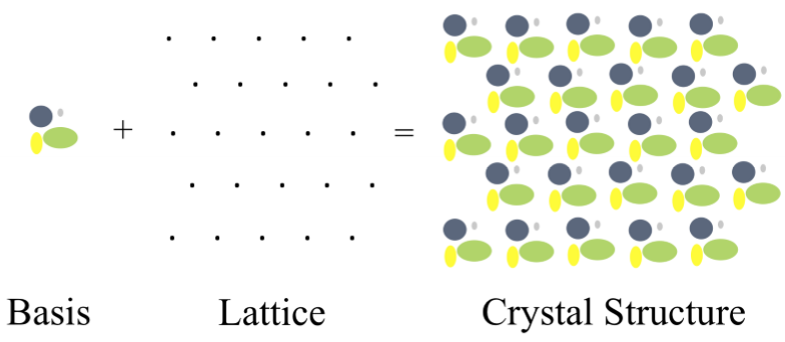
What are the symmetry effects of the basis?

Adding a basis can reduce the symmetry of a crystal, the lattice only sets the symmetry elements possible, some can be removed.

How can you represent a crystal mathematicaly?

A lattice vector plus a basis vector addition

Isometric transformations

Transformations that preserve the distance between points in Cartesian coordinate systems. Excludes scaling symmetry

What are 3 1D symmetry elements?

• 1D translation

• 1D reflection

• 1D reflection + translation

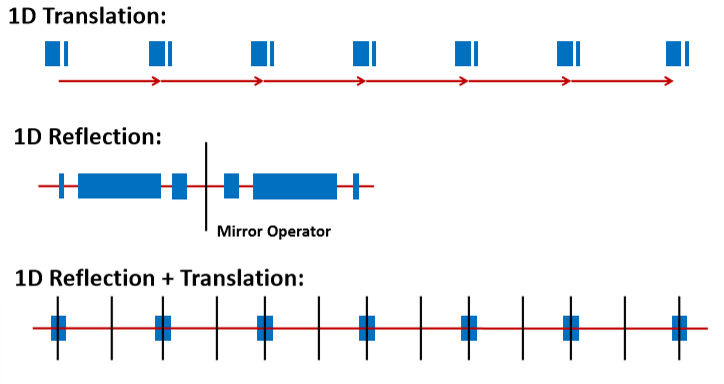
Why is there no 1D rotation?

In 1D the only rotation available is the equivalent of a reflection

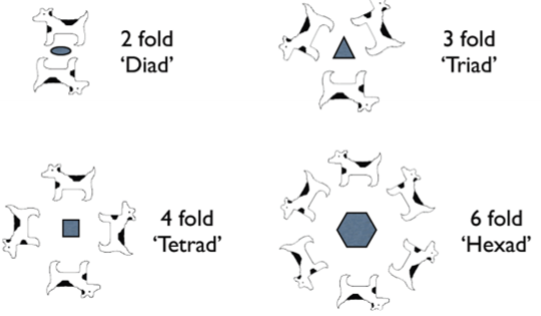
2D rotation symmetry symbol

Denoted by a polygon of matching symmetry at that point

Transflection (Glide) Symmetry

Involves simultaneous mirroring and a fixed fractional lattice translation of an object about a glide line (or glide plane in 3D) in a single action.

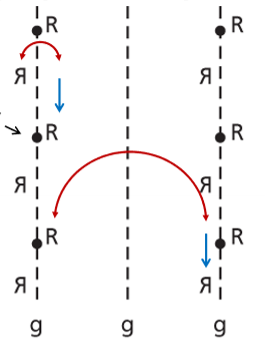
Why can’t glide occur at 1/3 of the spacing?

Odd numbers only repeat at twice the spacing, breaking the lattice condition.

Why is there no rhombohedral (a = b, gamma =/= 60 degrees, 90 degrees) lattice?

Rhombohedral is just a special case of the rectangular c-lattice and shares the same symmetry.

What are the 5 unique lattices in 2D?

1. Oblique P

2. Rectangular P

3. Rectangular C

4. Square P

5. Hexagonal P

What are 2D point groups?

10 ways that symmetry operators can be mutually arranged within a crystal about a single point in 2D space.

2D plane groups

By combining all possible combinations of the 2D plane lattices, with basis sets in the ten 2D point groups, 17 different plane groups can be constructed.

All patterns that repeat in 2D will follow one of these.

What are the steps for identifying symmetry in a 2D plane group?

1. Identify the points with the highest rotational symmetry

2. Identify a set of four of theses points that constitute a lattice and construct a unit cell

3. Identify any points with lower rotational symmetry within the unit cell

4. Identify any mirror planes in the cell

5. Identify the glide planes

Antisymmetry

Allowing for multiple colors or variations of geometrically similar objects. Also known at counterchange patterns in 2D.

What is a situation where antisymmetry is important in materials science?

Magnetic antisymmetry. The magnetic poles of atoms have a directional alignment.

Mathematical representation for a 3D lattice

R = lA + mB + nC + Basis

Inversion Symmetry

Occurs about a point called the center of symmetry. All features located at position (x, y, z) relative to the point also appear at position (-x, -y, -z)

What is the same operator as a 3D inversion in 2D?

A diad in 2D

Inversion Axes (Rotoinversion)

Compound symmetry elements, involving rotation about an axis followed by a point inversion (typically applied at the halfway point of the axis through the cell)

How are inversion axes labeled?

Denoted with an overhead bar.

What does this mean: 4/m

An axis over m denotes a mirror plane is located perpendicular to it.

Screw Axes (rotary translation)

Combine a translation step with rotation

How are screw axes denoted?

N_m where N is the rotation symmetry, and the translation is by m/N applied N times.

How are 4₁ and 4₃ different from each other?

They have different chirality. 4₁ has left-handed chirality and 4₃ has right-handed chirality.

Do the 6₂ and 6₄ axes have a handedness?

Yes, they are chiral. 6₂ is right-handed and 6₄ is left-handed. Both screw axes form a double helix.

3D Glide Notation

Denoted by whether it follows an axis (a, b, c), a diagonal (n), or in some cases if it moves by ¼ increments rather than half the cell (d, for diamond).

Steps for finding an equivalent position?

1. Find the position relative to the symmetry operator (x, y, z) - (x_s, y_s, z_s)

2. Find the symmetric positions in coordinates relative to the operator (x_r, y_r, z_r)

3. Add the relative positions to the location of the operator (x_r, y_r, z_r) + (x_s, y_s, z_s)

Symbols for reflection or glide planes?

Brackets in the corner, arrows denote glide direction

Space group notation

Hermann-Mauguin (aka International Symbol). Starts with the crystal type (P, I, C, F) followed b symmetry operations.

0th rank tensor

scalar, relates 2 scalars

1st rank tensor

vector, relates a scalar and vector

2nd rank tensor

Matrix, relates 2 vectors or a matrix and a scalar

3rd rank tensor

relates a vector and a matrix

4th rank tensor

relates two 2nd rank matrices

Crystal Directions Labeling

3 component vector using whole integers u, v, w of the a, b, c lattice translations. Direction noted [uvw].

unit vectors

Divide the vector by its scalar magnitude.

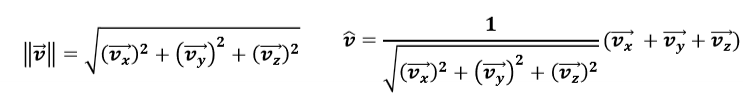
Miller indices

Standard naming convention for planes within a crystal

Crystal Planes Labeling

Pick an origin/corner the plane isn’t on. Measure intercepts on 3 primary axes Take reciprocal of each intercept. Reduce until the smallest integer set. Result is plane (hkl)

Lattice Plane repetitions

Series of planes that all share the same miller indices and are completely identical in both spacing and orientation.

Because of periodicity, every plane crosses a lattice point, meaning there is always a plane located at 0, 0, 0.

Plane families

Denoted {hkl}

a group of symmetrically equivalent planes.

Miller-Bravais Indices

Used for haxagonal crystals and are nearly identical to miller indices only a fourth axis (a₃) is added.

(hkil) where i = -(h + k)

What is the normal vector for cubic crystals?

[hkl] because (a=b=c)

Zone Axis

All planes with intersections along the same crystal direction are parallel to each other to form a zone axis

How would you figure out if a plane is in a zone?

Weiss Zone Law

Weiss Zone Law

If a direction lies in the plane, it must be 90 degrees to the plane normal. If a plane is in a zone, the dot product is zero.

How would you figure out what zone axis is shared by two planes?

The common zone will be at 90 degrees to each of the plane normals. The cross-product of the two plane normals is therefore the zone axis.

What is the planar space d_hkl for an arbitrary series of planes be dependent upon?

The crystal system

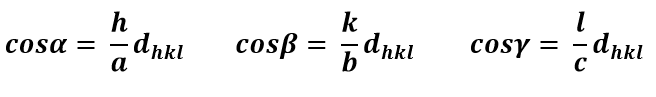
What is the equation for the interplanar spacing of cubic/tetragonal/orthorhombic?

1/d_hkl = h²/a² + k²/b² + l²/c²

Crystallographic Pole

Normal vectors are projected from each plane to a sphere of constant radius

Stereographic projection

Conformal so while the scaling changes across the projection, in a local region, the angles and distances are approximately correct.

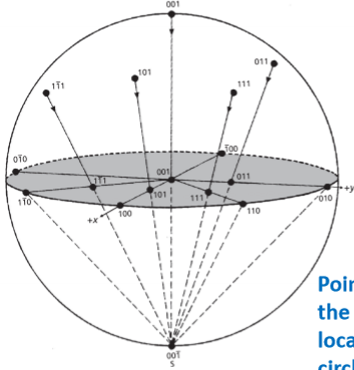
Stereographic net

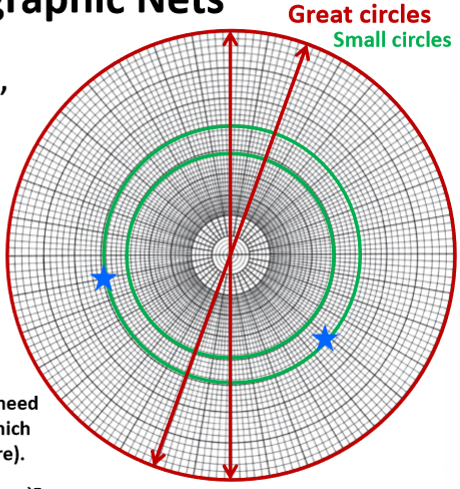
Stereographic grid patterns.

Longitude - all great circles (pass through center)

Latitude - all small circles except for the equator (equatorial plane)

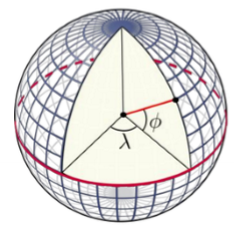
Polar Net

Project a grid from on top of a globe

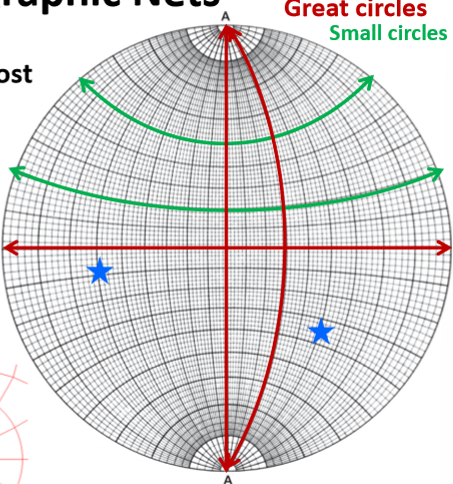
Wulff net

Version of a pole net with a 90 degree rotated z-axis.

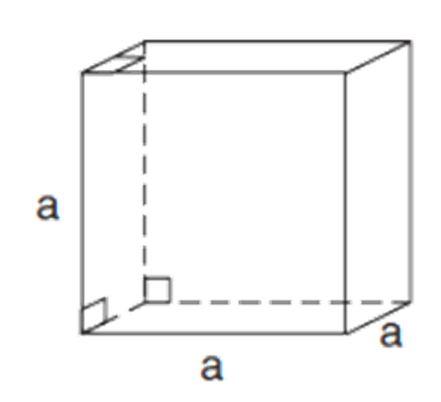
Which Bravais lattice is this?

Cubic

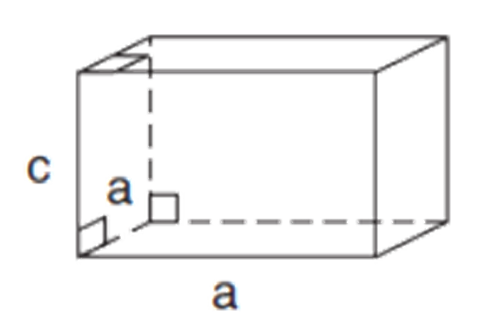
Which Bravais lattice is this?

Tetragonal

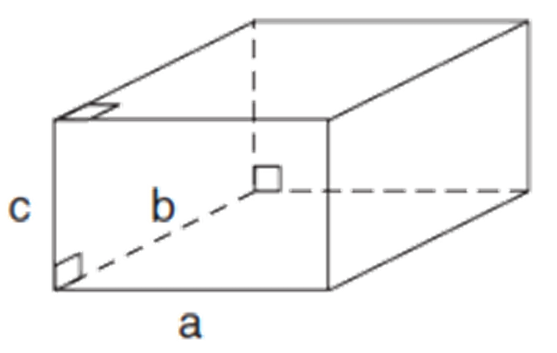
Which Bravais lattice is this?

Orthorhombic

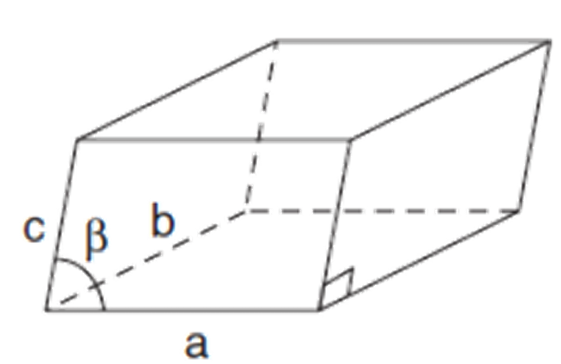
Which Bravais lattice is this?

Monoclinic

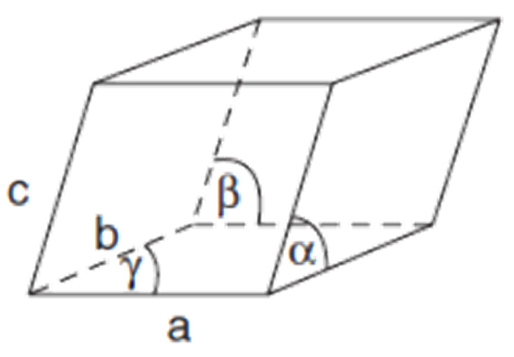
Which Bravais lattice is this?

Triclinic

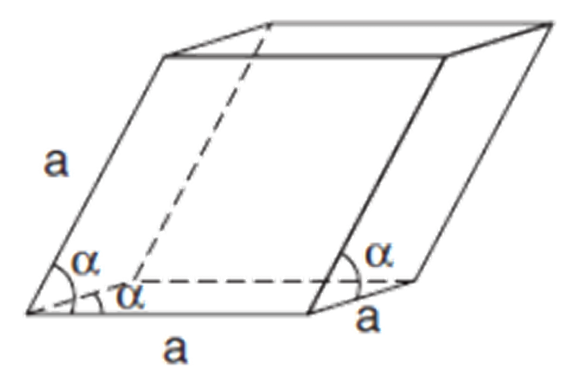
Which Bravais lattice is this?

Trigonal

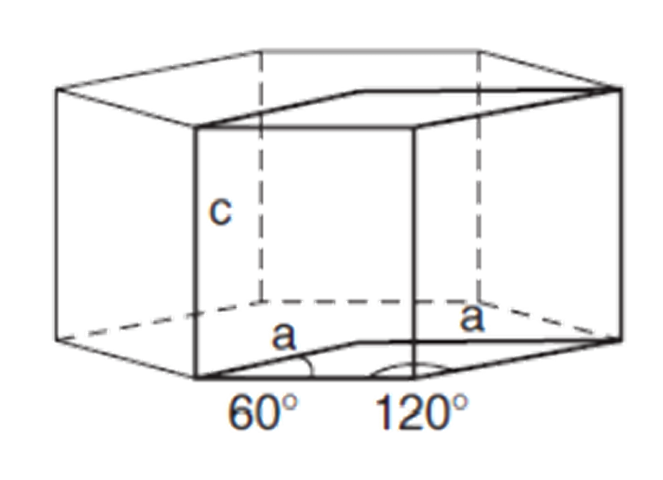
Which Bravais lattice is this?

Hexagonal

What is are the minimum symmetry elements contained in a triclinic system?

no rotation symmetry

What is are the minimum symmetry elements contained in a monoclinic system?

One 2-fold rotation (or rotation-inversion) axis

What is are the minimum symmetry elements contained in a orthorhombic system?

3 perpendicular 2-fold rotation (or rotation-inversion) axes

What is are the minimum symmetry elements contained in a Trigonal system?

One 3-fold rotation (or rotation-inversion) axis

What is are the minimum symmetry elements contained in a hexagonal system?

One 6-fold rotation (or rotation-inversion) axis

What is are the minimum symmetry elements contained in a tetragonal system?

One 4-fold rotation (or rotation-inversion) axes

What is are the minimum symmetry elements contained in a cubic system?

Four three-fold rotation (or rotation-inversion axes)

Hasse Diagram

Way to show graphically which symmetries are sub-sets of others