Fluid Mechanics Exam II Concepts

Conceptual questions for Fluid Mechanics Exam II covering Chapters 4-6 of "Fundamentals of Fluid Mechanics." Material from lecture slides and Midterm review.

Streamline

Instantaneous line tangent to velocity vectors (no flow across it)

Streakline

Traces the path of fluid particles released from a fixed point in the past

Pathline

Actual trajectory of a single fluid particle over time

What is the material derivative (D/DT) in its expanded form?

Tells us that the total rate of change of a fluid property where:

(∂/∂t) is Local Change ( Time Dependent, 0 for steady state)

(V⋅∇V) is Convective change due to fluid motion

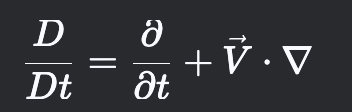
What is the continuity equation for incompressible flow in differential form?

Means no net mass accumulation in a fluid element

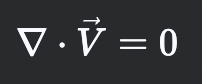
What is Reynolds Transport Theorem (RTT)?

Connects system and control volume perspectives where the right side represents 1. the time rate of change of B inside the control volume and 2. the net flux of B across the control surface due to flow

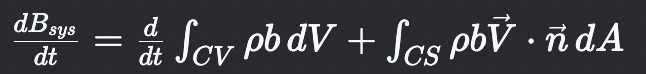
What is the mass conservation equation for a steady flow control volume?

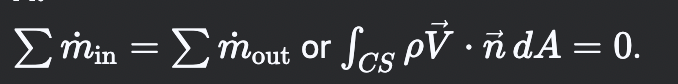
What assumptions simplify the Bernoulli equation?

Steady flow → d/dt=0

Incompressible → ρ=const.

Inviscid → μ=0

Along the streamline

What is head loss in the energy equation?

h_L is the energy loss due to friction (viscosity μ), Negligable when μ=0

What are the Navier-Stokes equations? (Unsimplified)

Newtons 2nd law for fluids, Balances inertia with pressure, viscous, and body forces

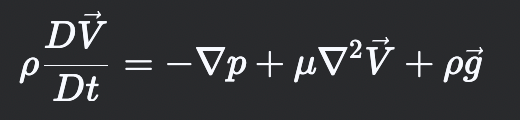
What is the Naview-Stokes equation? (Simplified)

Essentially Euler’s equation

What is the stream function (ψ)?

Lines of constant ψ are streamlines (No flow accross), used for 2D incompressible flow to satisfy continuity.

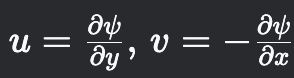
How does viscosity affect the velocity profile in a pipe?

Viscosity creates a parabolic profile due to shear stress

What is the difference between a streamline and a pathline?

A streamline is an instantaneous line tangent to velocity vectors; a pathline is the actual path a fluid particle follows over time

If fluid flow is steady, do streamlines and pathlines coincide?

Yes, in steady flow streamlines, pathlines, and streaklines are identical

What does incompressible flow imply about the divergence of velocity (∇⋅V)?

(∇⋅V)=0 Volume of a fluid element doesn’t change over time

When is Reynolds transport theorem (RTT) used?

When we need to relate system properties to control volume properties. Lagrangian view → Eulerian view

Why can’t Bernoulli’s equation be applied through a pump or turbine?

Because it doesn’t account for work/energy, instead use energy equation.