pre cal midterm review

hyperbola definition

a set of all points in a plane such that the absolute value of the difference from F1 and F2 is equal

parabola definition

set of all points are equidistance from a focus to a directrix

ellipse definition

set of all points where sum of each of the distances from focal points is d

circle definition

all points in a plane that are fixed distance from a fixed point

equation of a circle

(x-h)²+(y-k)²=r²

horizantal hyperbola equation

(x-h)²/a² - (y-k)²/b² =1

verticl hyperbola equation

(y-k)²/a² - (h-k)²/b² =1

horizantl parabola equaiton

(y-k)²=4p(x-h)

vertical parabola equation

(x-h)²=4p(y-k)

horizantal ellipse equaiton

(x-h)²/a² + (y-k)²/b²=1

verical ellipse eqution

(x-h)²/b² + (y-k)²/a²=1

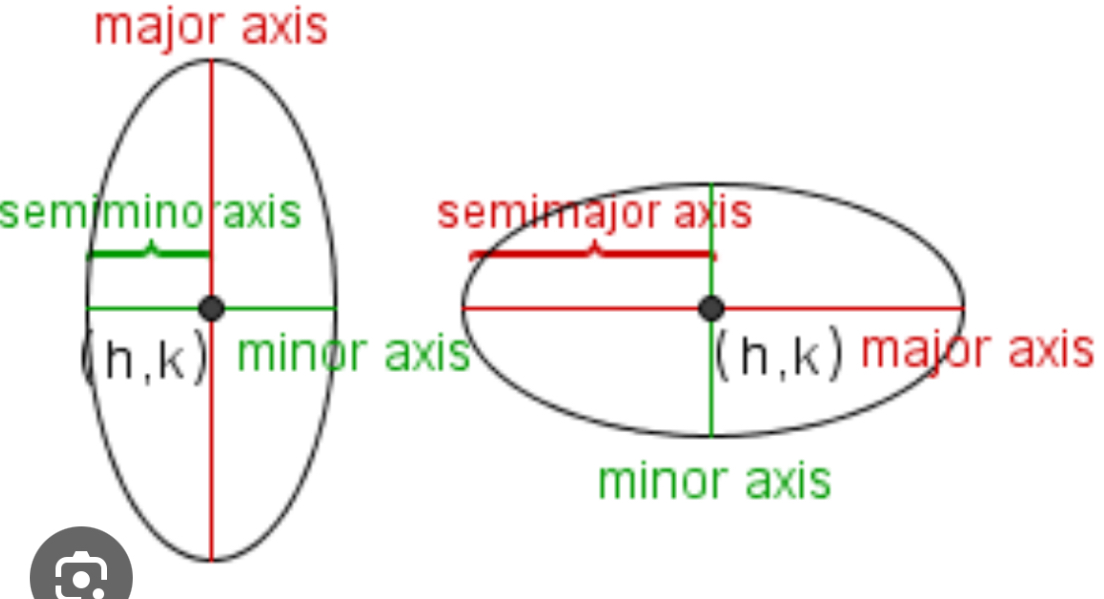
which one is a vertical ellipse?

on the left

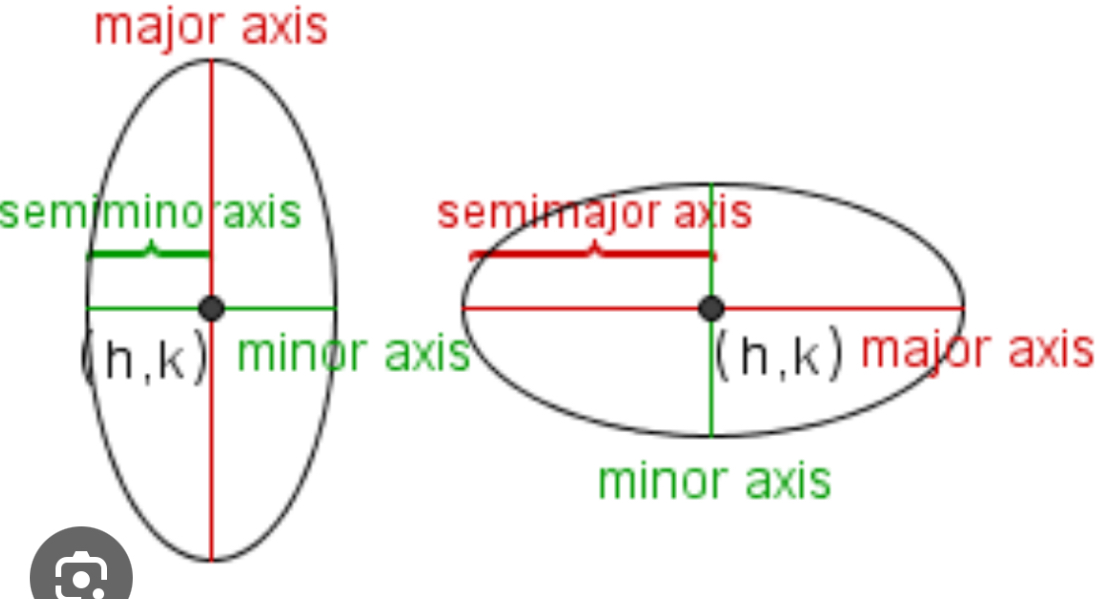
which one is a horizontal ellipse?

one on the right

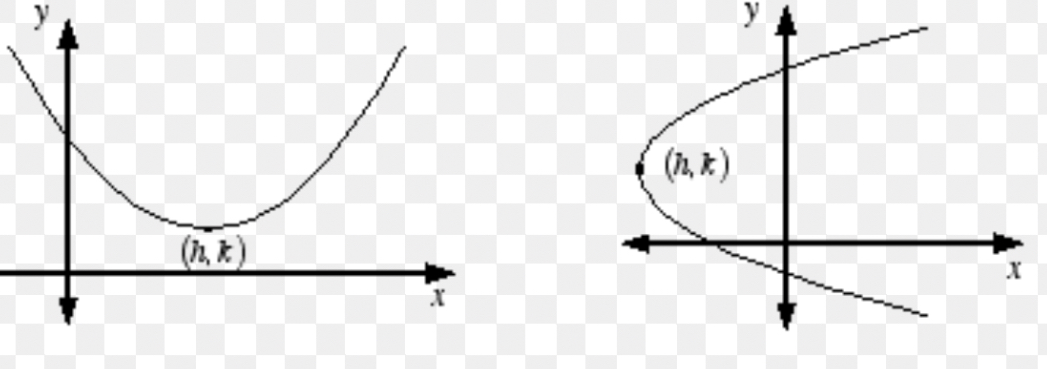
which one is a vertical parabola

one on the left

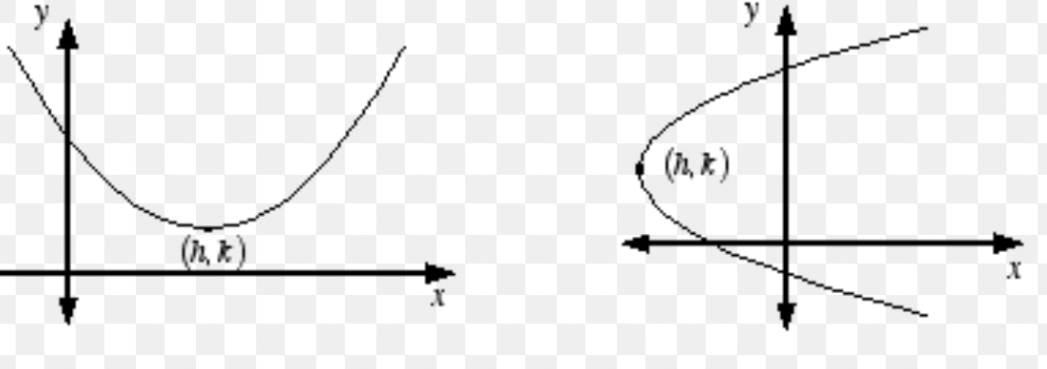
which one is a horizontal parabola

one on the right

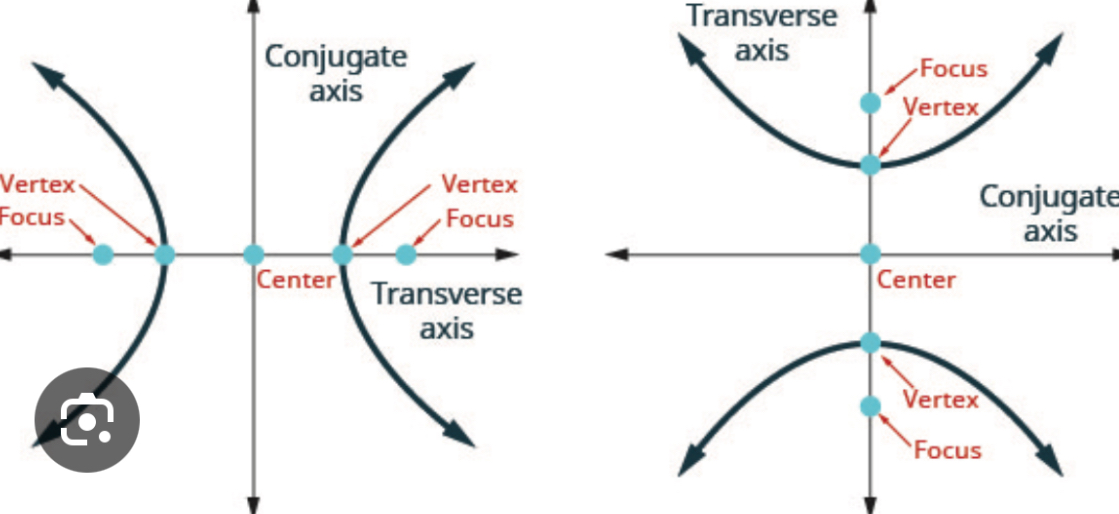
which one is a vertical hyperbola

one on the right

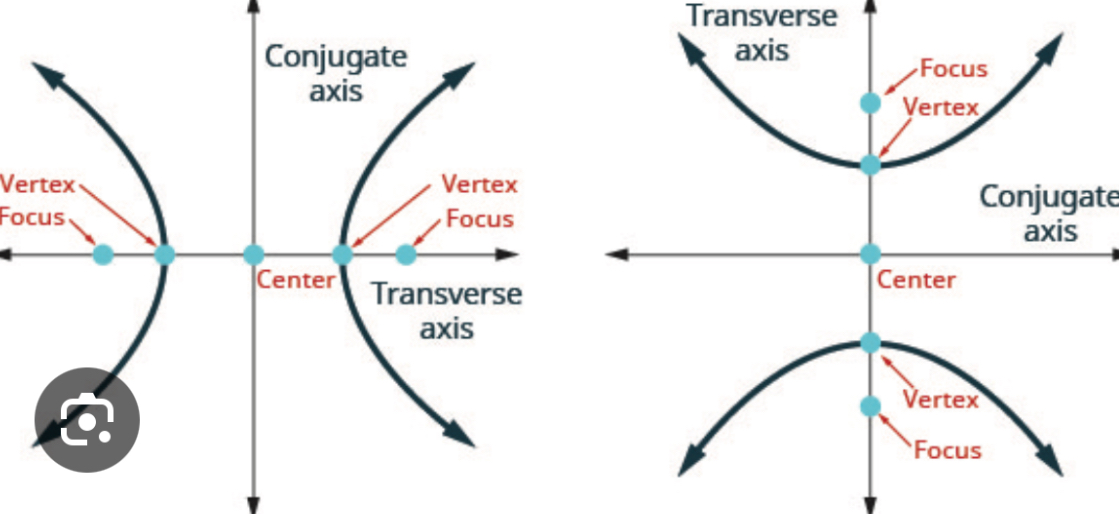
which one is a horizontal hyperbola

one on the left

what is the lacey’s rectum equal to?

4p and the focal diameter

what is p

the distance from the vertex to the focus

what is the directrix equation

x or y = h or k -p

what is the focus point for a horizontal parabola

(h+p,k)

what is the focus point for a vertical parabola

(h, k+p)

is 4p= a negative number

the parabola is facing downwards(vertical) or to the left(horizontal)

what are the vertices of a horizontal hyperbola

(h+-a,k)

what are the vertices of a vertical hyperbola

(h,k+-a)

what is c

the distance from the central to a focus point

what is the foci of a vertical hyperbola

(h,k+-c)

what are hr dock of a horizontal hyperbola

(h+-c,k)

what is eccentricity equal to

c/a

what is the ep major of a horizontal ellipse parallel to

the x axis

what is the ep minor of a horizontal ellipse parallel to

the y axis

what is the ep major of a vertical ellipse parallel to

the y axis

what is the ep minor of a vertical ellipse parallel to

the x axis

what is c²=a² - b² used for

ellipses

what is c²=a²+b² used for

hyperbolas

locus definition of a circle

the locus of all points in a plane that are a fixed, constant distance from a central point

locus definition of an ellipse

the locus of points in a plane where the sum of the distances from any point on the curve to two fixed points (foci) is a constant

locus definition of a parabola

the locus of all points that are equidistant from a fixed point (the focus) and a fixed line (the directrix)

locus definition of a hyperbola

the locus of points where the absolute difference of the distances from two fixed points (foci) is a constant

log function form

y=log (x+b)

a

half life formula

N(t)=N (1/2) ^t/t1/2

o

general conics equation

𝐴𝑥2+𝐵𝑥𝑦+𝐶𝑦2+𝐷𝑥+𝐸𝑦+𝐹=0

bijective function

both surjective and injective (every y value is used and every y value correspond to a singualar x value)

injective/ one to one function

every y - value corresponds with a singular x value, ex.lisd students to their chromebooks (everyone has there own but just 1)

surjective

every y value is used, even if an x value leads to 2 y values, ex. at a resturaunt 3 friends order different things but two friends order the same thing

domain for polynomial funtions

all real numbers

domain for rational function (fraction)

excludes factors that make the denominator 0

domain for square root function

excludes factor the make the number under the square root negative

domain for composite functions

find each components' domain restrictions and find the intersecction

why would a graph not have an inverse function?

the y values might repeat (in the original function) so in the inverse function it would make the x values repeat, making it not a function

sum-sum funcitons

linear

sum - constant 2nd difference functions

quadratic

product - product functions

power

sum -product funcctions

expoential

product - sum functions

logarithmic

on a graph a filled in dot means

greater/less than or equal to

on a graph an open dot means

greater/less than

if a value is greater than 1 and is in parenthesis/absolute value bars/under the root with x the graph has a

horizantal compression of the value touching x

if a value is less than 1 and is in parenthesis/absolute value bars/under the root with x the graph has a

horizantal stretch of the reciprocal of the value

if a value is greater than 1 and is in front of the parenthesis/absolute value bars/ root with x the graph has a

vertical stretch of the value

if a value is less than 1 and is in front of the parenthesis/absolute value bars/root with x the graph has a

verticl compression of the value

log(M) + log(N) also =

log(MN)

log(M) - log(N) also =

log(M/N)

log(M)^N also =

Nlog(M)

when something is raised to a fraction

power/root (raise to power of numerator then take the root of the denominator)

e =

2.7

exponential growth rate

A(t)=P(1+r)^t

compound growth rate

A(t)=P(1+r/n)^nt

compounded continuously

A(t)=Pe^rt

in the equation y=a•b^kt if b is greater than 1

it’s a growth model

in the equation y=a•b^kt if b is between 0 and 1

it’s a decay model

if your given a growth/decay model with a numerator above the a•b^kt that number is

the carrying capacity of the model

log N = x can also be written as

a

a^x=N