MCAT Physics & Math [Ch. 1 Kinematics and Dynamics]

SI units:

Length

Mass

Time

Current

Amount

Temp

Luminous Intensity

Length:........................meter (m)

Mass (not weight): ........kilogram (kg)

Time: ..........................second (s)

Current: ......................ampere (A)

Amount of a substance: mole (mol)

Temperature: ...............kelvin (K)

Luminous Intensity:.......candela (cd)

in SI:

what is the derived unit for force (N)

what is the derived unit for Work and Energy (J)

what is the derived unit for power (Watt)

Newton [kg*m/s^2]

Joule [kg*m^2/s^2]

Watt [ kg*m^2/s^3]

Vectors

are physical quantities that have both magnitude and direction.

can be represented by arrows. the direction of the arrow indicated the direction of the vector. the length of the arrow is usually proportional to the magnitude of the vector quantity.

Vector quantities include:

displacement

velocity

acceleration

force

others.

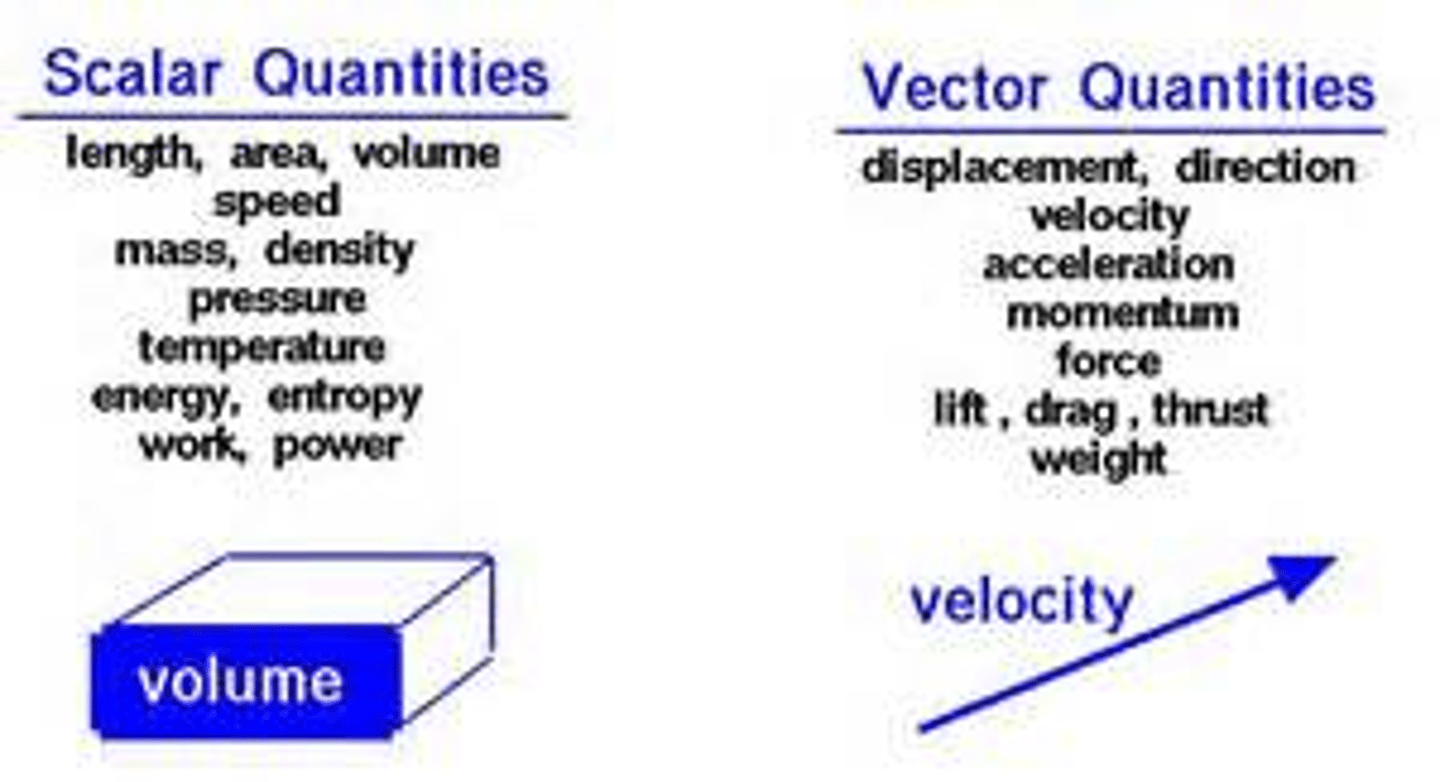
Scalars

are quantities that have magnitude only and no direction.

Scalar quantities include

distance, speed, energy, pressure, mass

resultant of vectors

the sum or difference of two or more vectors

tip-to-tail method

a way to find the sum or resultant of two vectors A and B, is to place the tail of B at the tip of A without changing either length or direction of either arrow.

The vector A+B is the vector joining the tail of A to the top of B.

Components of vectors?

each vector V has an x- and y-component where the V is the hypotenuse

Vector addition may be accomplished using:

1. tip-to-tail method

2. or by breaking a vector into its components and using the pythagorean theorem

The X-component is given by:

X = Vcosθ

the y-component is given by:

Y = Vsinθ

the direction (θ) of the resultant is given by:

θ = tan ^-1 (Y/X)

Vetor subtraction is accomplished by:

changing the direction of the subtracted vector and then following the the procedures for vector addition.

A-B = A + (-B)

Multiplying a vector by a scalar:

changes the magnitude of the vector and may reverse the direction.

B = nA

To find magnitude of the new vector B, you multiply A by |n|

to determine the direction of the new vector B, we must look at the sign on n. If n is positive, then B and A are in the same direction. if n is negative, then B and A are in opposite directions,

Multiplying vectors by vectors (Dot product)

Dot product

the dot product of two vectors A and B results in a scalar value. The dot product is the product of the vectors' magnitudes and the cosine of the angle between them.

A . B = |A| |B| cosθ

or

A = (a1, a2) B= (b1, b2)

A . B = a1b1 +a2b2

used when needed to generate a scalar quantity such as work

Multiplying vectors to get another vector (Cross product):

Cross Product

the cross product results in a vector quantity . The cross product is the product of the vectors' magnitudes and the sine of the angle between them.

A x B = |A||B|sinθ

used when generating a third vector like torque.

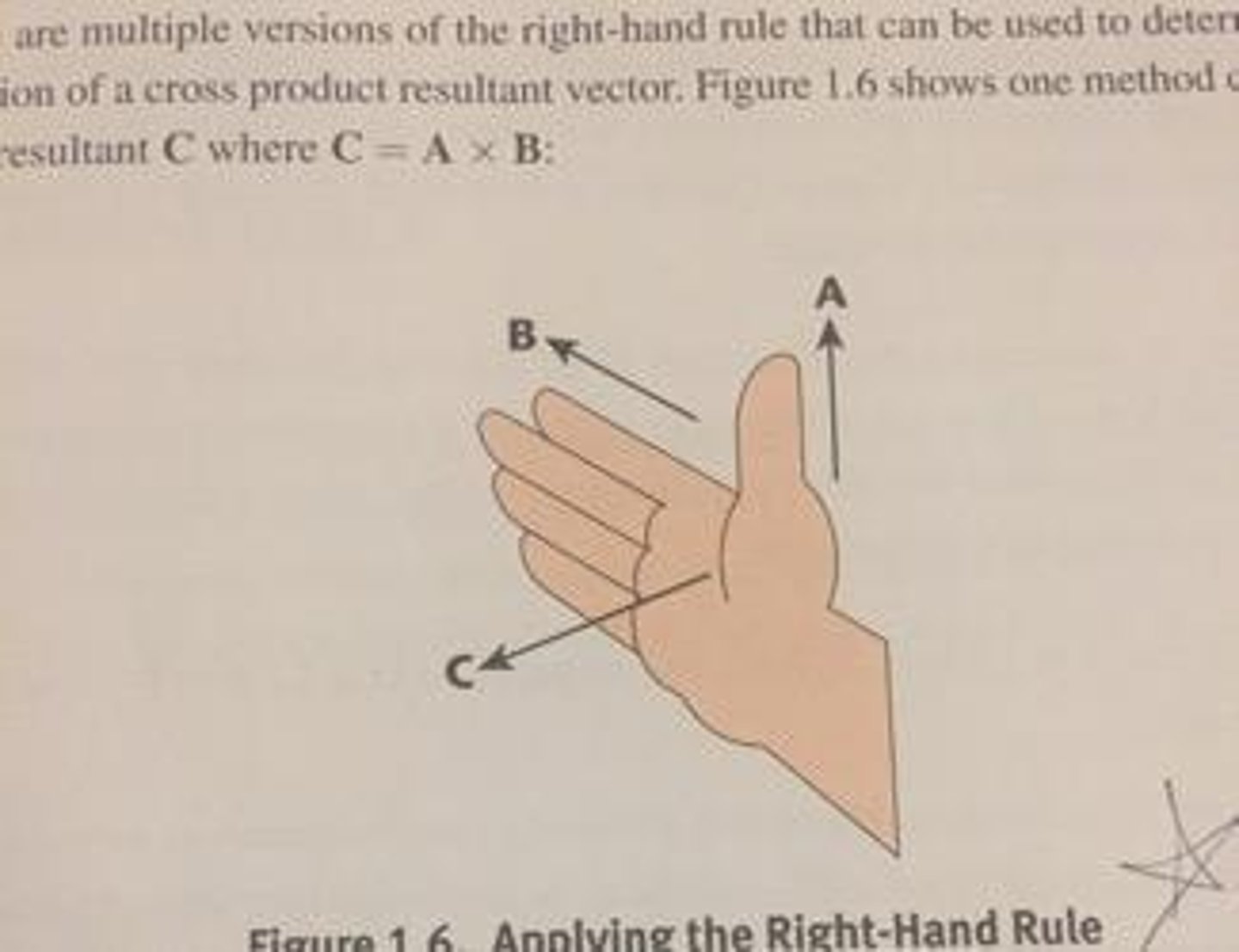
Right-Hand rule is used to?

used to determine the resultant vector's direction after two vectors have been crossed.

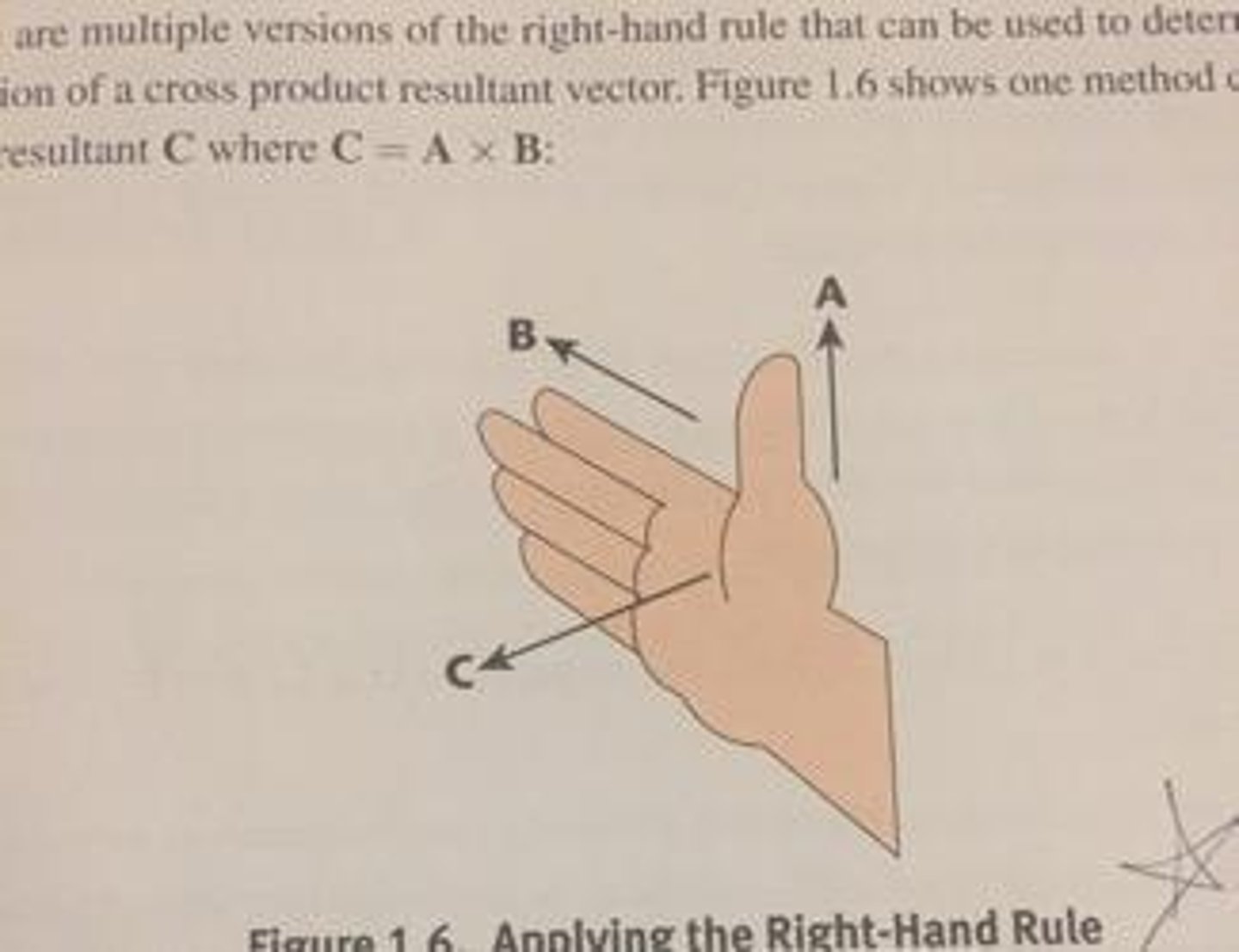
right-hand rule steps:

C = A x B

1. start by pointing your thumb in the direction of vector A. (The vector that is written first)

2. Extend your fingers in the direction of vector B. you may need to rotate your write to get the correct configuration of thumb and fingers.

3. Your palm establishes the plane between the two vectors. The direction your palm points is the direction of the resultant C.

IF A IS FIRST, THEN A IS THE THUMB. IF B IS FIRST IN PROBLEM (EX: D=B x A), THEN B IS THE THUMB

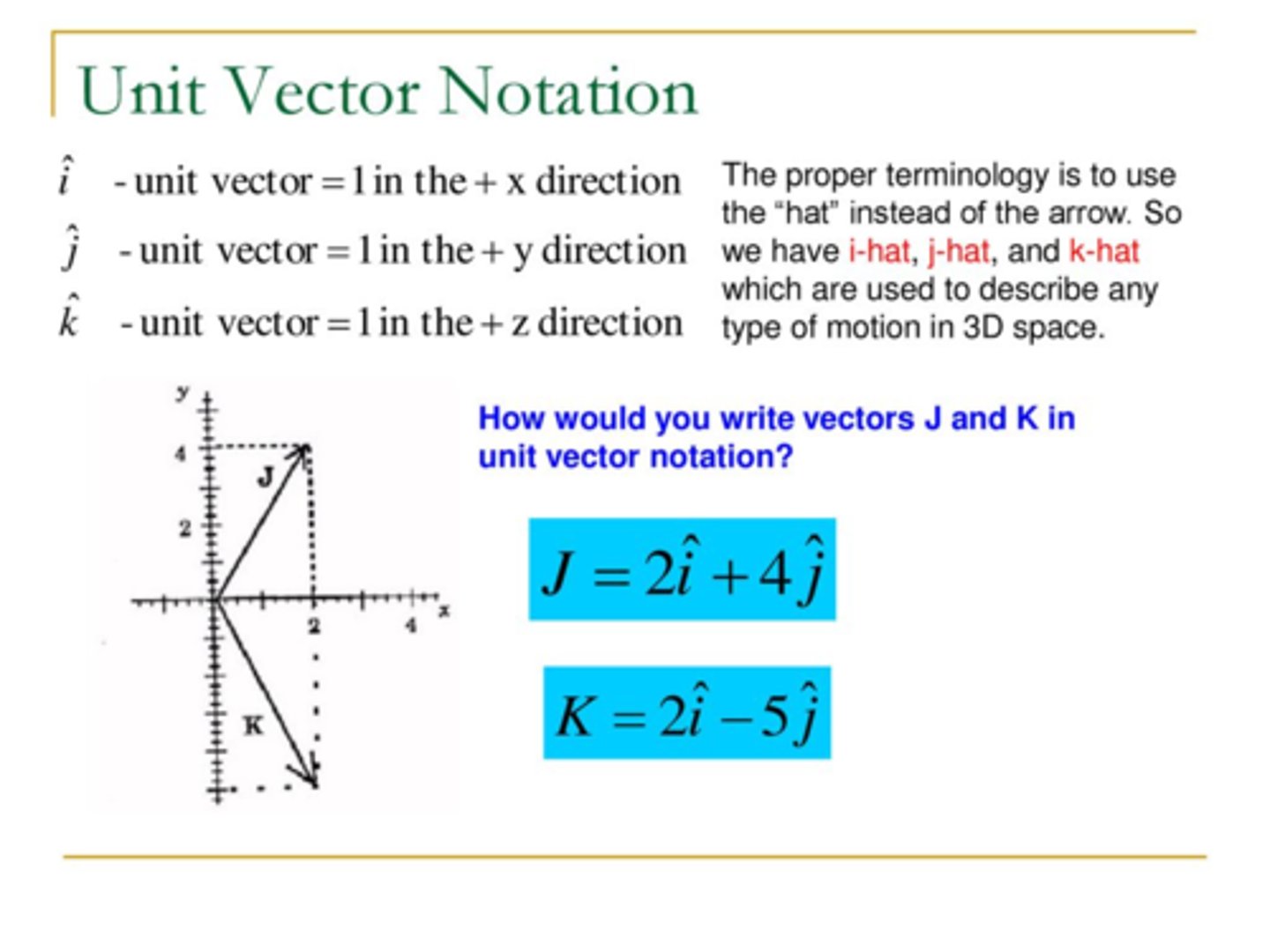
Unit vector notation

describes vectors by breaking them into there x, y and z components and are denoted by "i-hat", "j-hat" and "k-hat"

Scalar * scalar =

Vector * scalar =

Vector * scalar =

A scalar multiplied by a scalar will produce another scalar. For instance, distance divided by time is equal to speed, which is a scalar

A vector multiplied by a scalar is representative of the scalar product or the dot product and will always produce a vector.

Vector multiplied by a vector is representative of the vector product or the cross product and will produce a vector or scalar.

Displacement (x or d)

an object in motion may experience a chage in its position in space, known as displacement (x or d) this is a vector quantity and, as such, has both magnitude and direction.

Is the vector representation of a change in position. It is path independent and is equivalent to the straight line distance between the start and end locations

Distance (d)

Is a scalar quantity that reflects the path traveled.

scalar

Velocity (v)

is the vector representation of the change in displacement with respect to time.

vector

Speed (v)

is the rate of actual distance traveled in given unit of time.

scalar

Instantaneous Velocity (v)

is limit of the change in displacement over time as the change in time (Δt) approaches 0.

lim ( Δx/Δt )

Δt—> 0

Δx is the change in position

Δt is the change in time.

vector

Instantaneous Speed

is the magnitude of the instantaneous velocity.

scalar

Force (F)

The SI unit for force?

Is a vector quantity pf any push or pull that has the potential to result in an acceleration.

Newton which is equivalent to kg*m/s^2

Gravity

Is the attractive force between two objects as a result of their masses.

is an attractive force that is felt by all forms of matter.

Gravitational force between two objects:

Fg = (Gm1m2)/ r^2

G = universal gravitational constant

= 6.67x10^-11 Nm^2/kg^2

m1, m2 = masses of the two objects

r = distance between their centers of mass.

Friction

Is a force that opposes motion as a function of electrostatic interactions at the surface between two objects.

friction forces always oppose an object's motion and cause it to slow down or become stationary.

Static Friction (fs)

exists between two objects that are not in motion relative to each other.

exists between a stationary object and the surface upon which it rests.

However, static friction is only as large as necessary for the object to stay static and counteract the opposing force until the force due to static friction reaches its maximum amount.

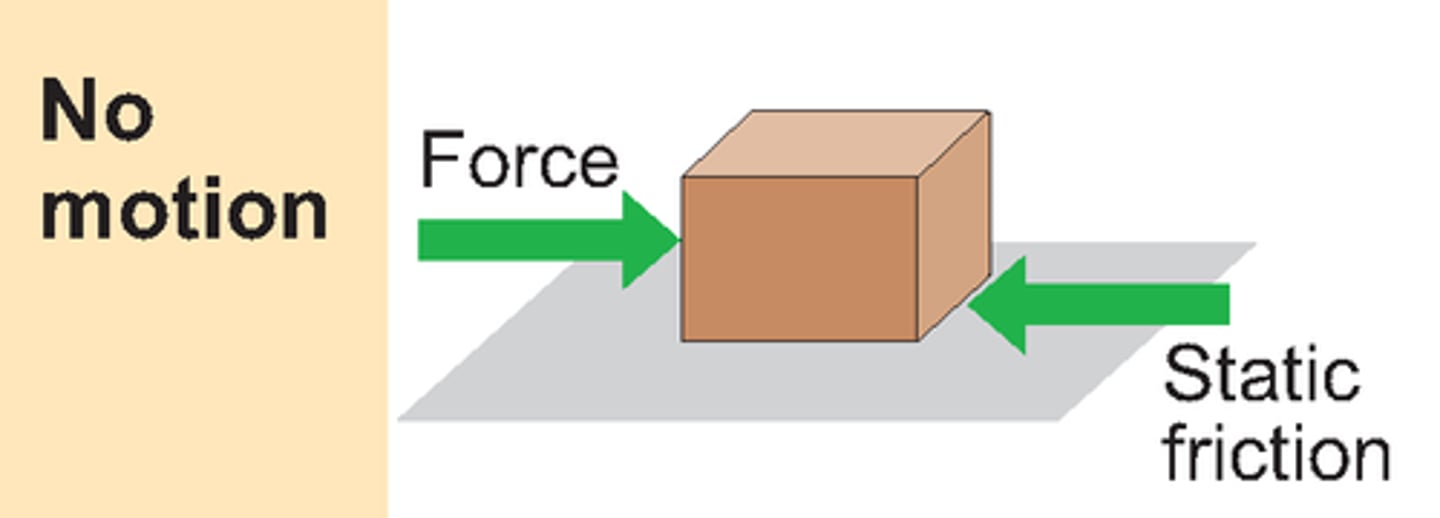
the equation that describes the magnitude of static friction:

0<= fs <= μsN

Where μs is the coefficient of static friction

N: is the magnitude of normal force.

coefficient of static friction μs

is a unitless quantity that is dependent on the two materials in contact. [always higher than the coefficient of kinetic friction]

Normal force

is the component of the force between two objects in contact that is perpendicular to the plane of contact between the object and the surface upon which it rests.

Kinetic friction (fk)

exists between two objects that are in motion relative to each other.

constant value

exists between a sliding object and the surface over which the object slides.

the equation that gives the magnitude of kinetic friction is:

fk = μkN

μk: coefficient of kinetic friction

N: is the normal force

this will only equal one constant value, where as the fs equation can be a range of values.

the coefficient of static friction will always be _______ compared to the coefficient of kinetic friction

be larger than the coefficient of kinetic friction.

It always requires more force to get an object to start sliding than it takes to keep an object sliding.

Coefficient of friction

depends on the two materials in contact.

The coefficient of static friction is always higher than the coefficient of kinetic friction.

Weight (Fg)

is a measure of gravitational force (usually that of the earth) on an object's mass.

vector

SI units for force N newtons

Acceleration (a)

is the vector representation of the change in velocity over time. Average or instantaneous acceleration may both be considered, similar to velocity.

is the rate of change of velocity that an object experiences as a result of some applied force,

SI Units: m/s^2

deceleration

acceleration in the direction opposite the initial velocity.

Instantaneous acceleration is defined as:

the average acceleration at Δt approaches zero.

a = lim Δv/Δt

......Δt—>0

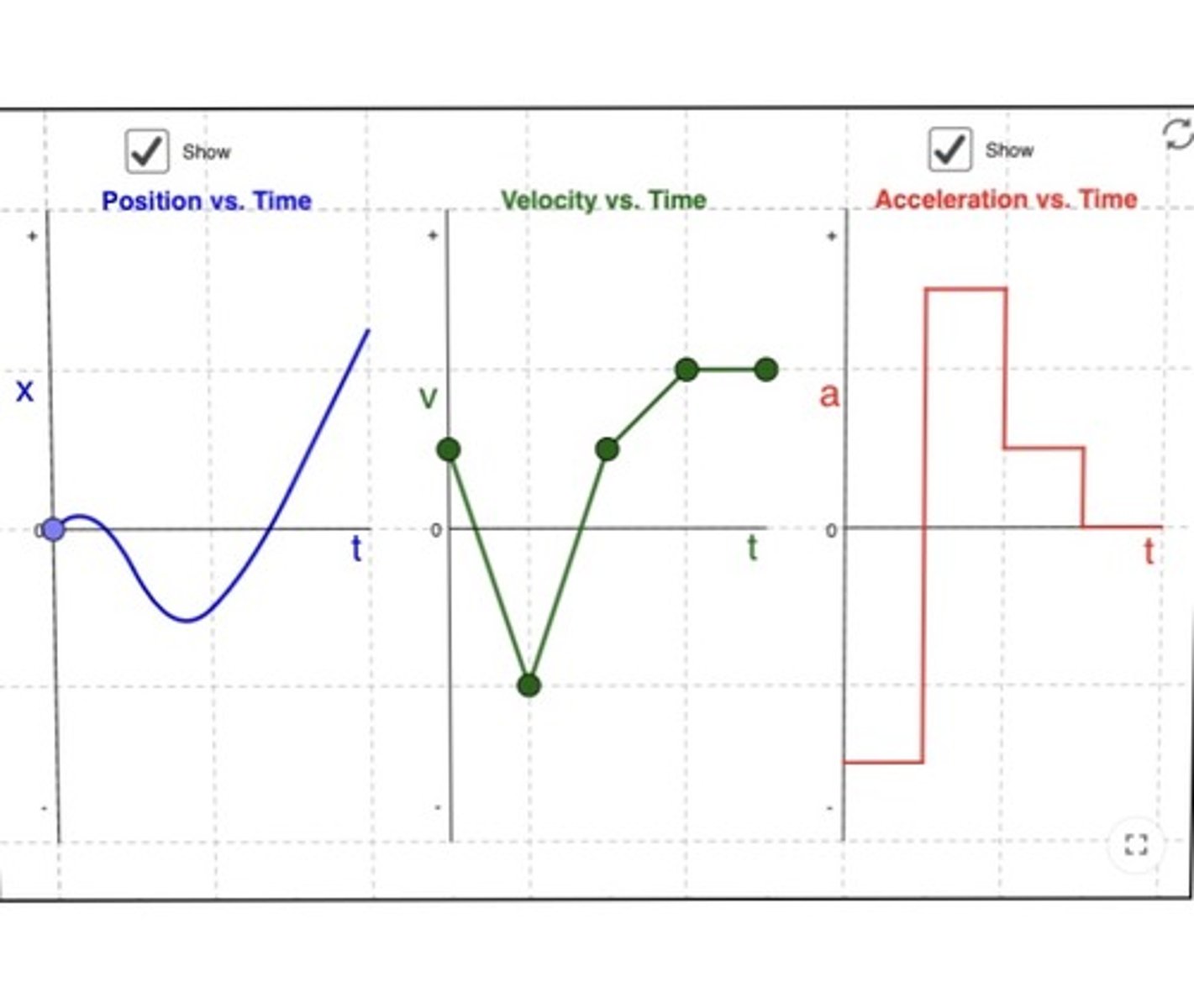
on the graph of velocity vs. time the tangent to the graph at any time t, which corresponds to the slop of the graph at that time, indicates:

The instantaneous acceleration

in other words, the derivative of the velocity function with respect to time is the instantaneous acceleration. because by definition the slope of the tangent line is the derivative.

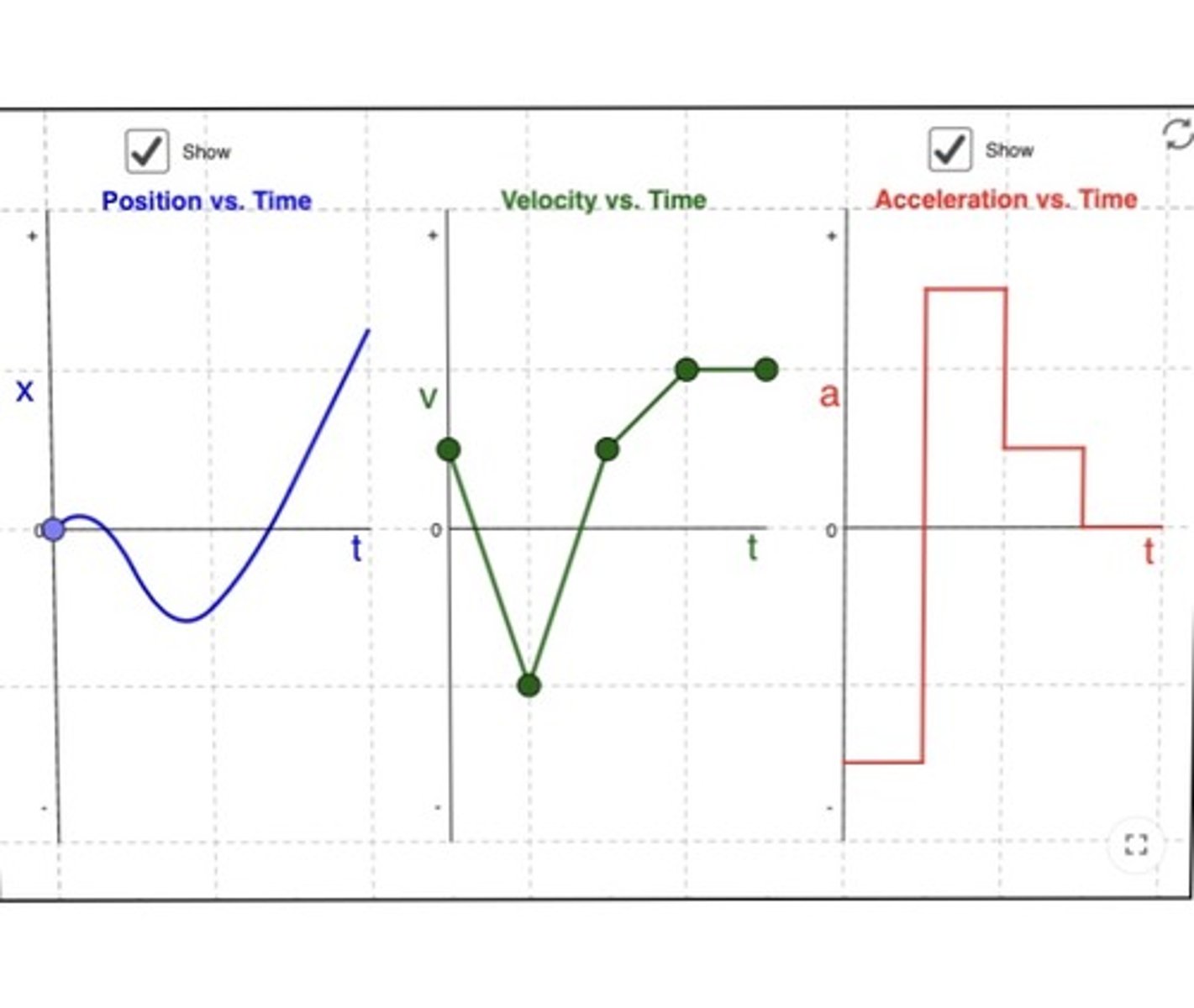
if slope is positive in a velocity-time graph,...

the acceleration is positive and is in the direction of the velocity

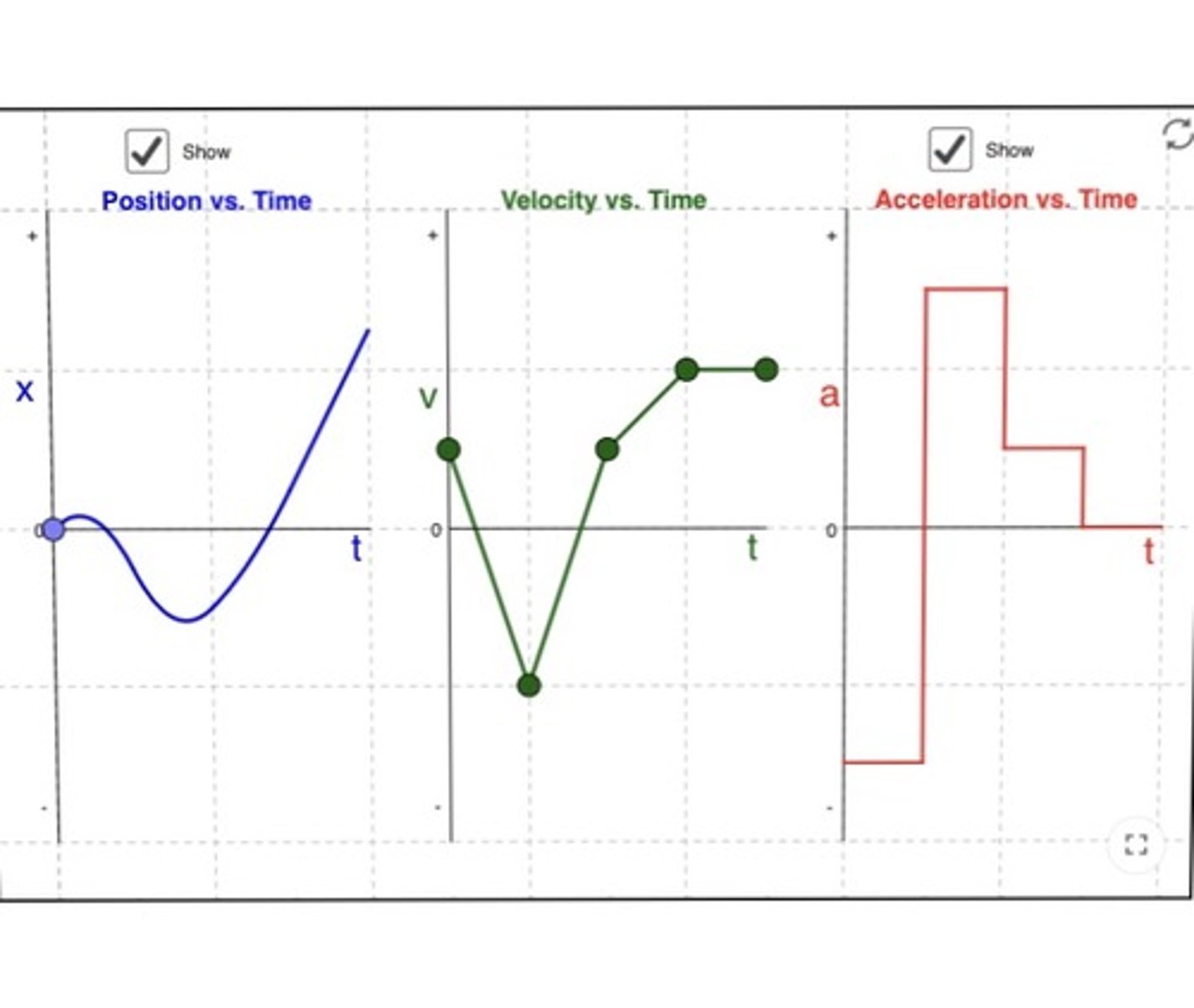
if slope is negative in a velocity-time graph,...

the acceleration is negative (deceleration) and is in the direction opposite of the velocity.

What is the equation that related mass and weight:

Fg = mg

Fg: weight of the object

m: mass of the object

g : acceleration due to gravity 10 m/s

Newton's first law (Law of inertia)

states that an object will remain at rest or move with a constant velocity if there is no net force on the object

[ Fnet = ma = 0]

Fnet : the net force

m: mass

a: acceleration

Newton's second law:

states that any acceleration is the result of the sum of the forces acting on the object and its mass

[ Fnet = ma ]

Fnet : net force

m: mass

a :acceleration

Newton's third law:

states that any two objects interacting with one another experience equal and opposite forces as a result of their interaction.

[FAB = -FBA ]

more formally, for every force exerted by object A on object B, there is an equal but opposite force exerted by object B on object A.

Linear motion

includes free fall and motion in which the velocity and acceleration vectors are parallel or antiparallel

the object's velocity and acceleration are along the line of motion, so the pathway of the moving object continues along a straight line.

example: a ball being dropped from some height. (free fall)

falling objects exhibit...

linear motion with constant acceleration.

common problem on MCAT

one-dimensional motion can be fully described by the following equations:

(1) v = vo +at

(2) x = vot + (at^2)/2

(3) v^2 = vo^2 + 2ax

(4) x = v~t

x : displacement vector

v : velocity vector

a : acceleration vector

v~ : average velocity

vo : initial velocity

t : time

Projectile motion

is a motion that follows a path along two dimensions. (the velocities and accelerations in the two directions [usually horizontal and vertical] are independent of each other and must, accordingly, be analyzed separately. Contains both an x- and y-component. Assuming negligible air resistance, the only force acting on the object is gravity. On the MCAT you will be able to assume that the horizontal velocity vx will be constant.

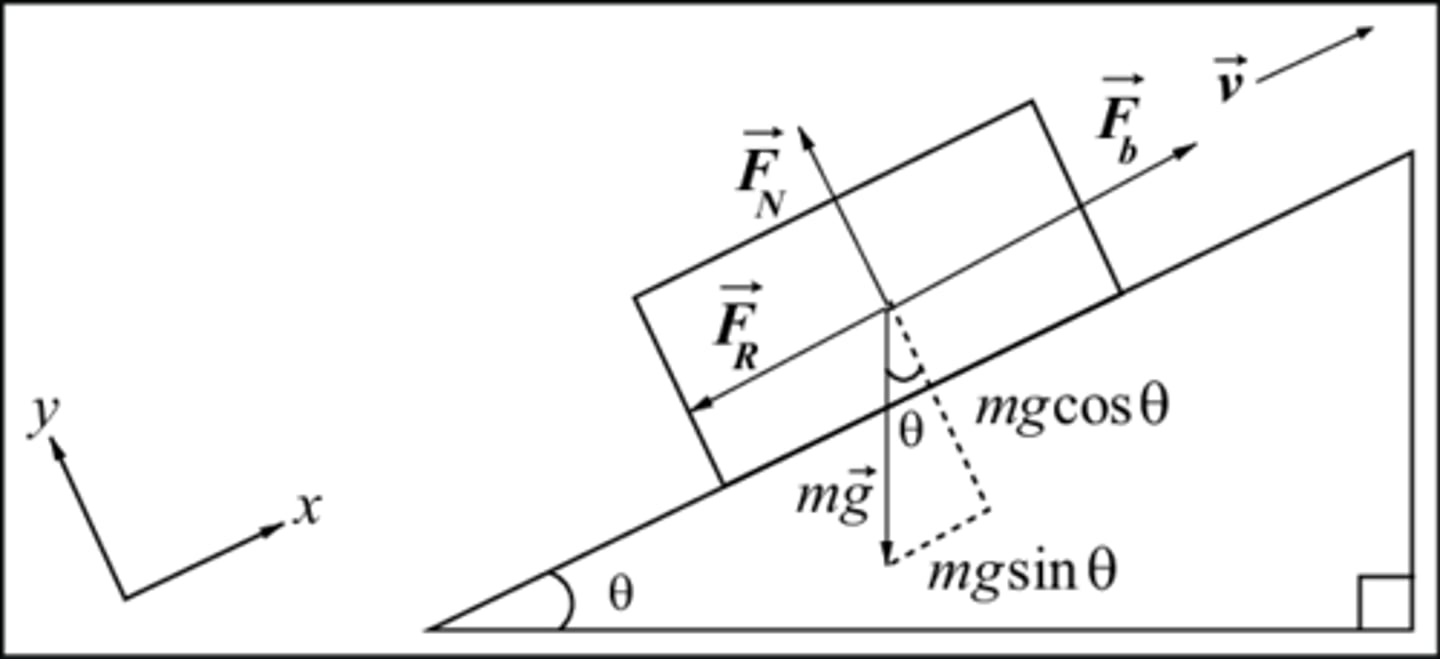
Inclined planes

are another example of two-dimensional movement. it is often easiest to consider the dimensions as being parallel and perpendicular to the surface of the plane.

Describe the force diagram of an object on an inclined plane?

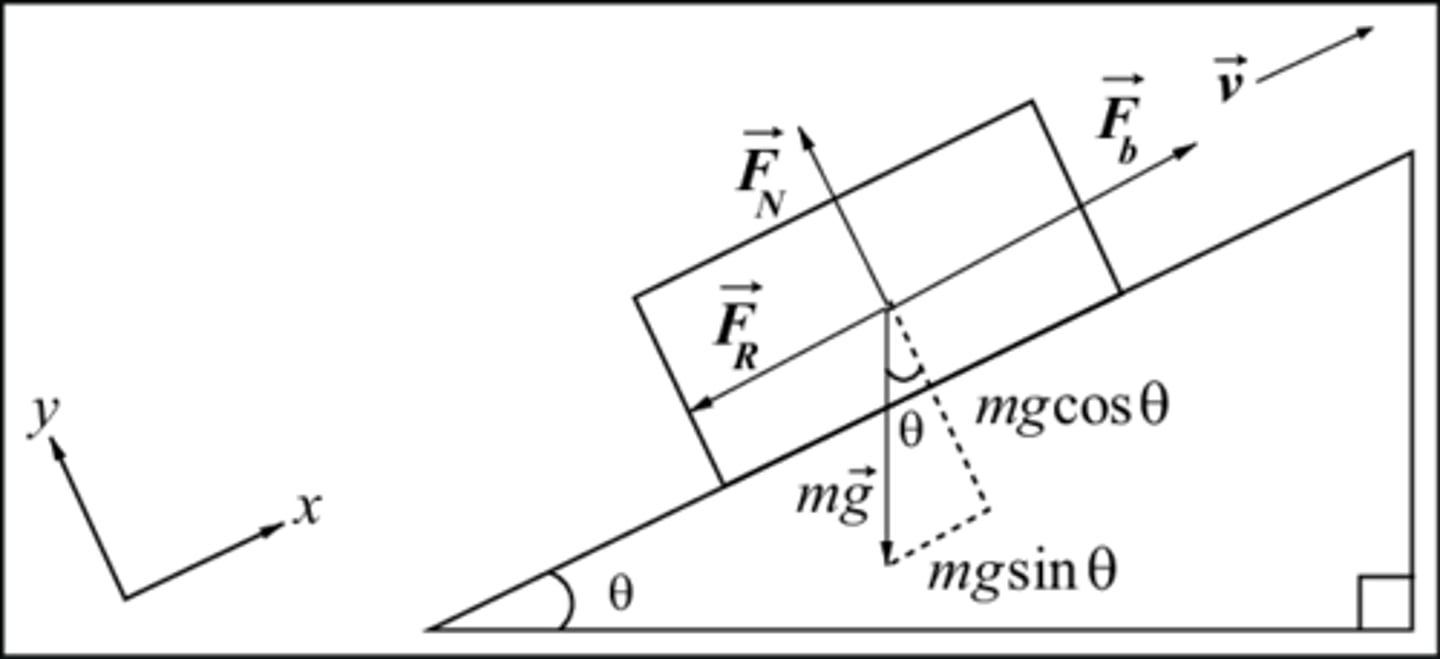
Fg,|| =

Fg,|_ =

mgsinθ [parallel]

mgcosθ [perpendicular]

Fg,|| : is the component of gravity parallel to the plane (oriented down the plane)

Fg, _| : is the component of gravity perpendicular to the plane (oriented into the plane)

m: mass

g: acceleration due to gravity

θ: angle of incline

What is the force of acceleration on an inclined plane?

gsin(theta)

Circular motion

occurs when forces cause an object to move in a circular pathway.

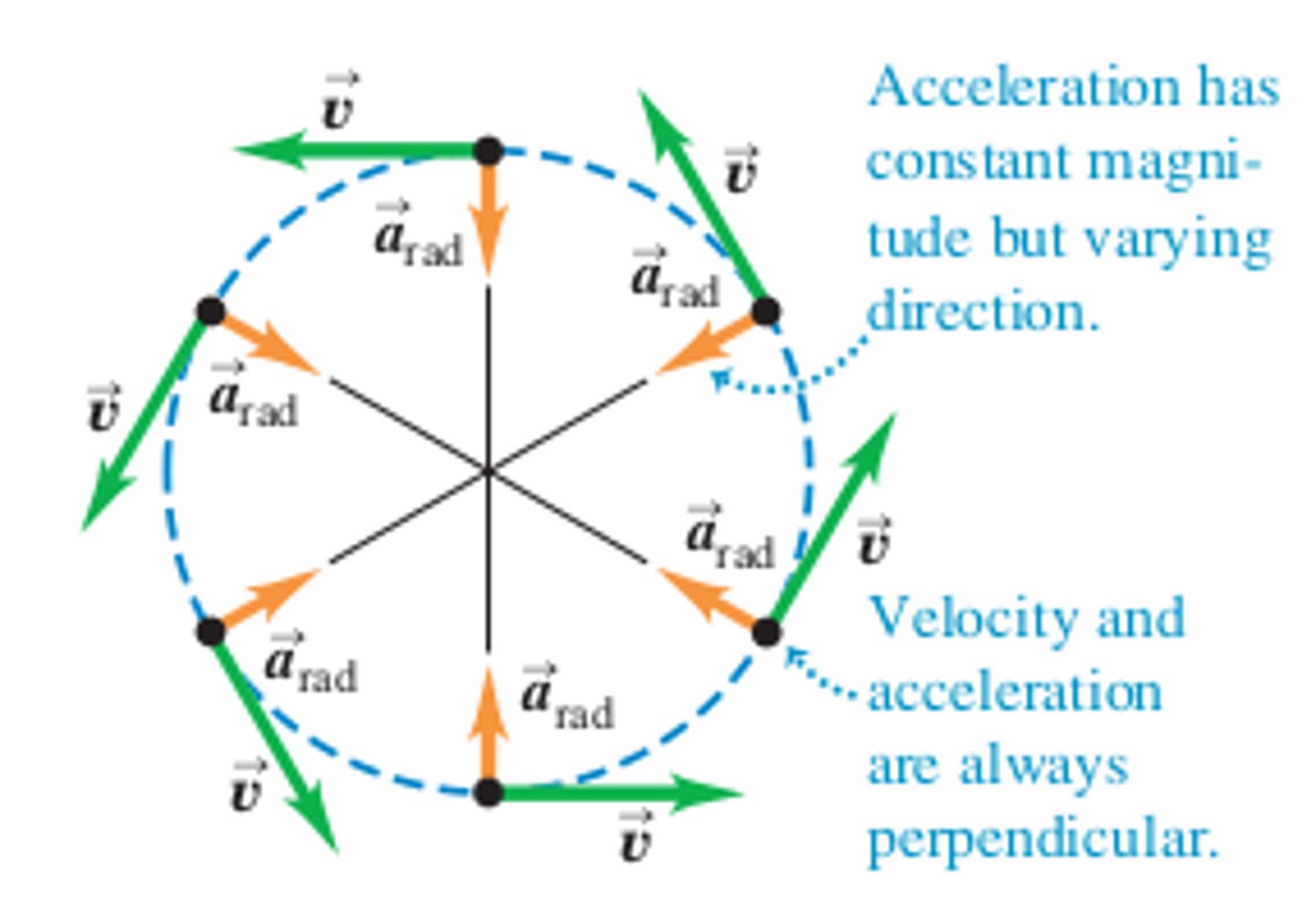
Uniform circular motion

the only force is the centripetal force, pointing radially inward. The instantaneous velocity vector always points tangentially.

in uniform circular motion, the instantaneous velocity vector is always tangent to the circular path

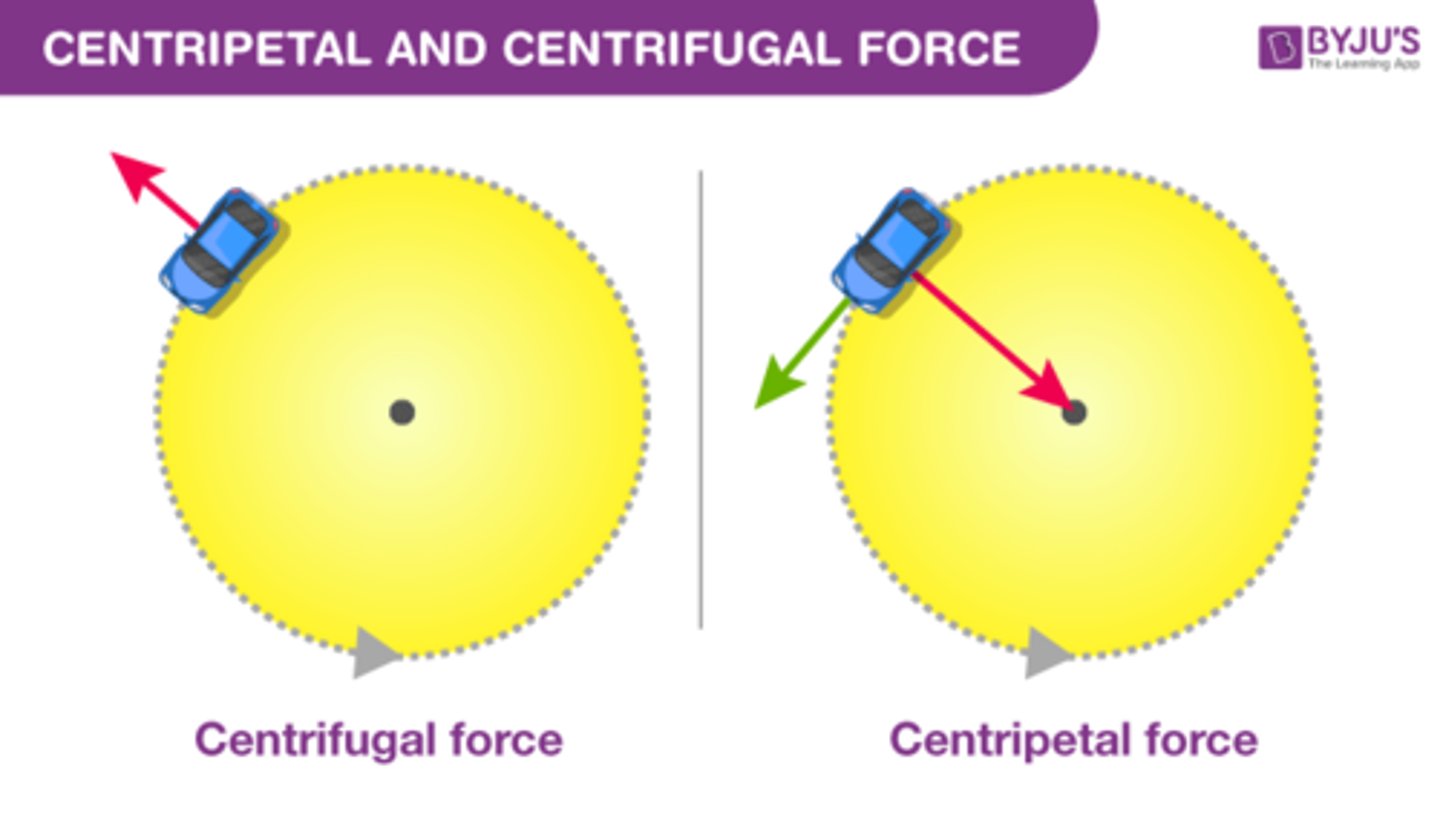
centripetal force

a force which always points radially inward

An equation that describes circular motion is

Fc = (mv^2)/r

m: mass

v : speed

r: radius of the circular path,

air resistance

like friction, opposed the motion of an object.

air resistance increases as the speed of the object increases.

therefore, objects in free fall will experience an increasing drag force as the magnitude of the velocity increases.

The amount of time it takes for an object to get to its maximum height is equivalent to

the time it takes for the object to fall back down to the starting height.(assuming air resistance is negligible)

terminal velocity

when an object is in free fall and the drag force biomes equal in magnitude to the weight of the object, and the object will then fall with constant velocity according to Newton's first law.

Translational Equilibrium

occurs in the absence of any net forces acting on an object. An object in translational equilibrium has a constant velocity, and may or may not also be in rotational equilibrium.

-exists only when the vector sum of all the forces acting on an object is zero.

Rotational equilibrium

occurs in the absence of any net torques acting on an object. Rotational motion may consider any pivot point, but the center of mass is most common. An object in rotational equilibrium has a constant angular velocity, On the MCAT the angular velocity is usually 0.

-exists only when the vector sum of all the torques acting on an object is zero.

first condition of equilibrium

simple a reiteration of Newton's First Law:

states that an object will remain at rest or move with a constant velocity if there is no net force on the object

Second condition of equilibrium

when the vector sum of all the torques acting on an object is zero.

fulcrum

the fixed pivot point around which an object rotates.

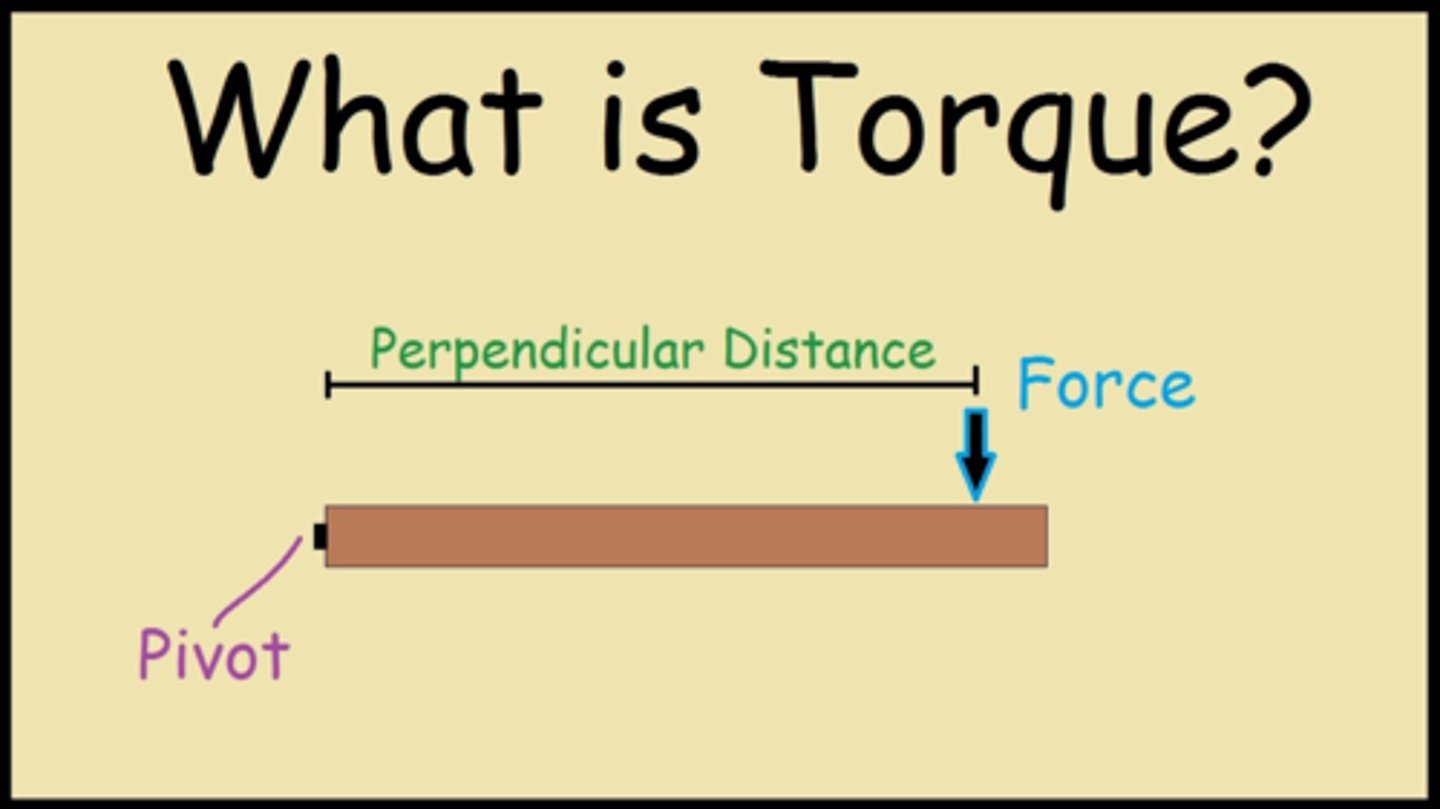
Torque

application of force at some distance from the fulcrum generates torque or the moment of force.

-generate rotational motion.

the equation for torque is a cross product:

T = r x F = rFsinθ

r: length of the lever arm

F: is the magnitude of the force

θ: the angle between the lever arm and the force vectors.

torques that generate clockwise motion are considered_______

torques that generate counterclockwise rotation are considered___________

Negative

positive

lever arm

the distance between the applied force and the fulcrum is termed the lever arm

Rotational motion

-occurs when forces applied against an object in such a way as to cause the object to rotate around a fixed pivot point

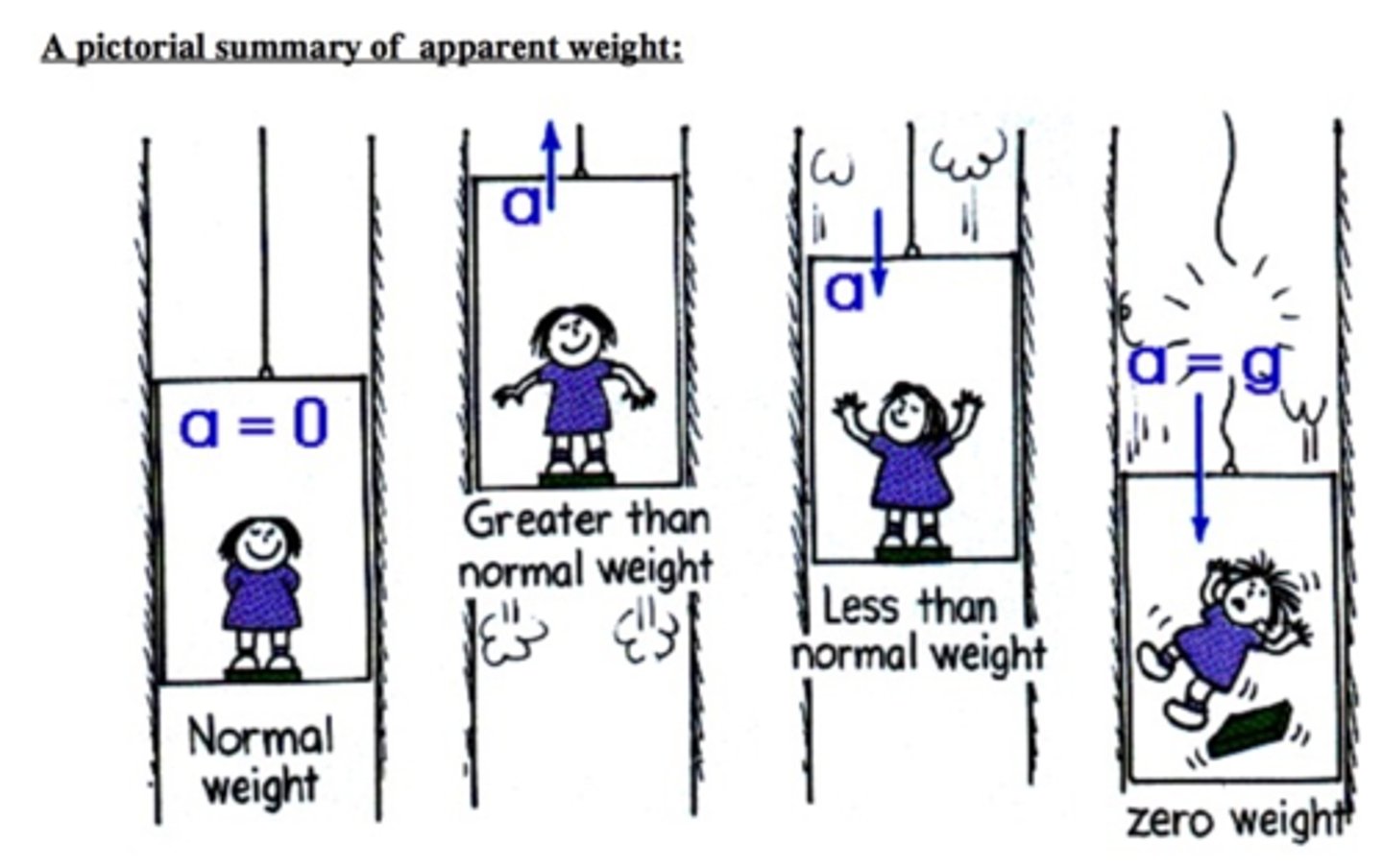
Describe the force diagram for an elevator moving at constant speed?

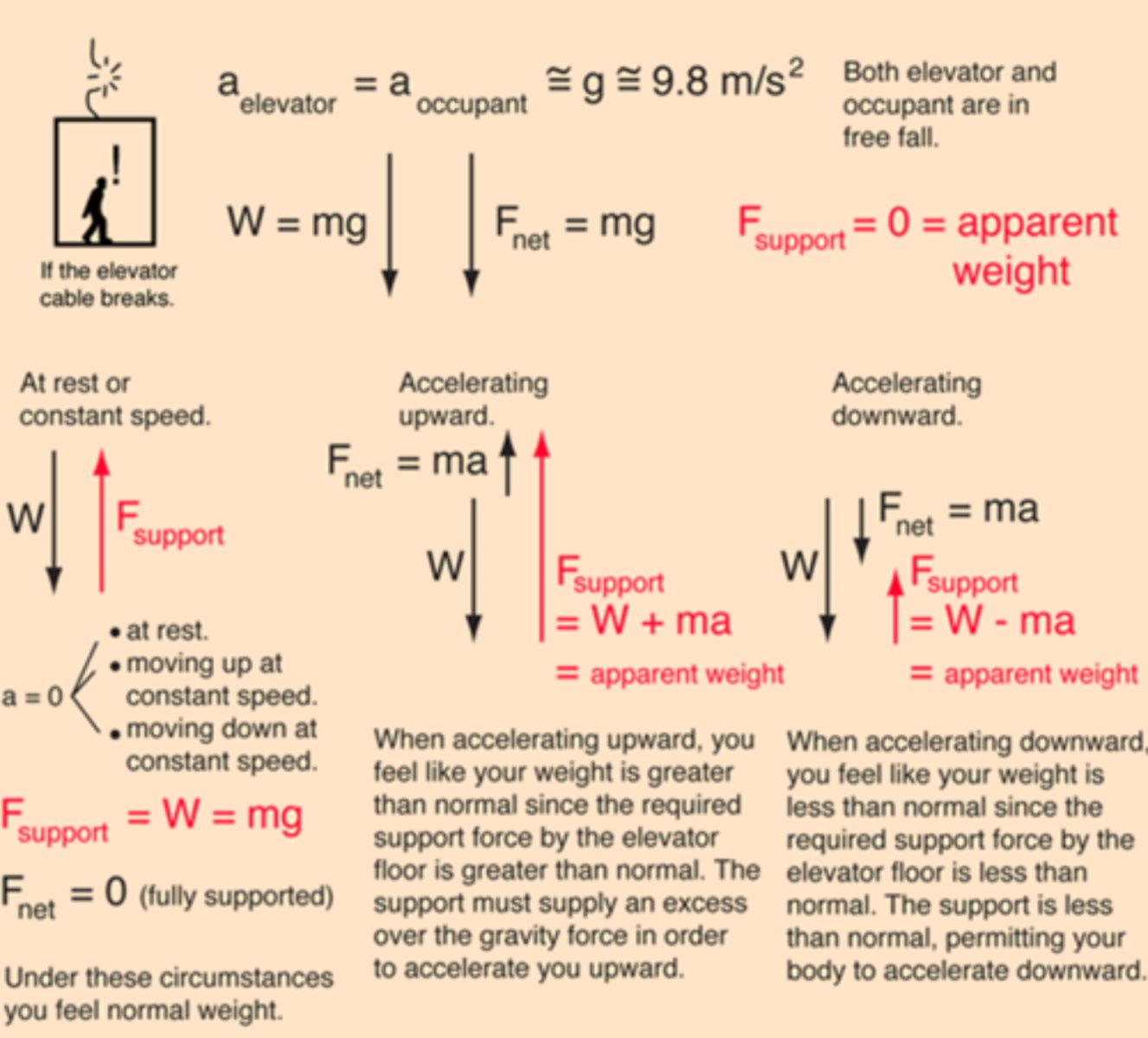
Describe the force diagram for an elevator accelerating upward?

Describe the force diagram for an elevator accelerating downward?

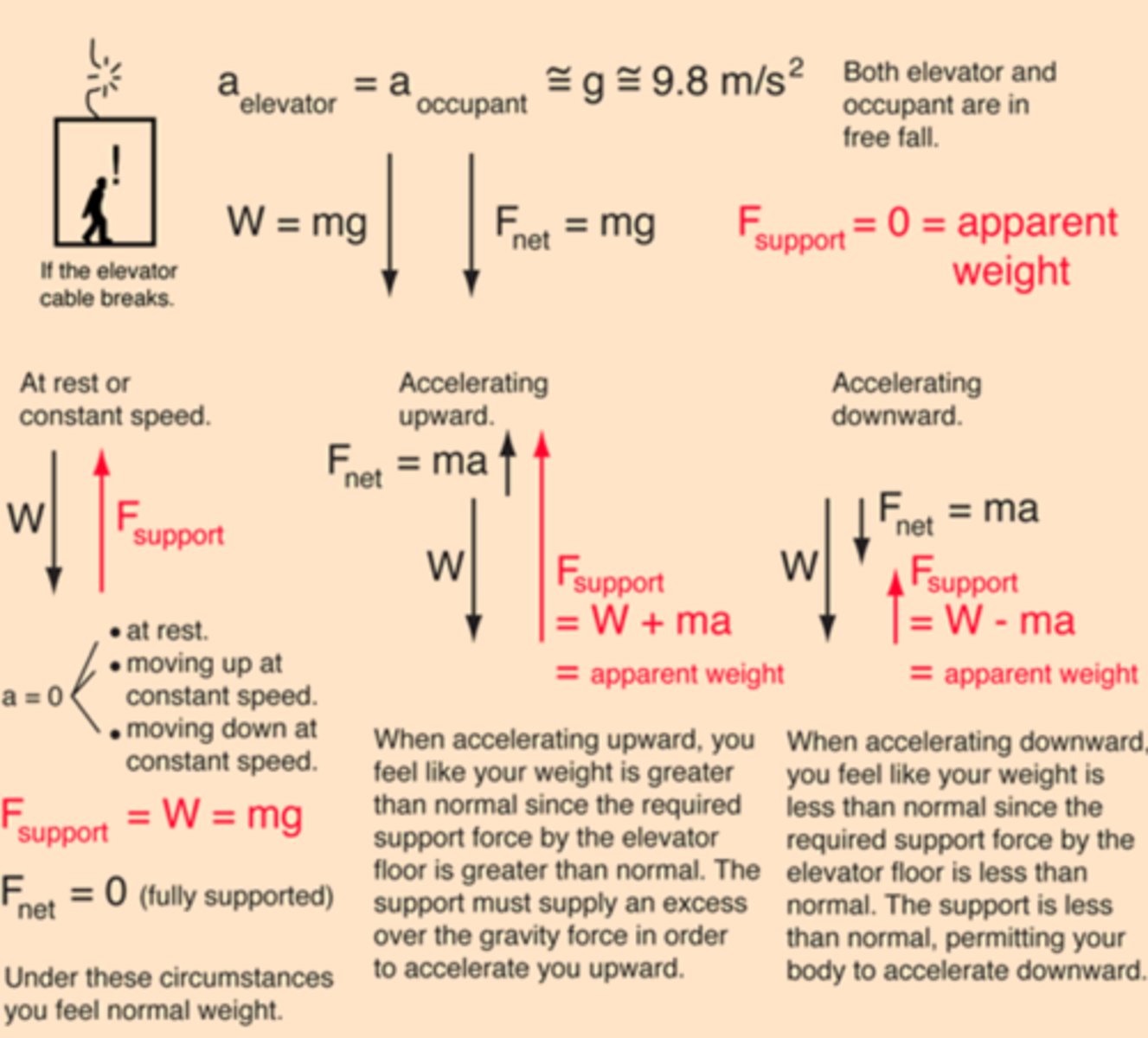
Describe the force diagram for an elevator deccelerating downward?

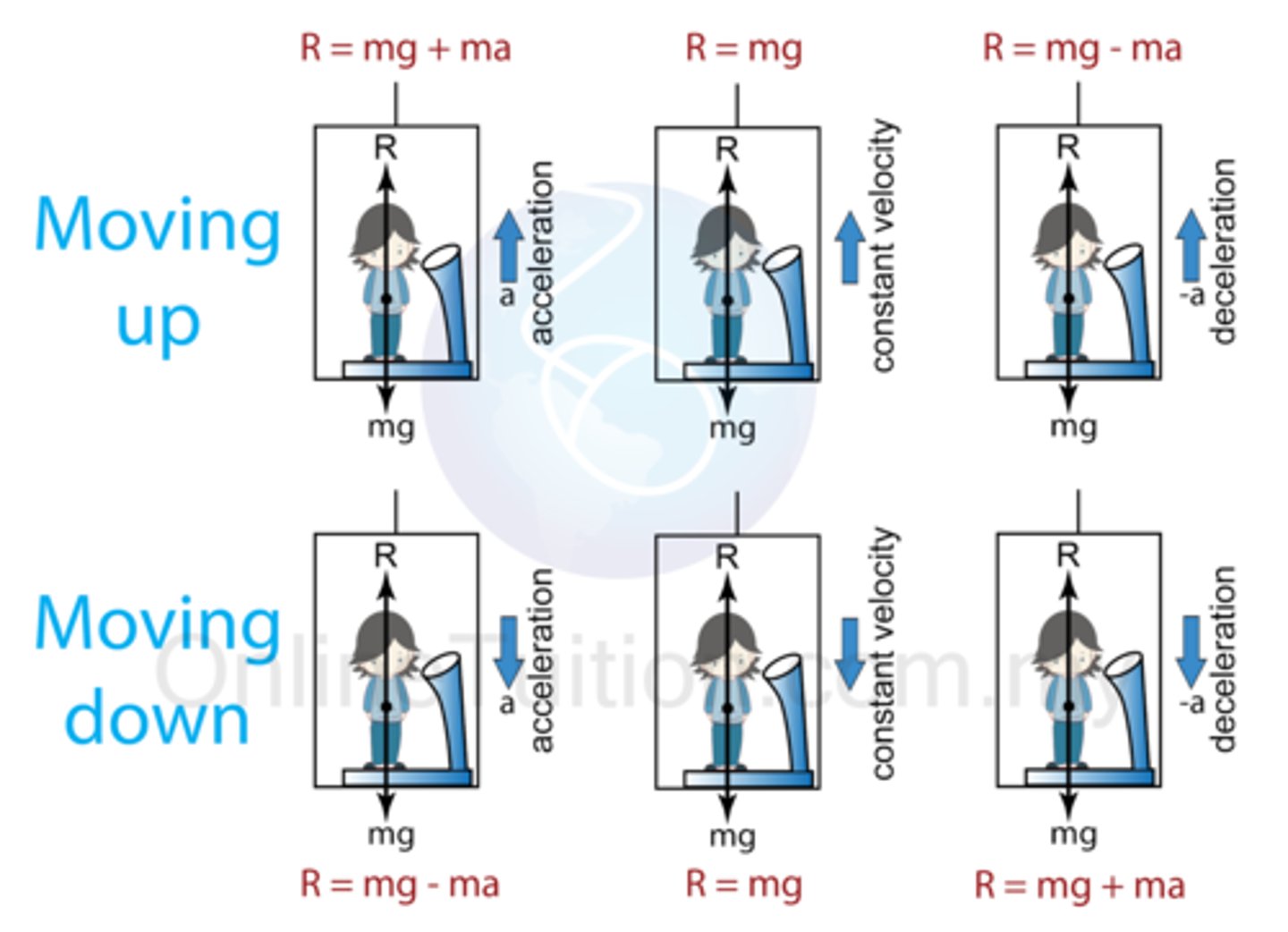
Describe what the scale reading would be if a person was in an elevator accelerating? decelerating? the wire was cut? a = 0?

Tension

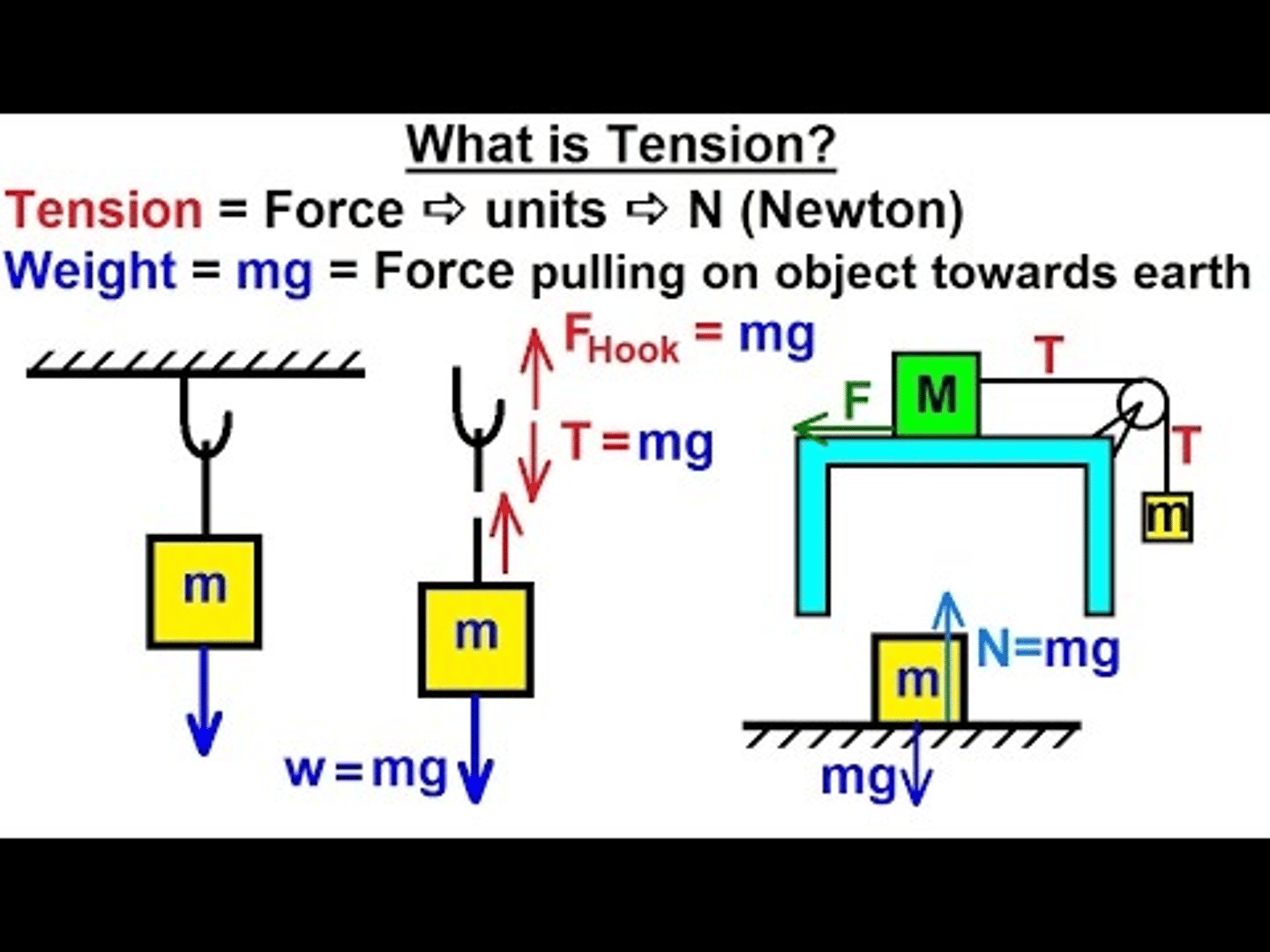
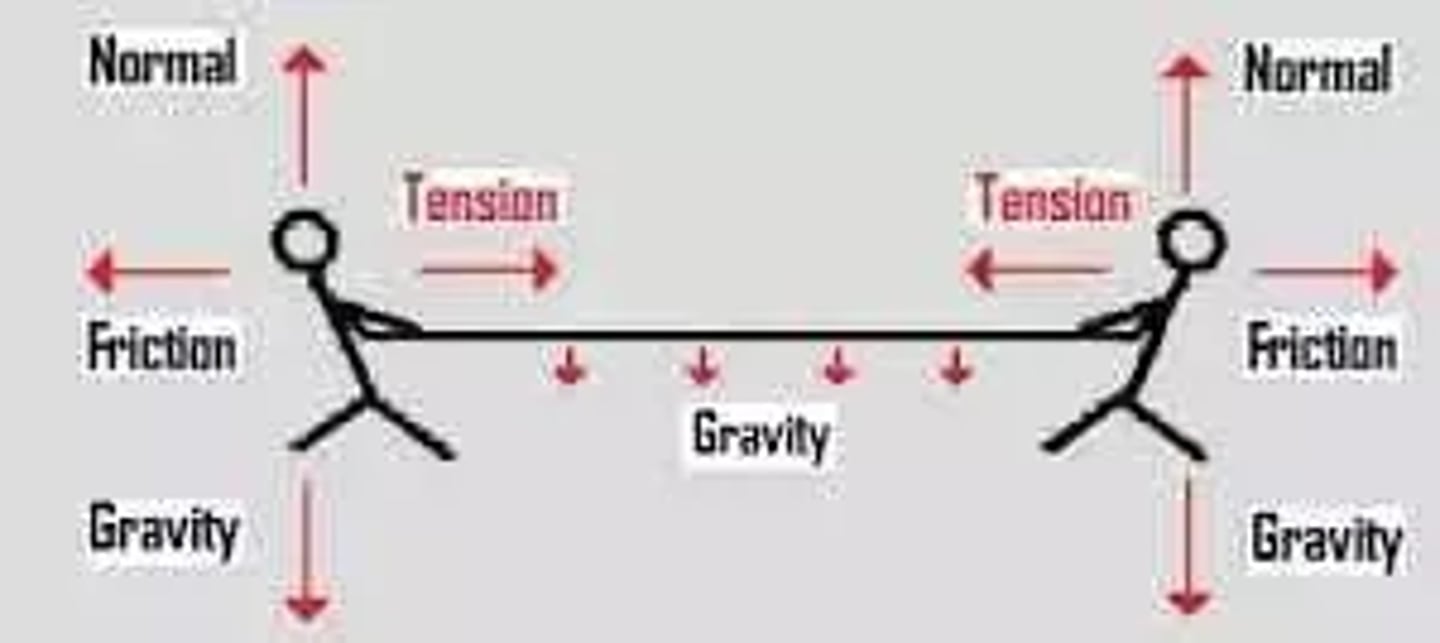
Describe the free body diagram of an object being held up by two strings in opposite directions

What is the tension of a rope of someone pulling it with a tree at the other end?

0N

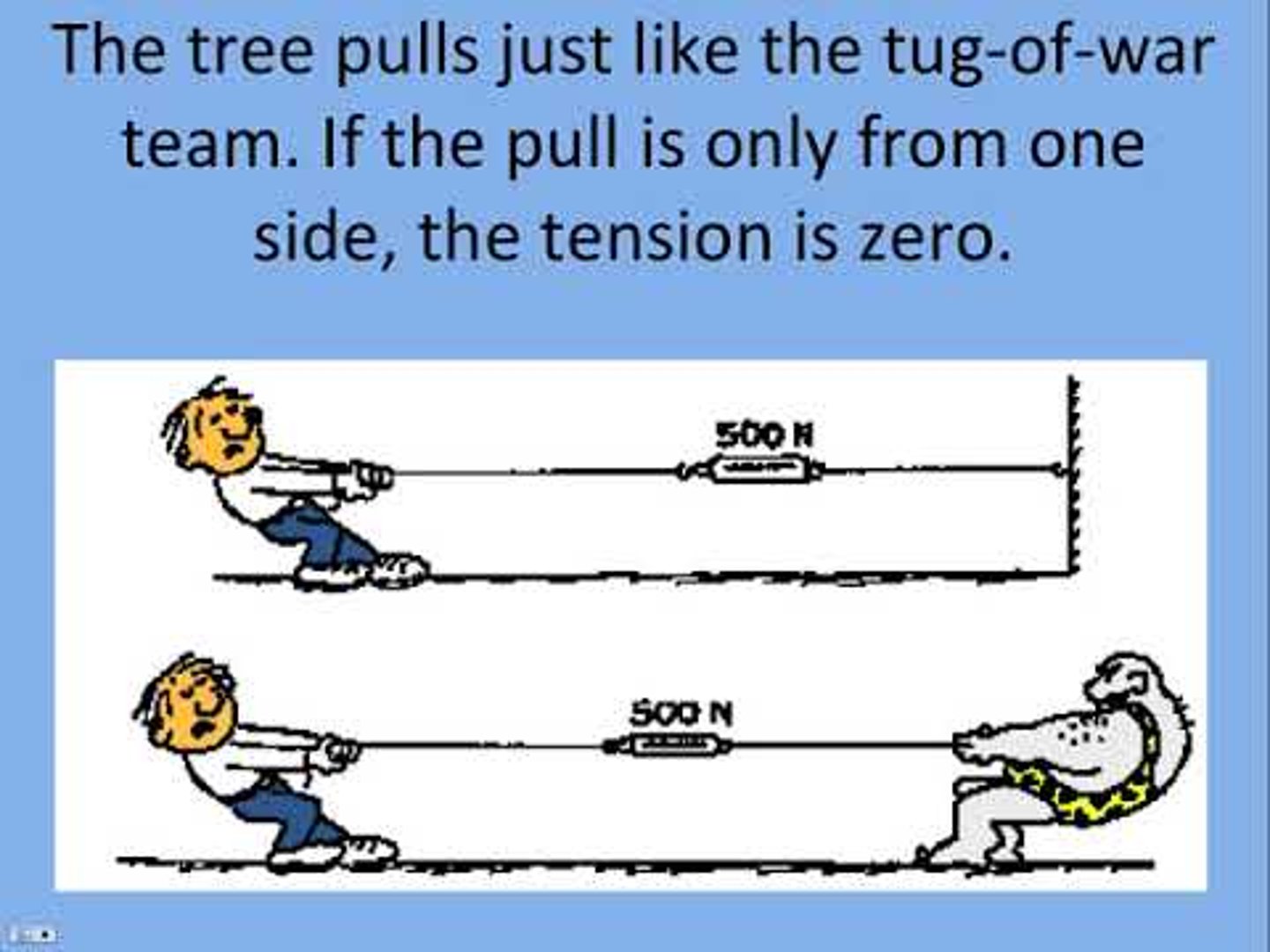
What is the tension of the rope during a tug of war, one team pulls it left by 75N and the other team pulls it by 70N?

70N

Tension is determined by the weaker of two forces. A helpful way to think about it is considering that if only one side of the rope is pulled, the tension in the rope is zero. It's only by having a weaker opposing force that tension is created.