AP Calc AB - Chapter 1

Limits and Their Properties

An even function is…

An even function is…

symmetric w/ respect to y-axis like:

• y=x²

• y=cos x

• y=|x|

f(-x)=f(x)

An odd function is…

symmetric w/ respect to origin like”

• y=x³

• y=sin x

• y=tan x

f(-x)=-f(x)

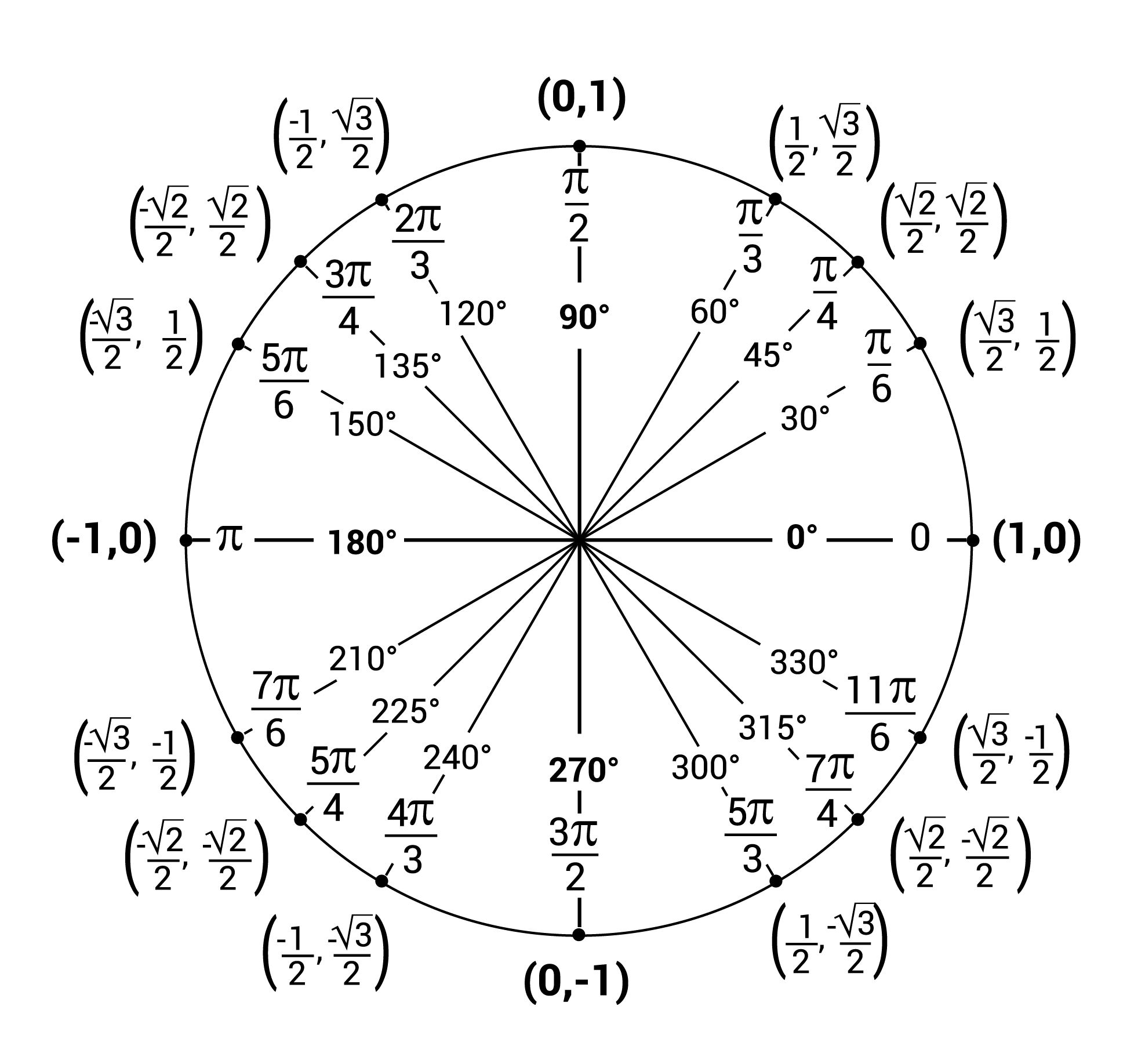
Unit Circle

Point-slope form of linear equation

y - y1 = m(x - x1)

Ways to solve limits algebraically

1. Substitute directly

2. Factoring

3. Rationalize w/ conjugate

4. LCM

5. Apply trig identities for trig limits

Two Special Trig Limits

• lim of sin x/x = 1 as x→0

• lim of (1-cos x)/x = 0 as x→0

• *lim of tan x/x = 1 as x→0

The Sanwich/Squeeze Theorem

If h(x) is less than or equal to f(x) which is less than or equal to g(x), all x in open interval containing c:

lim of h(x) = L = lim as x→x g(x) as x→c, then

lim of f(x) as x→c exists & = L

Continuity Test

Function f(x) is continuous at x = c if & only if it meets three conditions:

1. f(c) exists (c lies in domain f)

2. lim of f(x) as x→c exists (f has limit x→c)

3. lim of f(x) as x→c = f(c) (limit = function value)

Limits that DNE (do not exist)

• lim of f(x) as x→c from the left is not equal to lim of f(x) as x→c from the right

• f(x) goes up or down w/o bound

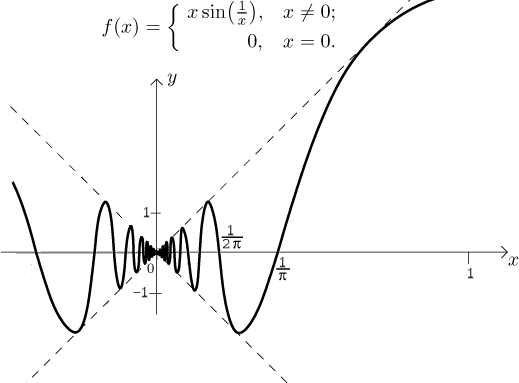
• f(x) oscillates between two fixed values as x→c (shown in image)

Types of Discontinuity

3 types:

1. Jump (nonremovable)

2. Infinite (nonremovable)

3. Point (removable)

Intermediate Value Theorem

Suppose f continuous on closed interval [a,b]. Let w be any number strictly between f(a) and f(b). Then there exists #c in (a,b) such that f(c)=w.

1. Identify if function’s continuous

2. Plug intervals into equation

3. See if f(c) is between f(a) and f(b)

Limits Involving Infinity

2 types:

1. lim of f(x) as x→±infinity = #, infinity

2. lim of f(x) as x→c = infinity

Limits w/ Infinity Rules

y = ax^m/bx^n

• Degree of numerator larger (m>n), no horizontal asymptote, limit of f(x) as x→±infinity = DNE (does not exist)

• Denominator’s larger (m<n), horizontal asymptote: y=0, limit of f(x) as x→±infinity = 0

• Degrees are the same (m=n), ratio between leading coefficients, lim of f(x) as x→±infinity = a/b

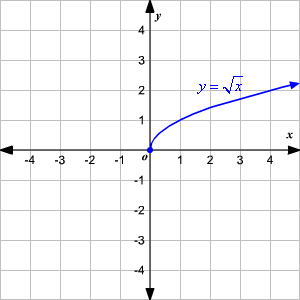
Graph of y=square root of x

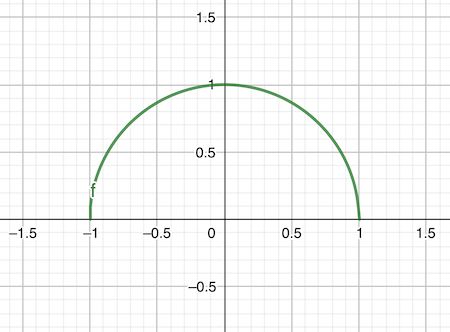
Graph of y=square root of 1-x²

Graph of y=|x|

*Absolute Value Function

Graph of y=ln x

*Natural Log Function

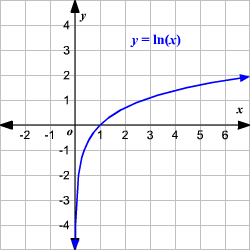
Graph of y=e^x

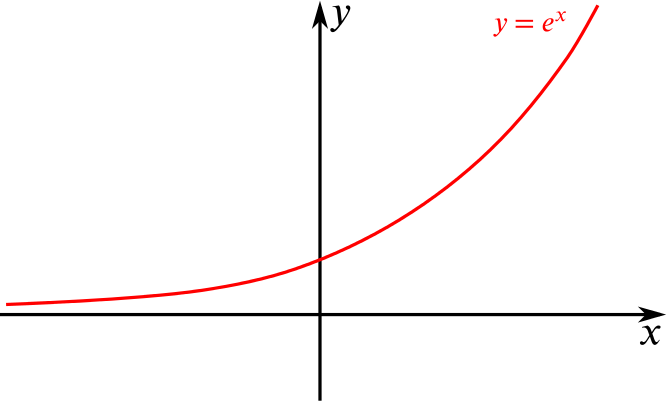
Graph of y=1/x

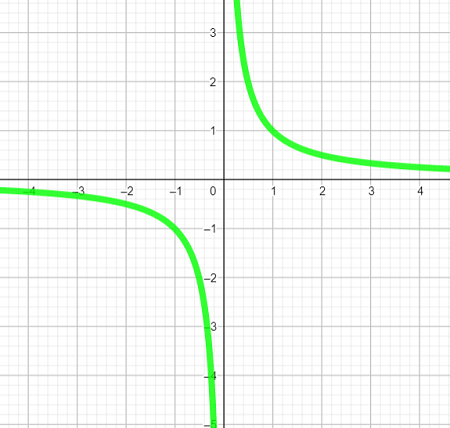
Graph of y=sec x

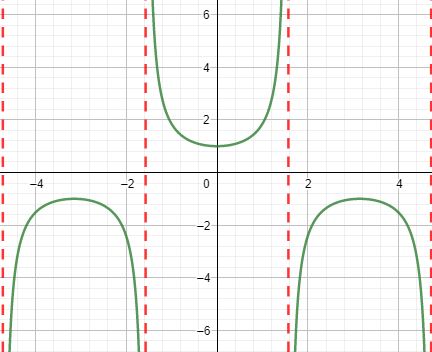
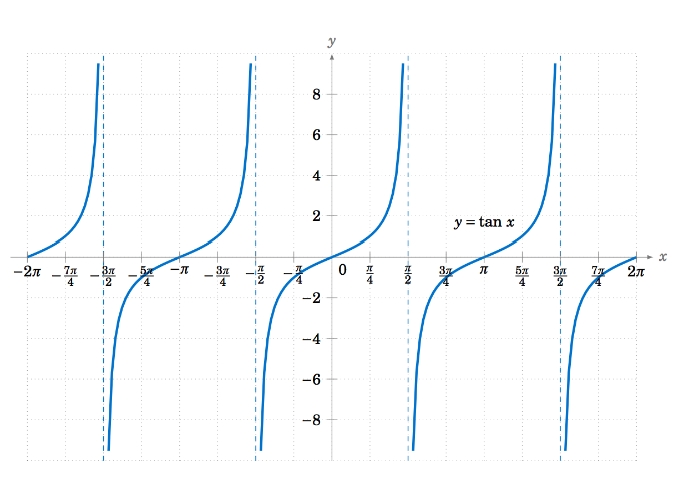
Graph of y=tan x

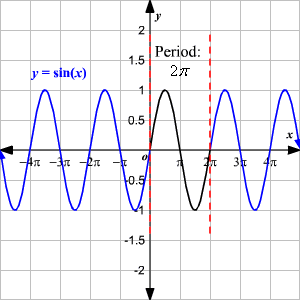
Graph of y=sin x

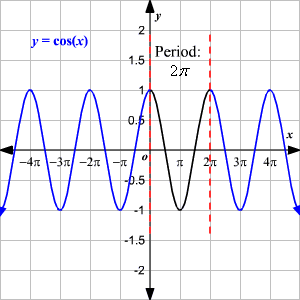
Graph of y=cos x

Graph of y=csc x

Graph of y=cot x

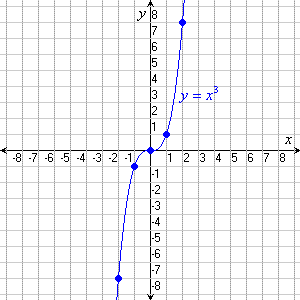
Graph of y=x³

*Cubic Function

Greatest Integer Function

f(x) = [[x]]