AC/DC Circuits - My edit

Ohm's law

Current flowing through a conductor is proportional to the voltage across it, given a constant physical condition

dB conversion

= 10log₁₀(P_out / P_in) == 20log₁₀(V_out / V_in)

State Kirchoff's 2 laws

1st law (KCL): Algebraic sum of currents going into and out of a junction must equal 0A.

2nd law (KVL): The sum of EMFs in a circuit equals the sum of potential drops.

The superposition theorem

Definition:
The response of any linear branch or linear circuit with multiple EMFs or current sources, is the same as the sum of the response of each individual EMF while all other source is replaced by its internal resistance (r).

1. Voltage source is Open-circuited

2. Current source is Short-circuited

Thevenin's theorem

States that a linear two-terminal circuit can be replaced by an equivalent circuit consisting of a voltage source V_Th in series with a resistor R_Th, where V_Th is the open-circuit voltage at the terminals and R_Th is the input or equivalent resistance at the terminals when the independent sources are turned off.

Norton's theorem

Any network of voltage or current sources and resistors is electrically equivalent to an ideal current source in parallel with a single resistor.

Conductance (G)

How easily current flows through a specific object

Unit: Siemens (S)

I/V = 1/R {S}

Conductivity (σ)

A materials inherent ability to conduct. Unit: Siemens per metre (Sm^-1)

σ = 1/ρ {Sm^-1}

When is the supermesh technique used?

when a current source is shared between 2 loops

Good current source vs Good voltage source

A good current source supplies a constant current irrespective of the load

A good voltage source supplies a constant voltage irrespective of the load

Phase angle (△Φ)

Determines where the peak of the sinusoidal function is relative to standard sine wave.

△t = -△Φ/ω

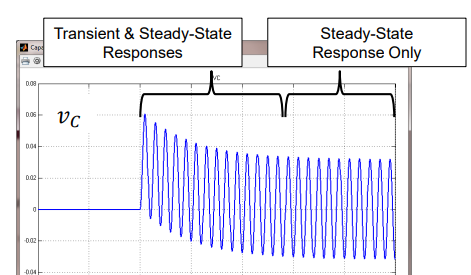
Steady-State Response

Occurs when components have been driven for a while by a stable sinusoidal signal source.
The response of the circuit is also sinusoidal, and has the same frequency as the signal source.

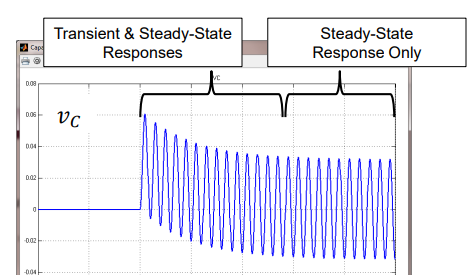
Transient Response

Occurs when the circuit is first switched on, alongside the steady-state response (SSR) and is not stable.
Occurs for a finite period of time.
Frequency of response is still the same as the source frequency.

A Phasor

A way to represent the magnitude and phase of a signal in a linear circuit.
Denoted by a capital. Eg; V, I…

v = V_mcos(ωt + Φ)
V = V_me^jΦ = V_m∠Φ

Cut-off frequency (for an RC circuit)

ω_c = 1/RC

f_c = 1/2πRC

Definition:
The frequency at which the transfer function’s magnitude decreases by a factor of 1/√2 of its maximum.

Resonant frequency (ω₀)

ω₀ = 1/√(LC)

f₀ = 1/2π√(LC)

Definition:

Resonant frequency is the frequency when the magnitude of a circuit’s transfer function is at its maximum value, and when the circuit has no overall reactance.

Bandwidth (B / rad s^-1)

B = ω_c2 - ω_c1
B = R / L

The bandwidth is symmetrical around the resonant frequency (ω₀).
Thus, we can add half the bandwidth to ω₀ to find ω_c1 and ω_c2.

Definition:

The bandwidth is the range of frequencies surrounding the resonant frequency where the magnitude of the transfer function remains above 1/√2 of the maximum value.

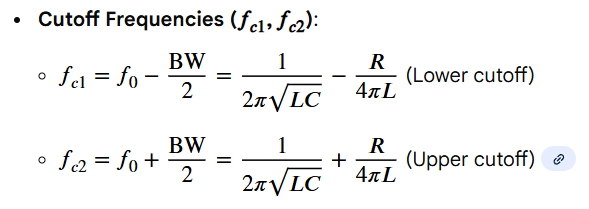
Q-factor

Q = ω₀ / B =ω₀ / (ω_c2 - ω_c1)

Definition:

The ratio between the resonant frequency and the bandwidth of a circuit

Inductance (L / H)

v = L * (di/dt)

Inductance = L (Units: Henrys {H})

Capacitance (C / F)

i = C * (dv / dt)

C = Q/v

C = εA/d

Capacitance = C (Units: Farads {F})

Maximum Power Transfer Theorem (Part 2)

R_L = R_S —> Z_L = Z_S^*

Impedance is a complex value, so the real and imaginary parts behave differently.
For maximum power to the load:

R_L = R_S and X_L = -X_s