Polar Graphs
5.0(2)
5.0(2)
Card Sorting
1/19
Earn XP
Description and Tags
all coordinates are in polar form unless noted, take all graphs with a grain of salt because the graphs may ask for ask horizontal or vertical shift that these equations do not consider
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
20 Terms
1
New cards
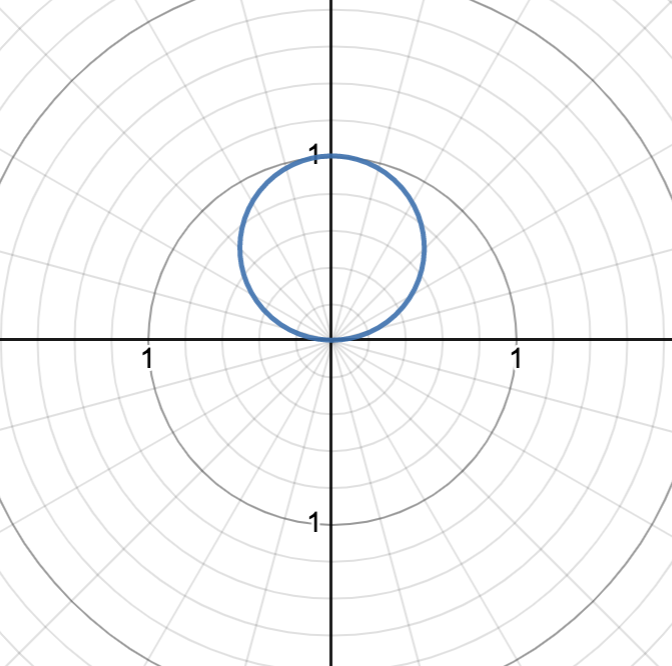
r = a sin(θ)
circle with diameter a, passing through the origin and (a, π/2), b is
graph pictured is r = sin(θ)
graph pictured is r = sin(θ)
2
New cards
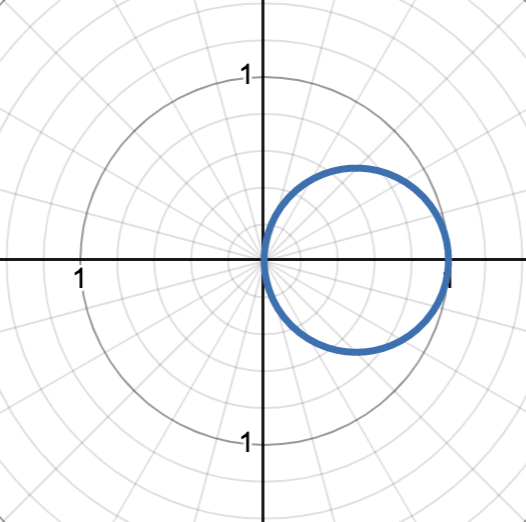
r = a cos(θ)
circle with diameter a, passing through the origin and (a, 0˚)
graph pictured is r = cos(θ)
graph pictured is r = cos(θ)
3
New cards
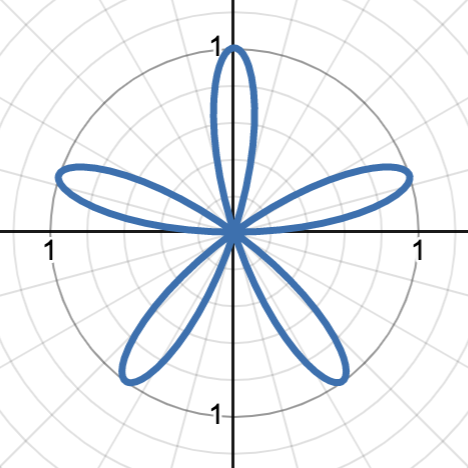
r = a sin(nθ), n is odd
rose curve with n as the number of petals around the origin and a as the amplitude of the petals. graph starts at the origin, graph is rotated 90˚ from cosine rose curve, negative graph will reflect around the polar axis
graph pictured is r = cos(5θ)
graph pictured is r = cos(5θ)
4
New cards
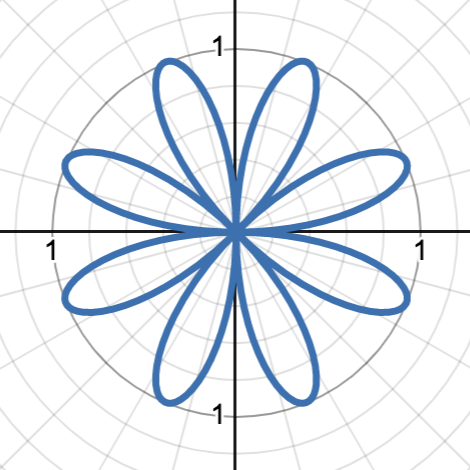
r = a sin(nθ), n is even
rose curve with 2n as the number of petals around the origin and a as the amplitude of the petals. graph starts at the origin, graph is rotated 90˚ from cosine rose curve
graph shows r = sin(4θ)
graph shows r = sin(4θ)
5
New cards
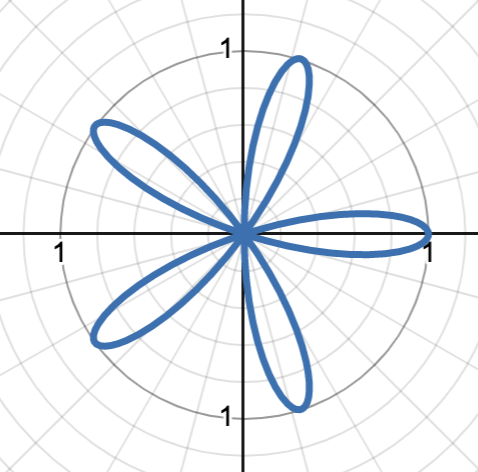
r = a cos(nθ), n is odd
rose curve with n as the number of petals around the origin and a as the amplitude of the petals. graph starts at the “peak“ of a petal, graph is rotated 90˚ from sine rose curve
graph pictured is r = cos(5θ)
graph pictured is r = cos(5θ)
6
New cards
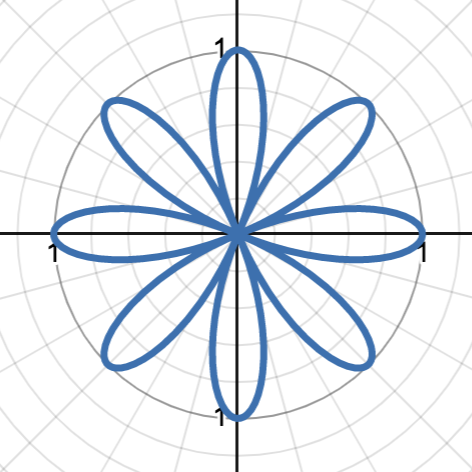
r = a cos(nθ), n is even number
rose curve with 2n as the number of petals around the origin and a as the amplitude of the petals. graph starts at the “peak“ of a petal, graph is rotated 90˚ from sine rose curve
graph shows r = cos(4θ)
graph shows r = cos(4θ)
7
New cards
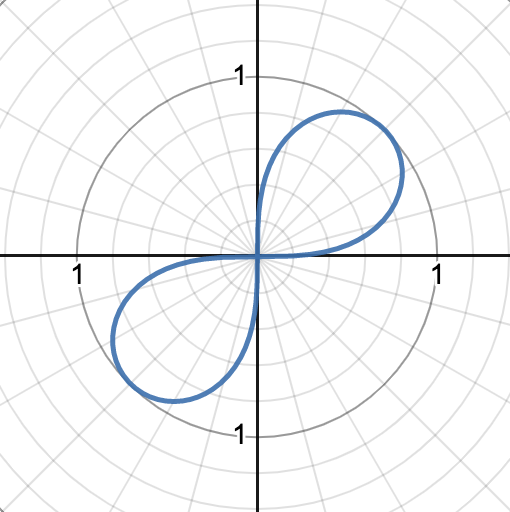
r^2 = a^2 sin(2θ)
lemniscate with both petals symmetric on the π/4 ray and a as the amplitude of the petals.
graph shows r^2 = sin(2θ)
graph shows r^2 = sin(2θ)
8
New cards
r^2 = a^2 cos(2θ)
lemniscate with both petals symmetric on the polar axis and a as the amplitude of the petals.
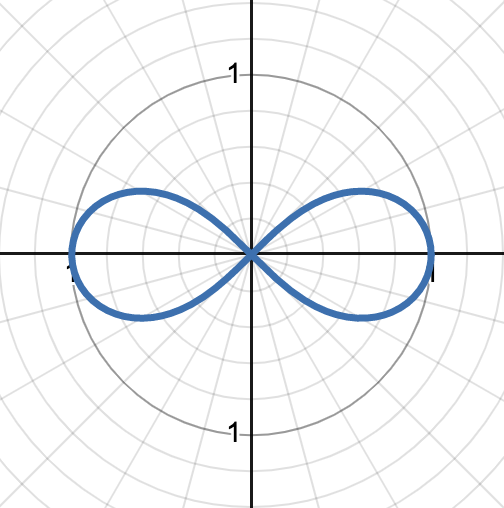
graph shows r^2 = cos(2θ)
graph shows r^2 = cos(2θ)
9
New cards
r = a ± b sin(θ), a/b < 1
looped limaçon symmetric about the π/2 ray, the amplitude of the “main” part of the limaçon is as tall as the positive part of the y = a ± b sin(x) graph, and the small loop is as tall as the negative part of the y = a ± b sin(x) graph, flipping sign of sin() will flip about the polar axis
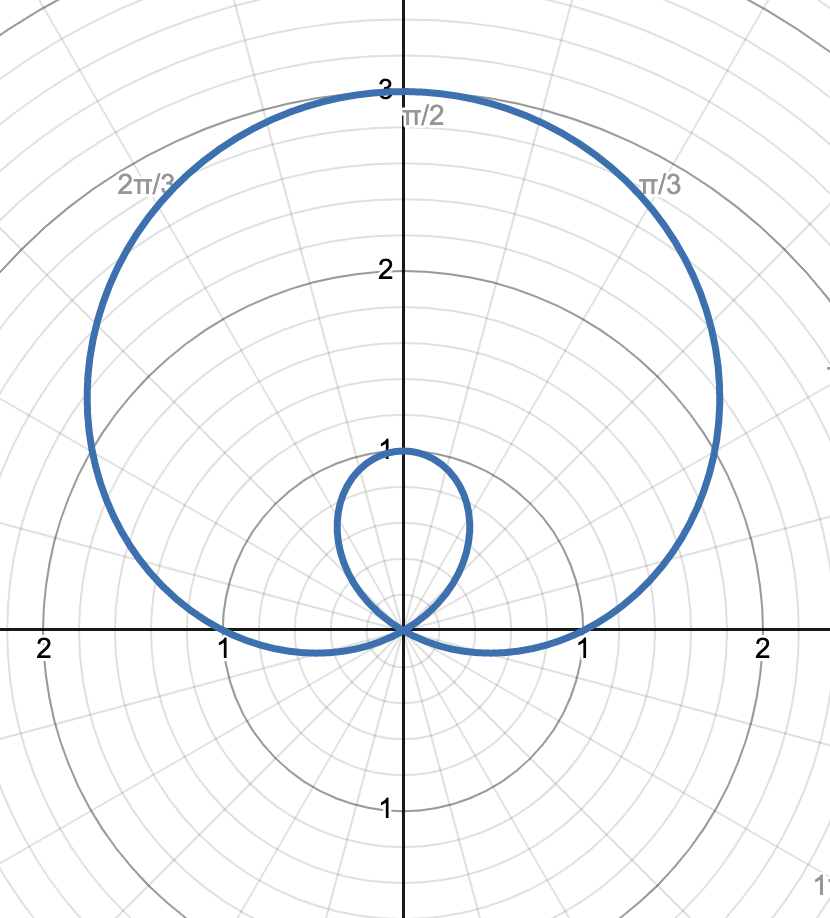
graph shows r = 1 + 2 sin(θ)
graph shows r = 1 + 2 sin(θ)
10
New cards
r = a ± b cos(θ), a/b < 1
looped limaçon symmetric about the polar axis, the amplitude of the “main” part of the limaçon is as tall as the positive part of the y = a ± b cos(x) graph, and the small loop is as tall as the negative part of the y = a ± b cos(x) graph, flipping sign of cos() will flip about the π/2 ray
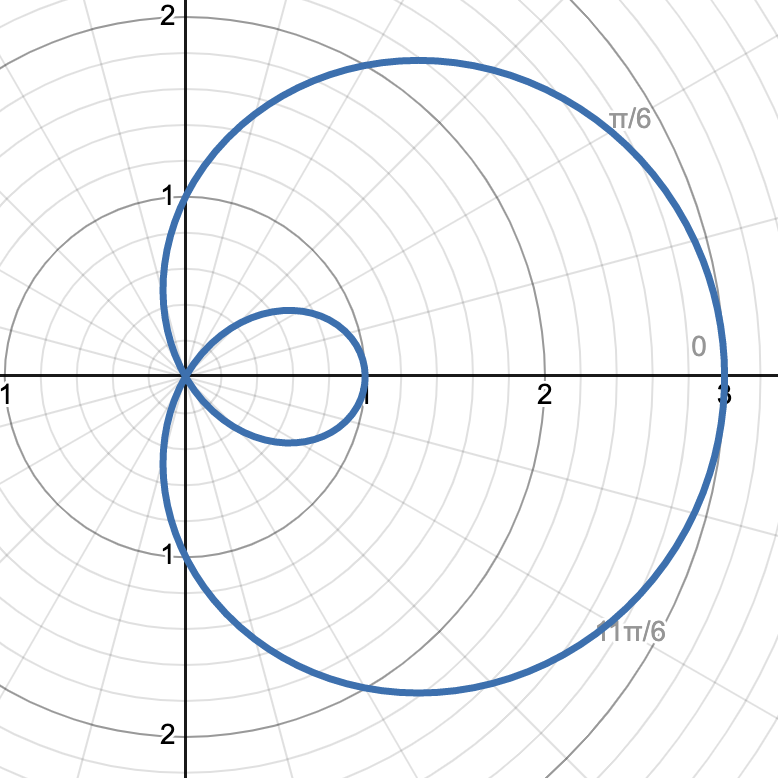
graph shows r = 1 + 2 cos(θ)
graph shows r = 1 + 2 cos(θ)
11
New cards
r = a ± b cos(θ), a/b = 1
cardioid/limaçon symmetric about the polar axis, the amplitude of the cardioid is 2a, point at the origin, flipping sign of cos() will flip about the π/2 ray
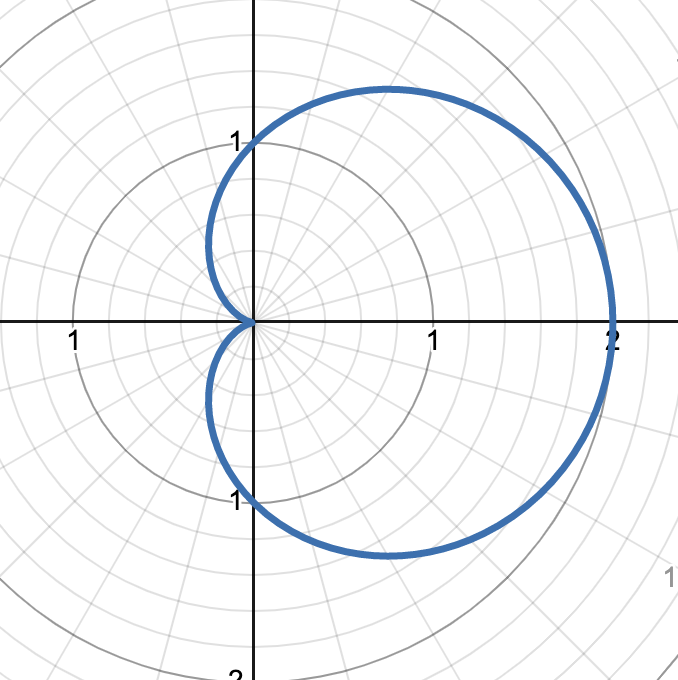
graph shows r = 1 + cos(θ)
graph shows r = 1 + cos(θ)
12
New cards
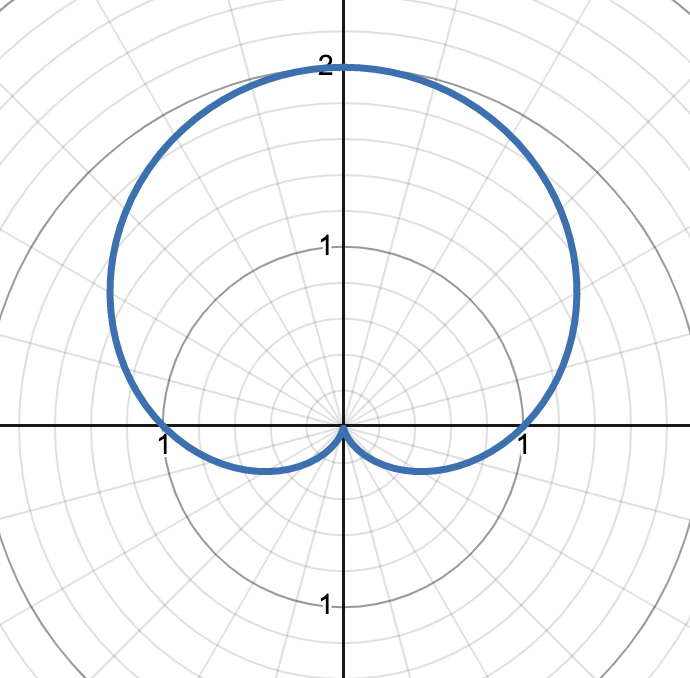
r = a ± b sin(θ), a/b = 1
cardioid/limaçon symmetric about the π/2 ray, the amplitude of the cardioid is 2a, point at the origin, flipping sign of sin() will flip about the polar axis
graph shows r = 1 + sin(θ)
graph shows r = 1 + sin(θ)
13
New cards
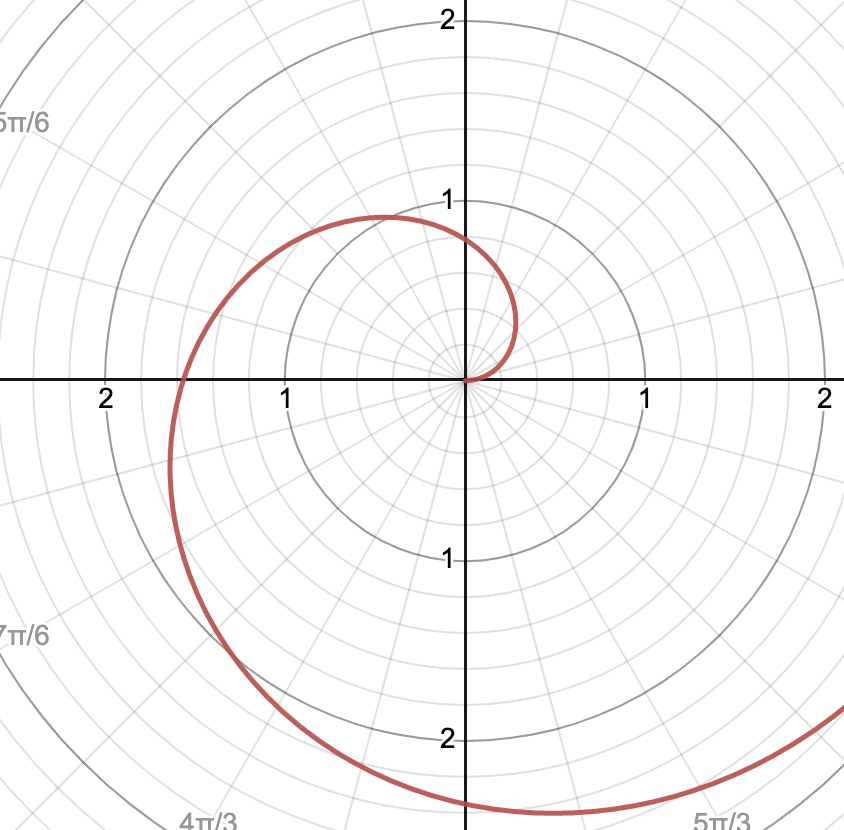
r = aθ
spiral of archimedes, starts at the origin and proceeds counter-clockwise if restricted to positive values and clockwise if restricted to negative values
graph shows r = θ/2, θ > 0
graph shows r = θ/2, θ > 0
14
New cards
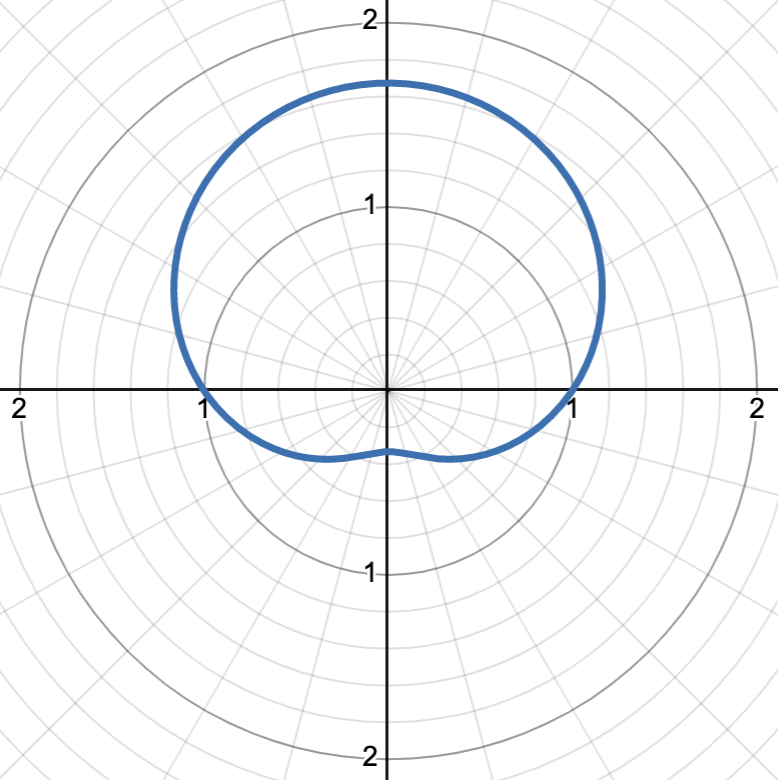
r = a ± b sin(θ), 1 < a/b < 2
dimpled limaçon, symmetric about the π/2 ray, the amplitude of the limaçon is “peak“ of graph, dimple at the closest value to r = 0, flipping sign of sin() will flip about the polar axis
graph is r = 1 + 2/3 sin(θ)
graph is r = 1 + 2/3 sin(θ)
15
New cards
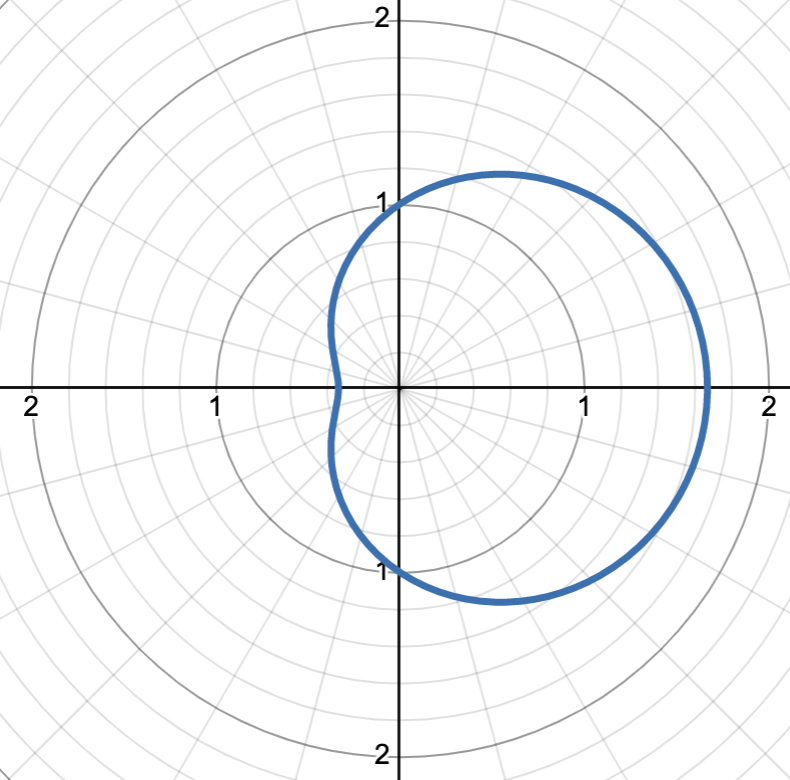
r = a ± b cos(θ), 1 < a/b < 2
dimpled limaçon, symmetric about the polar axis, the amplitude of the cardioid is 2a, dimple at the closest value to r = 0, flipping sign of sin() will flip about the π/2 ray
graph is r = 1 + 2/3 cos(θ)
graph is r = 1 + 2/3 cos(θ)
16
New cards
r = a ± b sin(θ), a/b ≥ 2
convex limaçon, symmetric about the π/2 ray, the amplitude of the limaçon is “peak“ of graph, flat part at the closest value to r = 0, flipping sign of sin() will flip about the polar axis
graph is r = 1 + 1/2 sin(θ)
graph is r = 1 + 1/2 sin(θ)
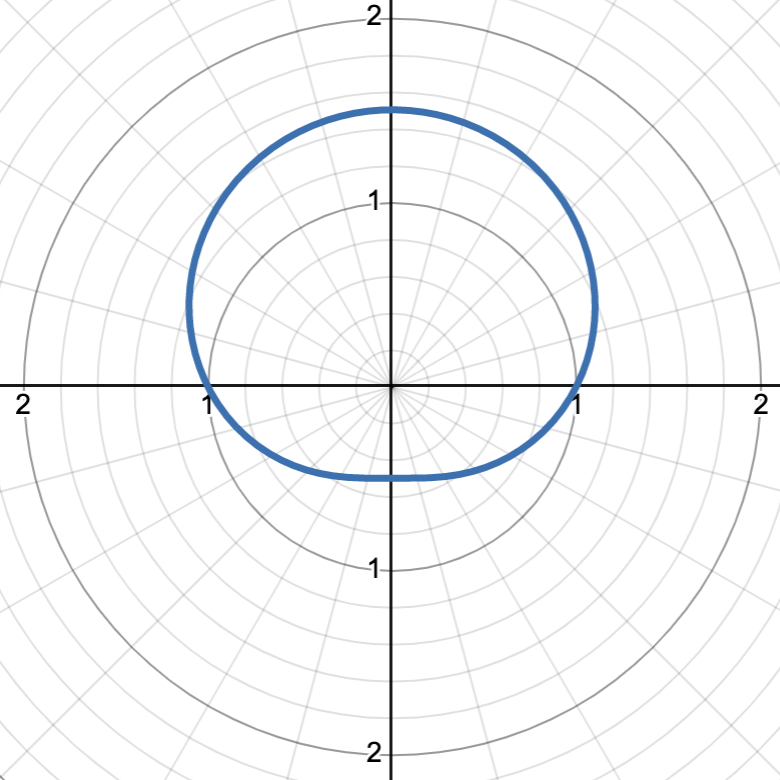
17
New cards
r = a ± b sin(θ), a/b ≥ 2
convex limaçon, symmetric about the polar axis, the amplitude of the limaçon is “peak“ of graph, flat part at the closest value to r = 0, flipping sign of sin() will flip about the π/2 ray
graph is r = 1 + 1/2 cos(θ)
graph is r = 1 + 1/2 cos(θ)
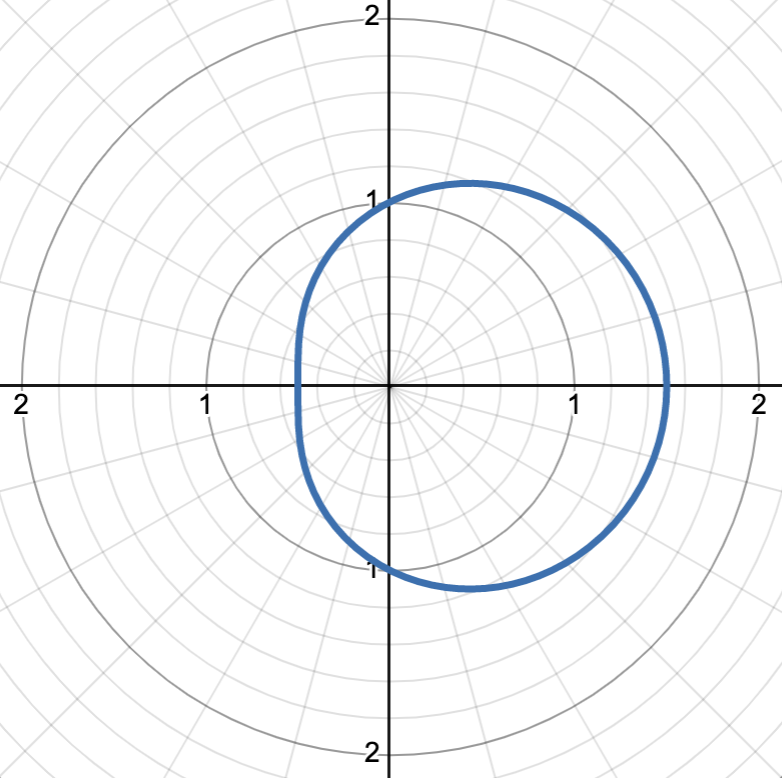
18
New cards
r = a + b sin(nθ) OR r = a + b cos(nθ), n is odd positive integer > 1, b > a
rose curve with petals inside of the main petals, amplitude of both petals determined by value of b - a (small petal) and b + a (big petal), 2n is the number of petals
graph shows r = 1/2 + sin(3θ)
graph shows r = 1/2 + sin(3θ)
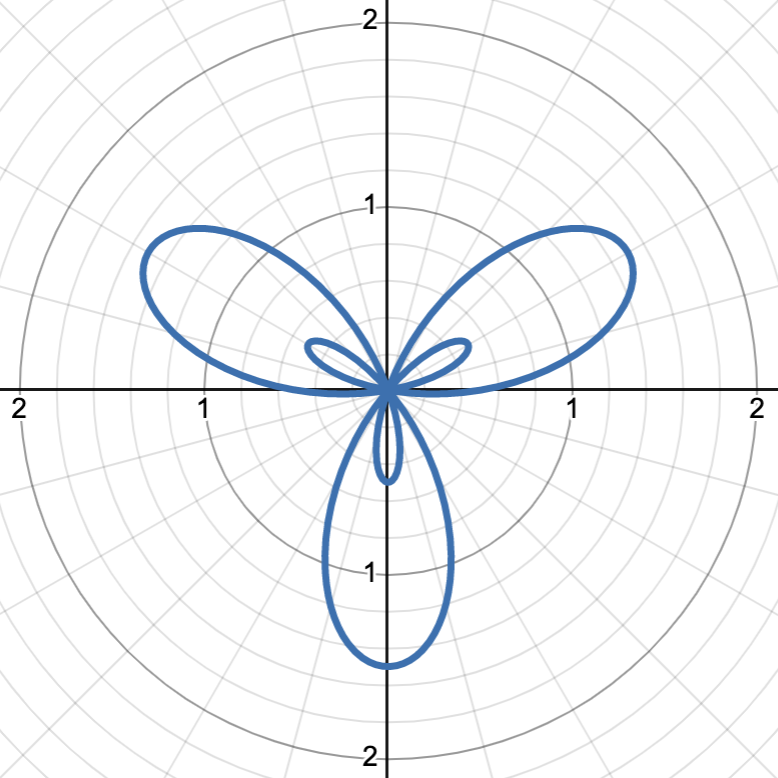
19
New cards
r = a + b sin(nθ) OR r = a + b cos(nθ), n is even positive integer > 1, b > a
rose curve with petals in between the main petals, amplitude of both petals determined by value of b - a (small petal) and b + a (big petal), 2n is the number of petals
graph shows r = 1/2 + cos(4θ)
graph shows r = 1/2 + cos(4θ)
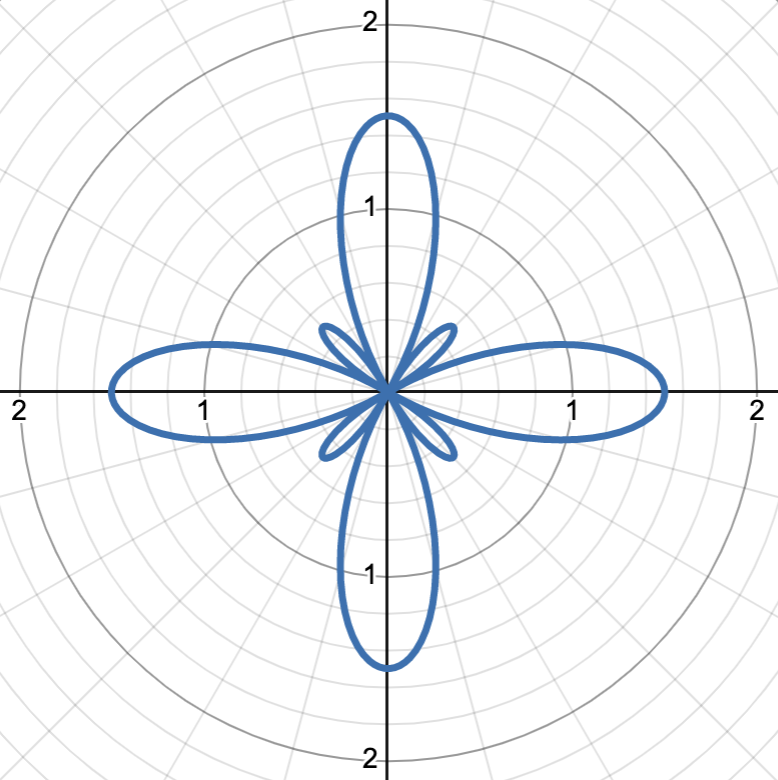
20
New cards
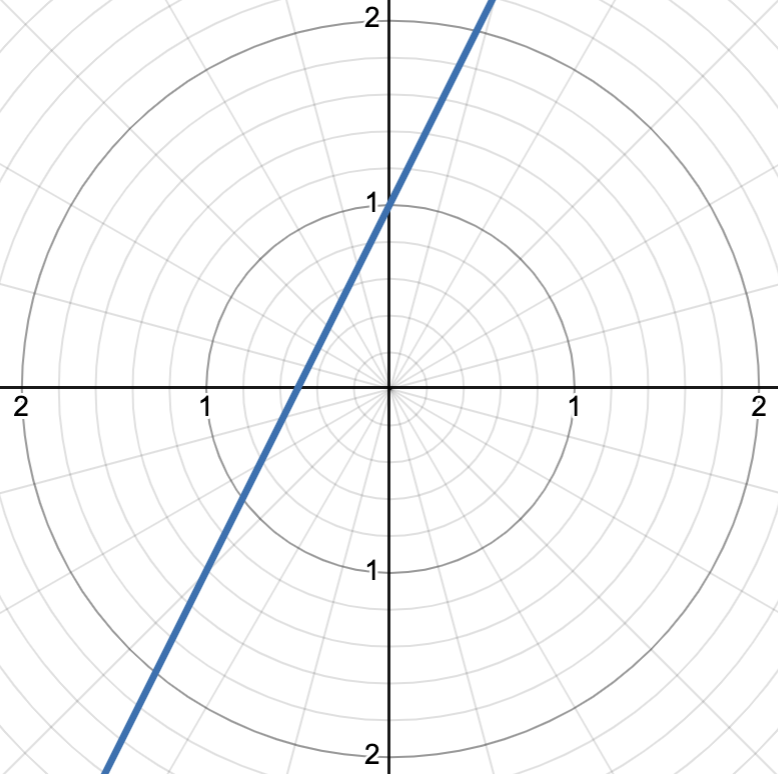
r = b/(sinθ - m cosθ)
straight line for the equation y = mx + b, where m and b are equivalent numbers
graph shows r = 1/(sin θ - 2 cos θ), or y = 2x + 1
graph shows r = 1/(sin θ - 2 cos θ), or y = 2x + 1