Moving Charges & Magnetism (copy)

Lorentz force

Force experienced by a charged

Biot Savart’s Law

Magnitude of the magnetic field due to a small current carrying element is

• directly proportional the current I

• directly proportional the length element

• inversely proportional to square of the distance

|dB| = μ₀Idlsinθ/4πr²

μ₀/4π = 10⁻⁷ Tm/A

Magnetic Field due to a Circular loop

At axial line:

μ₀IR²/2(R²+x²)³/²

At the centre of the loop with N turns:

B = N(μ₀I/2R)

Magnetic Field due to a Circular Arc

B = (μ₀I/4πR) x θ

Ampere’s Circuital Law

Ampere’s law states that the integral of magnetic field over a loop is equal to μ₀ times the total current passing through the surface

∮ B . dl = μ₀I

It is used when:

• B is tangential

• B ≠0

• B is normal to the closed loops

Magnetic Field due to an Infinitely Long thin Current Carrying Wire

B = μ₀I/2πr

Magnetic Field due to an Infinitely Long Thick Current Carrying Wire

B (in) = (μ₀I/2πR²) x r

B (surface) = μ₀I/2πR

B (outside) = μ₀I/2πr

R => Radius of circle

r => Distance between centre and point P

Magnetic Field due to a Finite Current Carrying Wire

B = μ₀I/4πR(sinΦ₁+ sinΦ₂)

Magnetic Field due to a Solenoid

nμ₀I

n = N/l (turns per unit length)

Magnetic Force

F = q (v × B) = Bqvsinθ n^

[B] = [F/qv]

S.I. unit: Tesla (T)

• Tesla is a rather large unit

• Smaller unit: Gauss

1 gauss = 10^-4 T

It is zero if:

• Charge moves parallel or anti-parallel

• Charge is at rest

• Particle is neutral

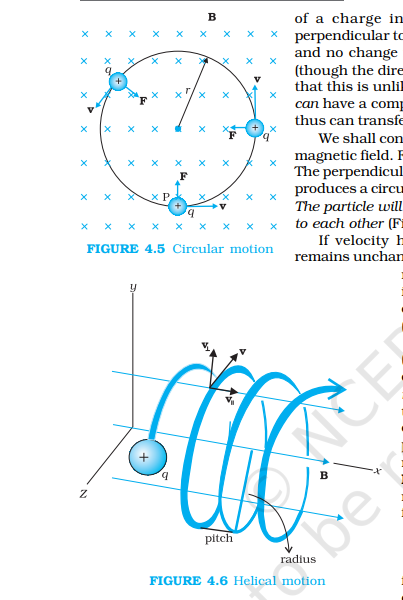
Motion of a Charge in Magnetic Field

r = mvsinθ/Bq

T = 2πm/Bq

f = Bq/2πm (1/T)

ω = Bq/m

pitch, x = v (parallel) x T = Vcosθ x 2πm/Bq

Path of Charge:

• Straight Line (θ = 0°)

• Circular Path (θ = 90°)

• Helical Path (θ ≠ 0°/90°/180°)

Magnetic Force on a Current Carrying Conductor

F = I(current) (l(length vector) x B)

F = BIlsinθ (remember as billsinθ)

l => length vector, the same direction as the current

B => External magnetic field, not the field produced by the rod

Force Between Parallel Two Current Carrying Wires

F/l = μ₀I₁I₂/2πd

Current in the same direction => Attract

Current in different directions => Repel

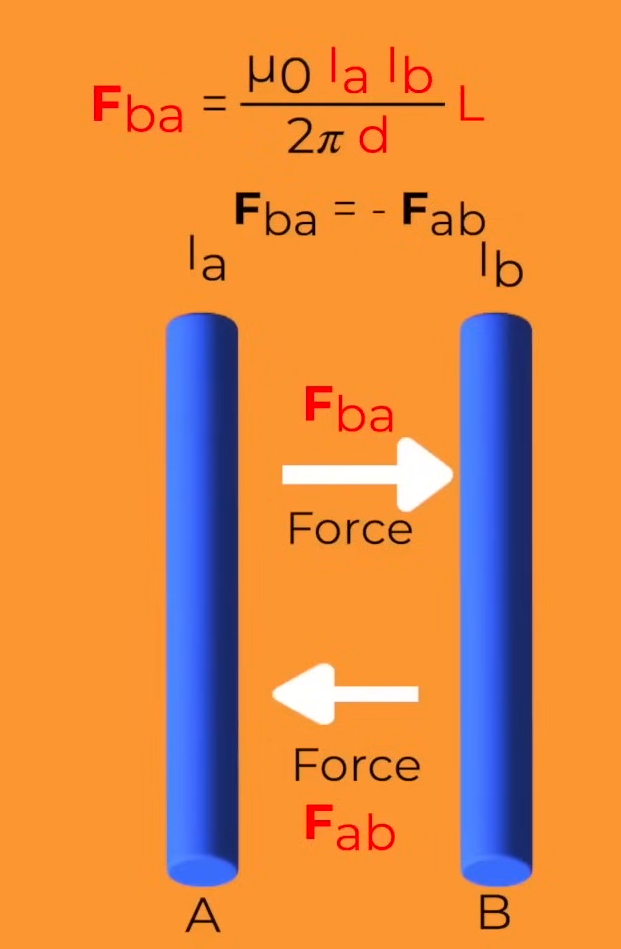
1 Ampere

1A is the current passing through 2 parallel wires which are separated by 1m and they experience a force of 2×10⁻⁷ N/m

Magnetic Dipole Moment

m = NIA

Torque Acting On A Current Carrying Loop In A Magnetic Field

𝜏 = IAB

𝜏 = IABsinθ

𝜏 = mbsinθ

Circular Current Loop As A Magnetic Dipole

(μ₀/4π)(2m/x³)

Moving Coil Galvanometer

Device used to measure small currents/detect current flow

Φ (deflection) ∝ I (current flowing)

Current Sensitivity (Iₛ)

Deflection per unit current

Iₛ = Φ/I = NBA/K

Voltage Sensitivity (Vₛ)

Deflection per unit voltmeter

Vₛ = Φ/V = NBA/KRg

Figure of Merit (K)

Current required to create unit deflections

K = I/Φ = K/NBA

Galvanometer to Ammeter

By adding a shunt resistance in parallel

Rₛ = (Ig/I-Ig) Rg

Rₛ => Required shunt resistance

I => Total current to be measured

Ig => Current flowing through galvanometer

I-Ig => Remaining current flowing through resistor

Total resistance of ammeter:

Rₐ = Rg x Rₛ/Rg+Rₛ (since they are parallel)

Galvanometer to Voltmeter

By adding a resistance in series

V = Ig(R+Rg)

R = V/Ig - Rg

R => Unknown resistance to be measures

Rg => Resistance of galvanometer

Rᵥ = R + Rg