Signifikanztests I (nach Fisher und Neyman & Pearson)

Weshalb schadet der p-Wert seit Jahren der Wissenschaft?

• viele Ergebnisse in Psychologie/Sozialwissenschaften nicht replizierbar

• p-Werte & Signifikanztests häufig falsch interpretiert

• Plausibilität von Forschungshypothesen wird im Signifikanztest nicht berücksichtigt

• Signifikanztestergebnisse werden ohne die Berücksichtigung von Effektstärken interpretiert

• Problem “p-hacking” in der Forschungspraxis

Beschreibe die 4 Schritte des Signifikanztests nach Fisher

1. Hypothese aufstellen, die widerlegt werden soll (H0)

2. Risiko festlegen, mit dem der Fehler 1. Art begangen werden soll

3. P-Wert berechnen (=Wahrscheinlichkeit, die Werte der vorliegenden Stichprobe oder noch extremere Werte zu erhalten, für den Fall, dass die H0 stimmt)

4. Ist der p-Wert kleiner als das alpha-Niveau?

   ja→lehne H0 ab

   nein→keine Schlussfolgerung möglich

Wie interpretiere ich ein signifikantes Ergebnis beim Signifkanztest nach Fisher?

Either an exceptionally rare chance has occurred, or the theory…is not true”

Wie interpretiere ich ein nicht signifikantes Ergebnis beim Signifikanztest nach Fisher?

daraus kann man nicht schließen, dass H0 zutrifft →denn es ist nichts über den Fehler bekannt, H0 fälschlicherweise zu akzeptieren → es lässt sich keine Aussage treffen

Was ist die Alternativhypothese, was ist die Nullhypothese?

Alternativhypothese (H1): formuliert die (operationalisierte) Forschungshypothese

Nullhypothese (H0): komplementär zur Alternativhypothese

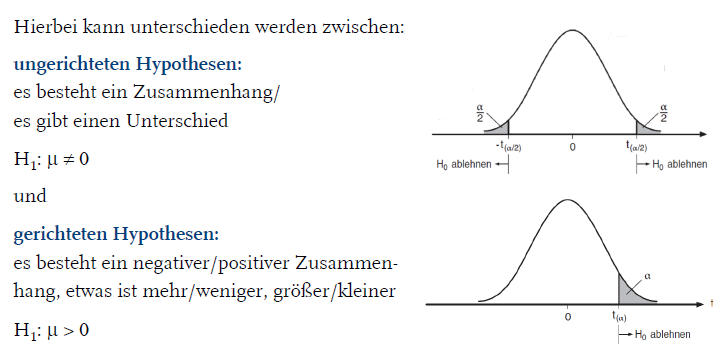
Was sind ungerichtete Hypothesen, was gerichtete Hypothesen?

ungerichtet: es besteht ein Zusammenhang/es gibt einen Unterschied

H1: μ ≠ 0

gerichtet: es besteht ein negativer/positiver Zusammenhang, etwas ist mehr/weniger, größer/kleiner →gerichtete Hypothesen sind informationsreicher

H1: μ > 0

Was sind unspezifische Hypothesen, was spezifische Hypothesen?

unspezifische Hypothesen: keine Größe des Zusammenhangs angegeben

H1: μ > 0

spezifische Hypothese: Größe des Zusammenhangs genannt →spezifische Alternativhypothesen sind informationsreicher

H1: μ > 0,3

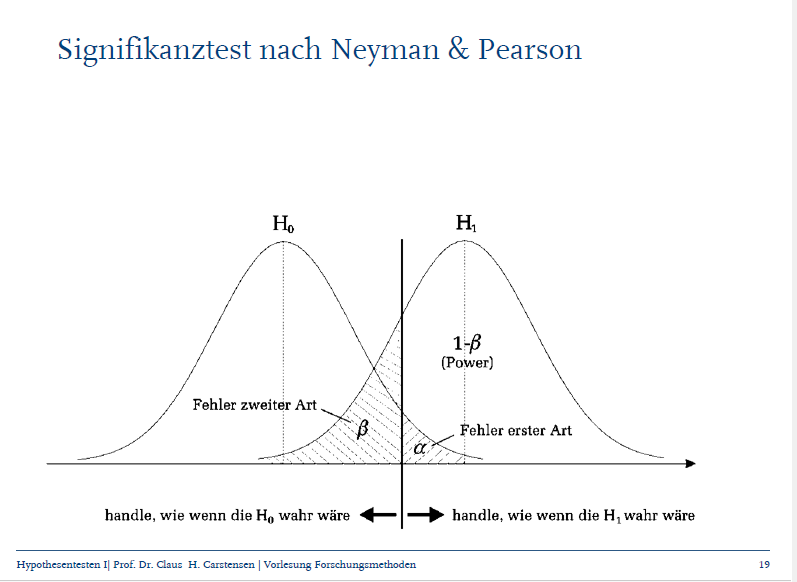
Erkläre den Unterschied zwischen dem Fehler 1. Art und dem Fehler 2. Art

• aufgrund der Daten wird sich für H0 entschieden, H0 gilt in der Population (1-alpha →Sicherheitswahrscheinlichkeit)

• aufgrund der Daten wird sich für die H1 entscheiden, H0 gilt in der Population (alpha) = Fehler 1. Art

• aufgrund der Daten wird sich für H0 entschieden, H1 gilt in der Population (beta) = Fehler 2. Art

• aufgrund der Daten wird sich für H1 entscheiden, H1 gilt in der Population (1-beta) = Teststärke/Power

Erkläre die 4 Schritte eines Signifikanztests nach Neyman & Pearson

1. Hypothese aufstellen, die widerlegt werden soll (H0)

2. Komplementäre Alternativhypothese aufstellen

3. Risiken für Fehler 1. Art und Fehler 2. Art festlegen (Effektstärke? Sensitivität und Spezifität? Stichprobengröße?)

4. p-Wert berechnen: Wahrscheinlichkeit, die Prüfgröße der vorliegenden Stichprobe oder noch extremere Werte zu erhalten, für den Fall, dass die H0 stimmt

   →wenn der p-Wert kleiner/gleich dem spezifizierten alpha ist, verhalte dich, als wäre die H1 richtig

   →wenn der p-Wert größer als das spezifizierte alpha ist, verhalte dich, als wäre die H0 richtig

Welche Aussagen lassen sich nun beim Signifikanztest von Neymann & Pearson treffen (im Vgl. zu Fisher)?

Neymann & Pearson geben eine Handlungsanweisung, was zu tun ist, wenn p-Wert kleiner oder größer als das spezifizierte alpha ist

Und wie kann festgestellt werden, ob der statistische Test überhaupt inhaltlich bedeutsam ist?

mit der Effektstärke (=standardisiertes Maß für die gesuchte Stichprobenstatistik, z.B. Cohen’s d für Mittelwertsunterschiede oder erklärte Varianz in der ANOVA)

In der Praxis werden oft keine Powerberechnungen durchgeführt, und es finden keine theoretischen Überlegungen statt zum Risiko mit dem man den Fehler 1./2. Art begehen möchte. Welche Chancen werden hierdurch vergeben?

• zu erkennen, ob die Power des Tests zu gering war

• Spezifitäts- und Sensitivitätsüberlegungen für die praktische Relevanz von Aussagen

• Inhaltliche Bedeutsamkeit der Ergebnisse zu überprüfen

• Optimale Stichprobengrößen

Wovon hängt Teststärke ab?

1. Signifikanzniveau (α):

   • Höheres α → geringere β-Fehlerwahrscheinlichkeit → höhere Teststärke.

   • Nachteil: mehr falsch-positive Ergebnisse.

2. Effektstärke (z. B. Cohen’s d):

   • Größere Effekte sind leichter nachweisbar → höhere Teststärke.

3. Stichprobengröße (n):

   • Größeres n → kleinere Standardfehler → Unterschiede werden eher signifikant.

👉 Merksatz: Power ↑ bei größerem α, stärkerem Effekt, größerem n.

Welche Arten von Poweranalysen gibt es und was wird jeweils berechnet?

1. A-priori-Poweranalyse

   • Gegeben: α, gewünschte Power (1−β), Effektgröße

   • → Berechnet: benötigte Stichprobengröße (n)

2. Post-hoc-Poweranalyse

   • Gegeben: α, n, Effektgröße

   • → Berechnet: tatsächliche Power (1−β)

3. Kriteriums-Poweranalyse

   • Gegeben: β, n, Effektgröße

   • → Berechnet: notwendiges α

4. Sensitivitätsanalyse

   • Gegeben: α, β, n

   • → Berechnet: Effektgröße, die mit dieser Stichprobe noch nachweisbar ist

5. Kompromissanalyse

   • Gegeben: Verhältnis α/β, n, Effektgröße

   • → Berechnet: passende α- und β-Werte

👉 Merksatz:

• A priori → „Wie viele brauche ich?“

• Post hoc → „Wie stark war mein Test wirklich?“

• Kriterium → „Welches α wäre nötig?“

• Sensitivität → „Welche Effekte kann ich überhaupt sehen?“

• Kompromiss → „Wie balanciere ich α und β?“

Was ist Sensitivität und wie berechne ich sie?

→Fähigkeit eines Testes, die tatsächlich Betroffenen richtig zu identifizieren

→Sensitivität = richtig positiv / (richtig positiv + falsch negativ)

Was ist Spezifität und wie berechne ich sie?

→Fähigkeit eines Testes, die nicht Betroffenen richtig zu identifizieren

→Spezifität = richtig negativ / (richtig negativ + falsch positiv)

Wie lässt sich Sensitivität und Spezifität auf statistische Tests übertragen?

→genau wie Sensitivität und Spezifität verhalten sich der Fehler 1. und 2. Art zueinander

Statistischer Test kann entweder:

• hohes Risiko eingehen, einen Fehler 1. Art zu begehen (→Wahl eines hohen Alphaniveaus)

• hohes Risiko eingehen, einen Fehler 2. Art zu begehen (→Wahl eines niedrigen Alphaniveaus)

• Kompromiss eingehen (→Wahl eines mittleren Alphaniveaus)

Die Festlegung des alpha- und beta-Fehlerniveaus kann als eine Risiko-Nutzen Abwägung betrachtet werden. Wieso wird oft trotzdem mit einem “pauschalen” Fehlerniveau von alpha=5%, Teststärke von 80% (beta Fehler von 20%) getestet?

Weil in der Forschungspraxis viele Fragen keine gesellschaftliche Relevanz haben

Warum ist eine zu kleine oder auch eine zu große Stichprobe problematisch?

zu klein: zu niedrige Teststärke, auch bedeutsame Effekte werden nicht signifikant

zu groß: auch unbedeutende Effekte werden statistisch signifikant

Wie finde ich meine optimale Stichprobengröße

→hierfür müssen Informationen über die Größe des erwarteten Effekts vorliegen

• Literaturrecherche

• theoretische Implikationen aufgrund praktischer Relevanz (wann ist mir der Effekt noch groß genug)

Wieso wird die Power manchmal auch erst post-hoc berechnet?

• Nutzung vorhandener Daten

• keine Kenntnis über erwarteten Effekt

• nur bestimmte Anzahl an Versuchspersonen ist rekrutierbar

Was kann aus einer Powerberechnung resultieren?

• zu kleine Stichprobe gezogen (sehr niedrige Teststärke)

  →Replikation mit ausreichend großer Stichprobe

• zu große Stichprobe gezogen (sehr hohe Teststärke)

  →Berichten und Interpretieren Effektgrößen, Testen an spezifischerer Hypothese

Lernkontrollfrage 1: Wovon hängt die Teststärke ab?

• Signifikanzniveau

• Effektstärke

• Stichprobengröße

Lernkontrollfrage 2: entwickeln Sie ein Beispiel, welches die Relevanz der Risiko-Nutzen-Abwägung beim Signifikanztest zeigt

Beispiel: Medikamententest

• H₀: Medikament wirkt nicht.

• H₁: Medikament wirkt.

👉 Risiko (α-Fehler): Wir glauben, das Medikament wirkt (Ablehnung von H₀), obwohl es in Wahrheit wirkungslos ist → Patienten bekommen nutzloses Medikament, evtl. Nebenwirkungen.

👉 Nutzen (geringer β-Fehler / hohe Teststärke): Wir erkennen rechtzeitig, wenn das Medikament tatsächlich wirkt → Behandlung verbessert Leben.

Abwägung:

• In der Medizin wählt man oft ein sehr kleines α (z. B. 0,01), um falsch-positive Befunde zu vermeiden.

• Aber: zu streng gewählt → mehr β-Fehler (echte Wirkungen werden übersehen).

Merksatz:

• Niedriges α schützt vor falschem Alarm.

• Hohes Power (1−β) schützt vor übersehenen Effekten.

• Optimales α hängt von den Folgen des Fehlers ab.