Chapter 18 simple harmonic motion

What is said to be oscillating

Anything that vibrates back and forth about a midpoint

For an oscillating object what is the midpoint

The equilibrium position

What happens to the displacement of an object as it oscillates

Constantly changes with respect to the equilibrium position

Amplitude definition

Maximum displacement of the oscillating object from equilibrium

Free vibrations definition

If amplitude is constant and no frictional forces are present oscillations are described as free vibrations

Time period definition

T, of the oscillating motion is the time for one complete cycle (T=1/f)

frequency definition

Number of cycles per second made by an oscillating object. Hz

Angular frequency definition

2π/T = 2πf unit → rads-^1

What is phase difference

Tells us how two oscillating objects with the same speed are moving with respect to each other

For two objects oscillating at the same frequency what is their phase difference

2πΔt/T (radians)

Examples of SHM

Pendulums And mass on a spring

Simple harmonic motion definition

Oscillating motion in which the acceleration is proportional to displacement and always in the opposite direction to displacement

What is a fiducial mark

The point where you measure an oscillation from

Why is the middle used for a fiducial mark

Point where the object is moving the fastest so should give the smallest uncertainty

Equations for mass on a spring

T= 2π√m/k

Force = kΔl

Springs in parallel

Spring constant= kp + kq

Springs in series

1/k = 1/kp +1/kq

Equation for a pendulum

T = 2π√l/g

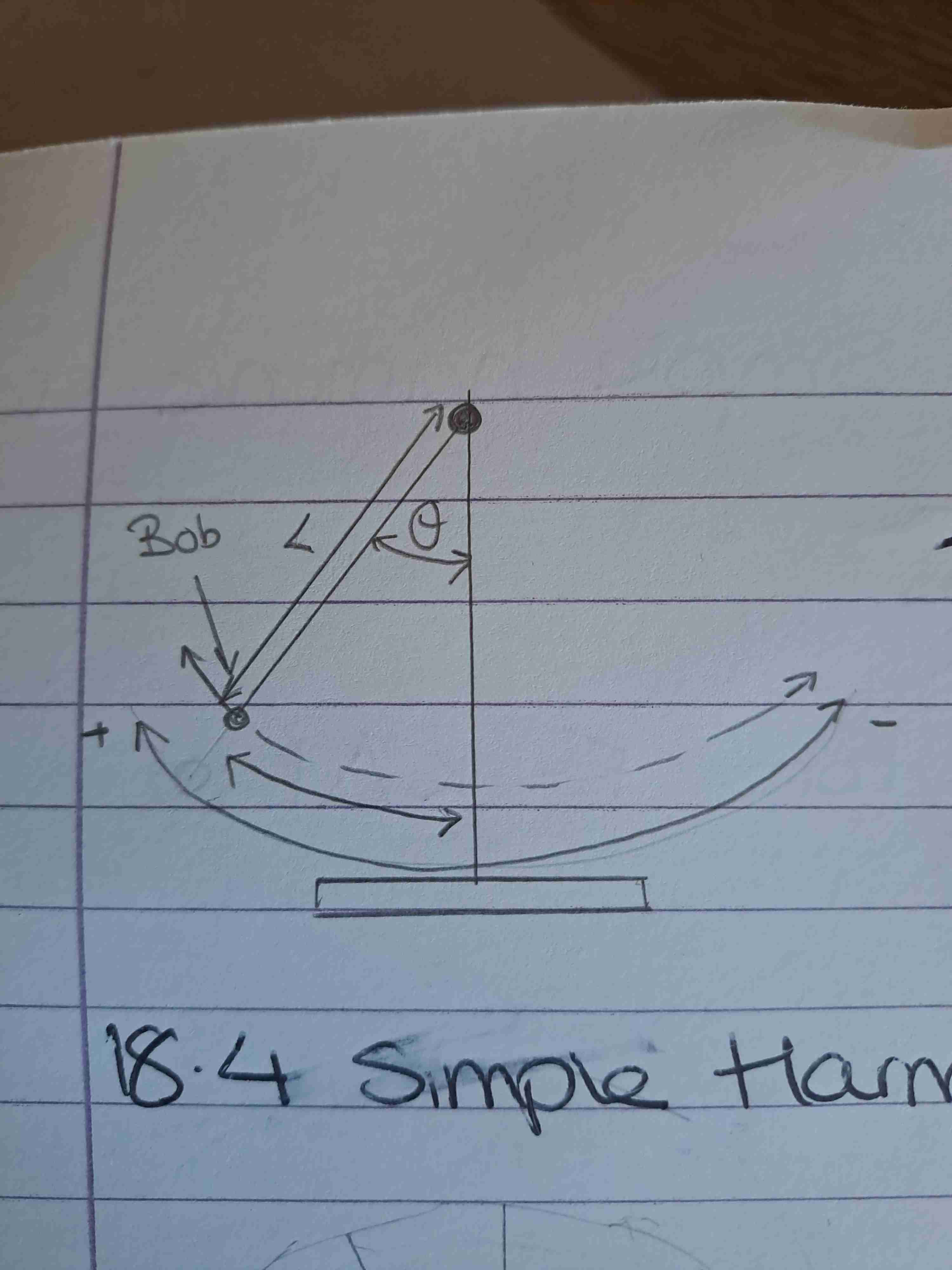
What is simple harmonic motion linked with

Circular motion

What happens to the amplitude in free oscillations

Is there is no friction the amplitude will not decrease

What happens to energy in free oscillations

Energy changes from potential to kinetic energy constantly

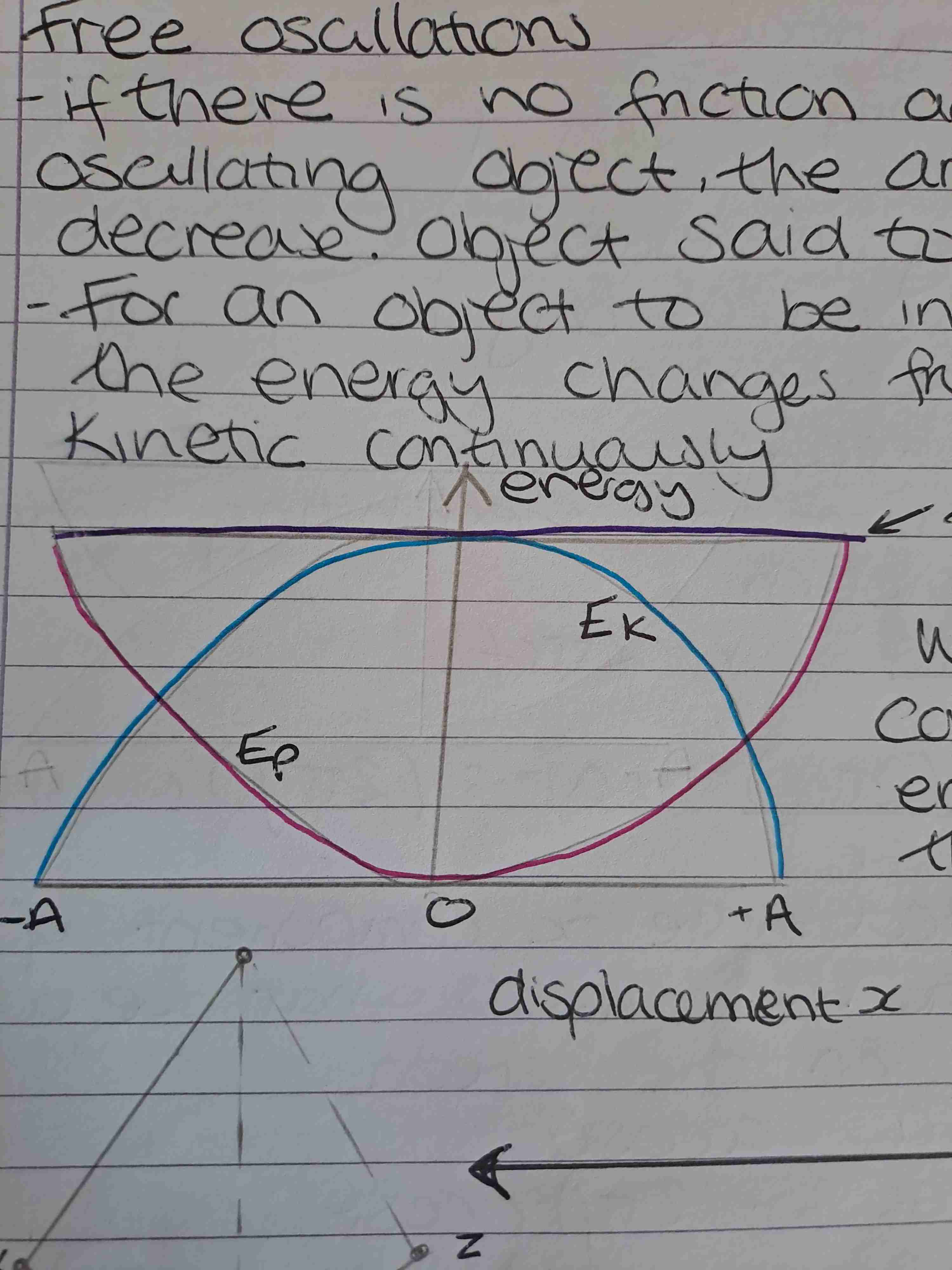
What does Etotal equal

Potential energy + kinetic energy

When a pendulum is at the midpoint what is the kinetic and potential energy

Potential energy=0

Kinetic energy= Etotal

When a pendulum is at the maximum amplitude what is the kinetic and potential energy

Potential energy = Etotal

Kinetic energy= 0

What is x

Displacement

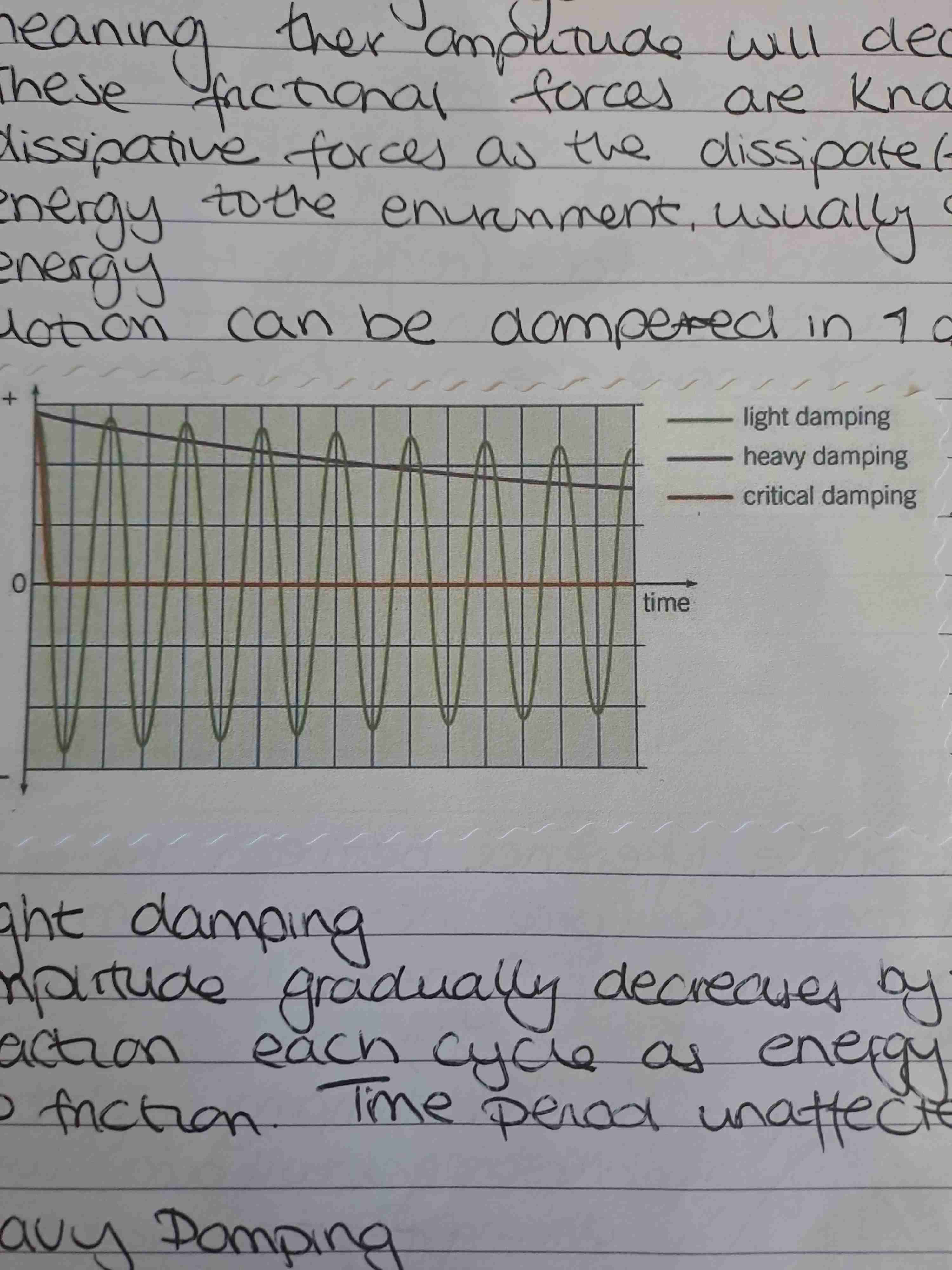
How can motion be dampened

Light, heavy and critical damping

What is light damping

Amplitude gradually decreases by the same fraction each cycle as energy lost due to friction. Time period unaffected

What is heavy damping

Friction so great no oscillations occur. The displaced object slowly returns to equilibrium

What is critical damping

Friction just enough to stop the system oscillating after it has been displaced from equilibrium. system returns to equilibrium in the shortest possible time without over shooting the equilibrium position

What type of damping do car suspension systems use

Critically damped

Damping graph

Graph

What is natural frequency

All objects have a frequency they will vibrate at known as their natural frequency

When will a system vibrate at its natural frequency

When a system vibrates without a driving force

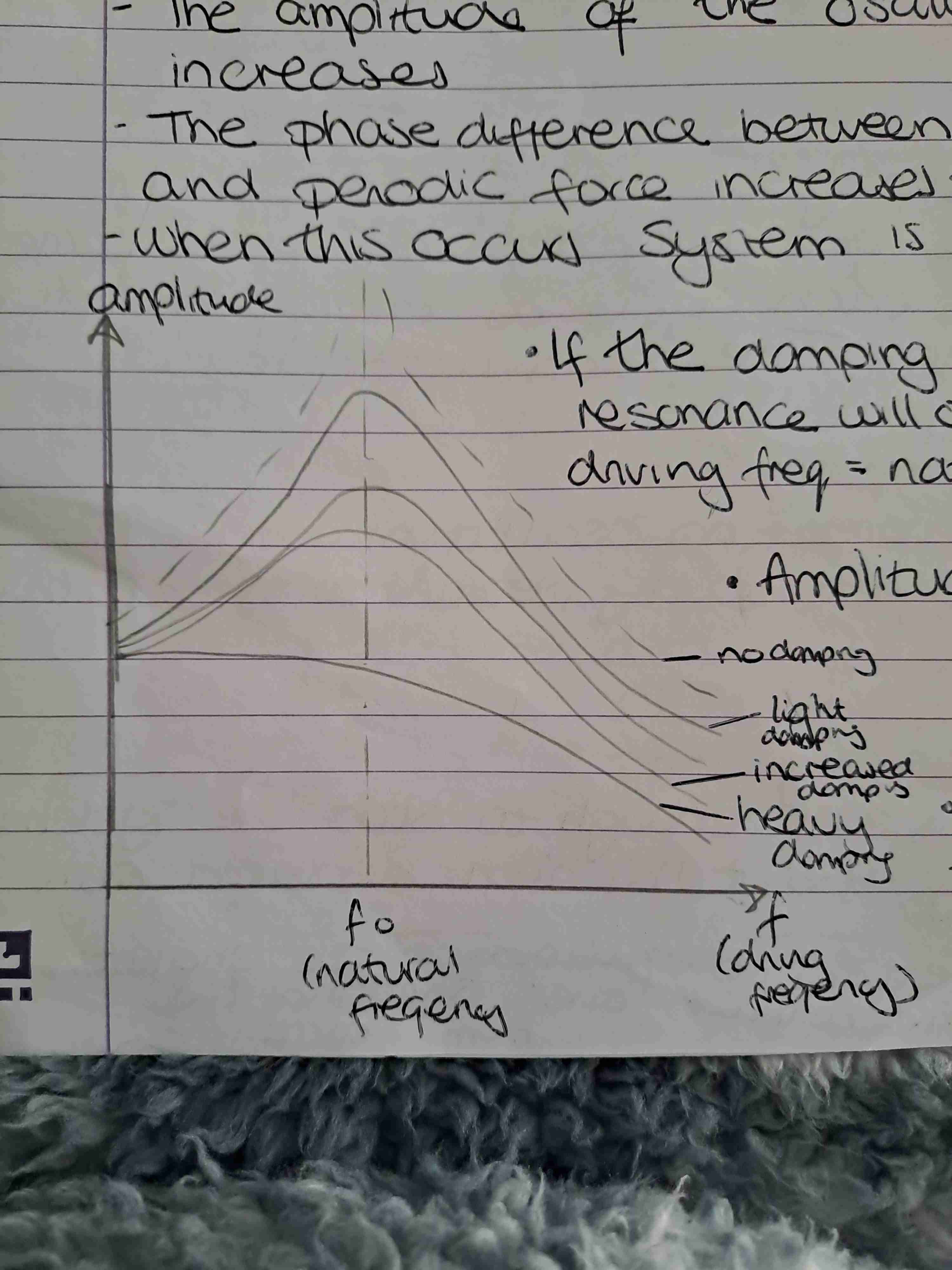
What happens when a periodic force is applied to a system

The system will undergo forced oscillations

What happens if the periodic force is below or above the natural frequency

The system will exhibit small amplitude oscillations at the same frequency as the driver

What happens if the frequency of the driver matches the systems natural frequency

The amplitude of the oscillations dramatically increases

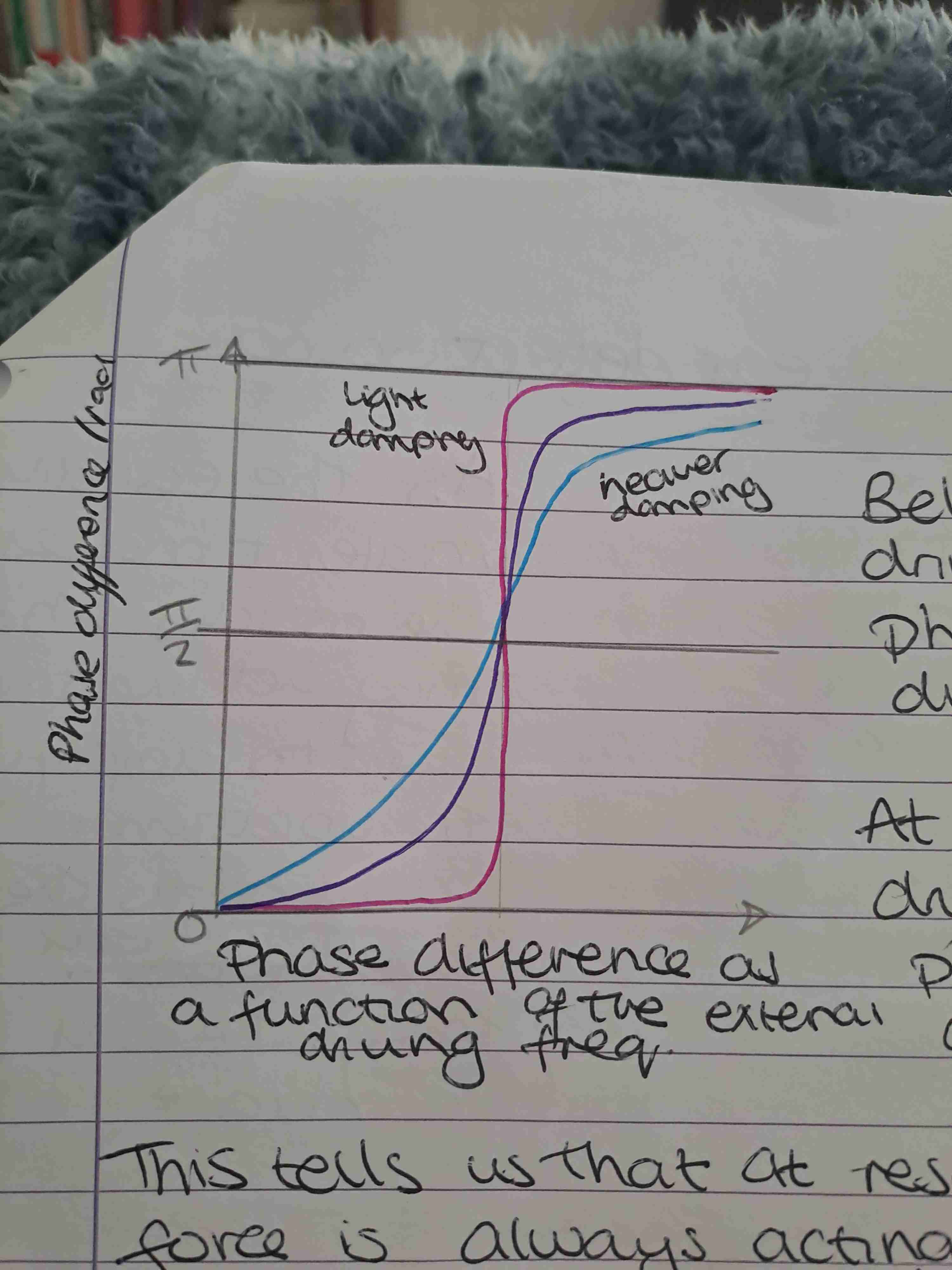
the phase difference between the displacement and periodic force increases from 0 to π/2

When this occurs the system is in resonance

If damping is light when will resonance occur

When the driving frequency equals natural frequency

What is amplitude during resonance limited by

Damping

(Heavier damping=further from natural frequency max A occurs)

Natural frequency graph

Graph

When is the driving frequency in phase with the displacement of the system

Below resonance

At resonance what is the phase difference between the driving frequency and the displacement of the system

π/2 out of phase

At resonance where does the driving force always act

At the same point in each cycle causing the amplitude to increase

Above resonance what is the phase difference between the driving frequency and the displacement of the system

π out of phase

What are the dangers of resonance and how can you remove the dangerous effects

Resonance can have dangerous effects for structures especially bridges

To avoid make structure stiffer add dampeners and change the mass

Graph of phase difference as function of the external driving frequency

Graph

What is the velocity time graph the gradient of

The displacement time graph

What is the acceleration graph the gradient of

The velocity time graph

What is the phase difference of the velocity time graph and displacement time graph

π/2

Displacement velocity acceleration time graphs

Graph

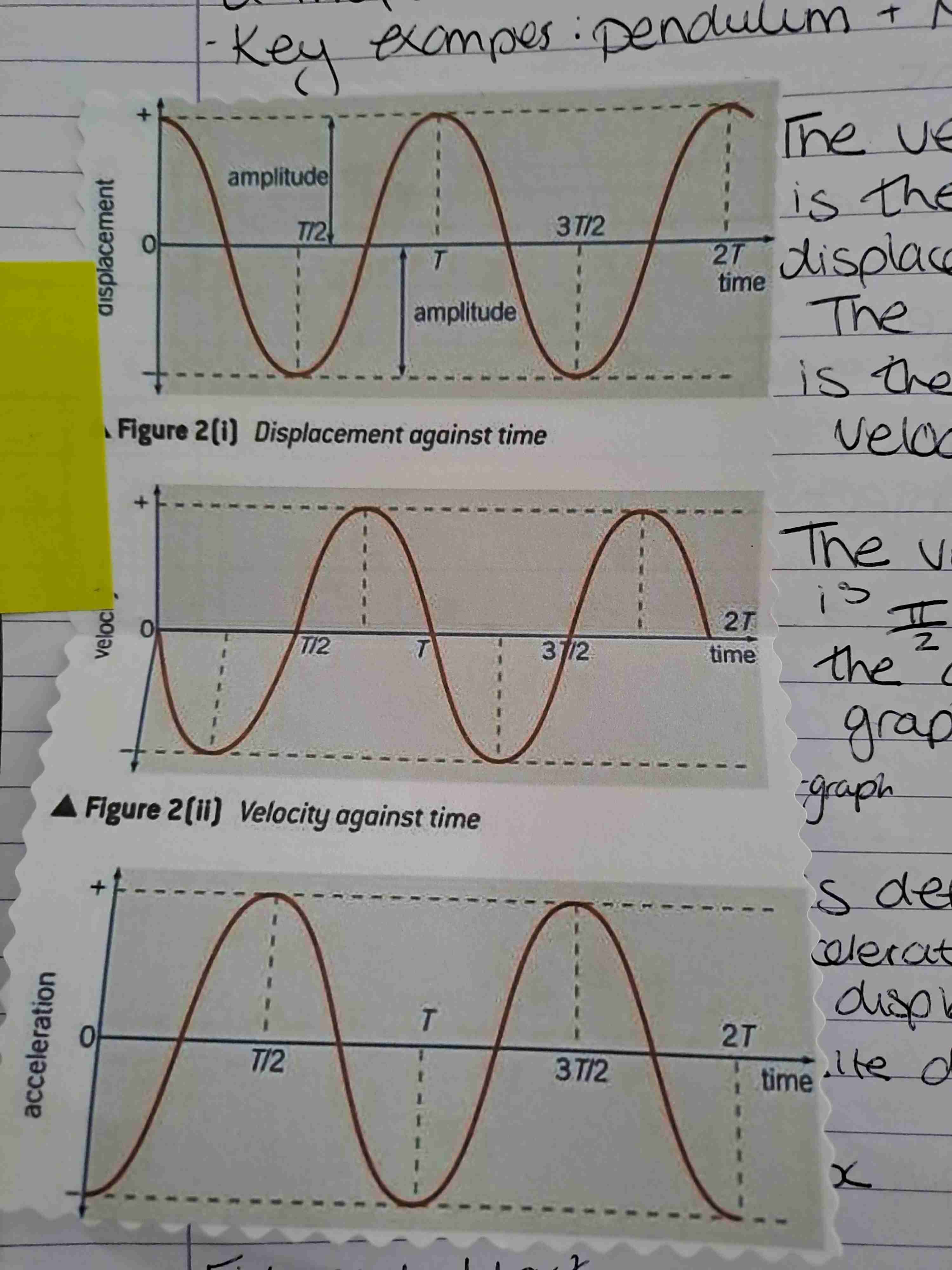
What's the phase difference of the acceleration time graph and displacement time graph

π out of phase

What is x as a trig function of t and w

x=Acos (2πft)

X=Asin(wt)

What is WT measured in

radians

Equation derivative of energies?

Equations