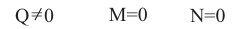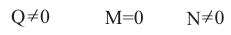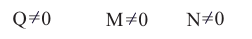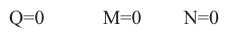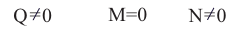momentane Bewegungszustände

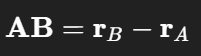
• Der Rotationsanteil ist immer senkrecht zu AB

• Alle Geschwindigkeiten unterscheiden sich nur durch ω×AB

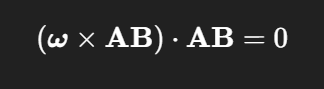
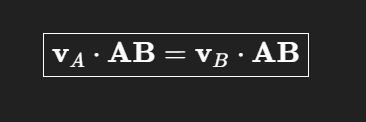
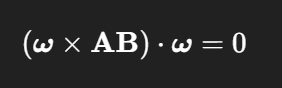
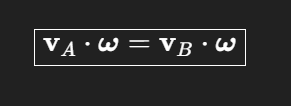
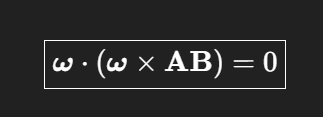
Immer null, niemals ungleich null

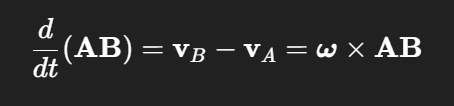
• AB ist NICHT null

• Aber Länge von AB bleibt konstant

• Nur die Richtung ändert sich (Rotation)

Momentane reine Translation

ω=0

• Translation entlang ω

• Rotation um ω

Schraubung

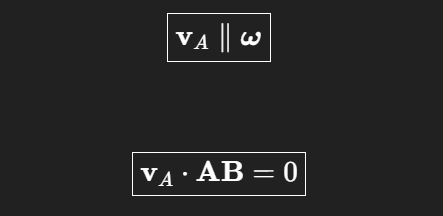
Auf der Zentralachse gilt:

• Geschwindigkeit ist parallel zu ω

• Keine Querbewegung

MO​=∑(ri​−rO​)×Fi​

Gesamtmoment um Punkt O

Schraubung (Zentralchse existiert immer)

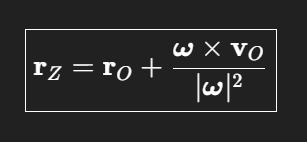
Lage der Zentralachse

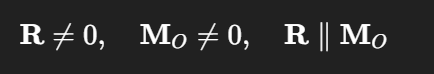
R * M ≠ 0

Schraubung

Mz = 0

R ≠ 0

R * M = 0

reine Translation

R = 0

M ≠ 0

R * M = 0

reine Rotation

R || w

Schraubung

Kräftegruppe kann nicht auf einen Punkt auf der Zentralachse reduziert werden

Moment von Punkt auf Zentralachse ist ungleich null (es müsste null sein)

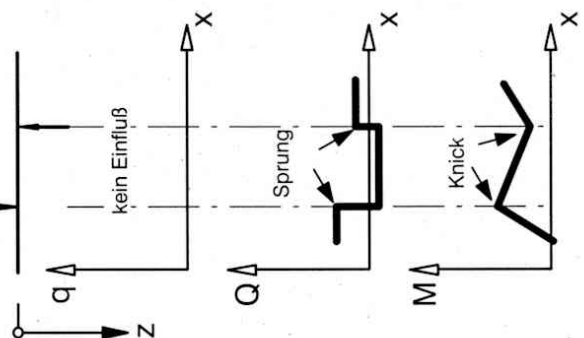
Einzelkraft

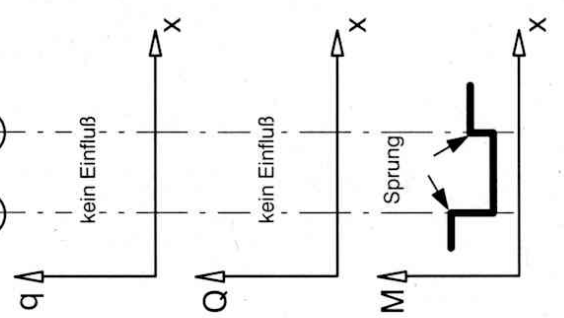
Einzelmoment

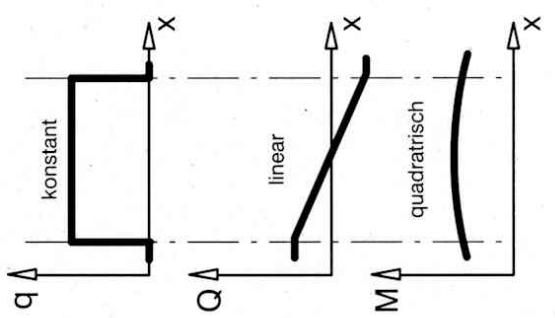
linienverteilte Kraft

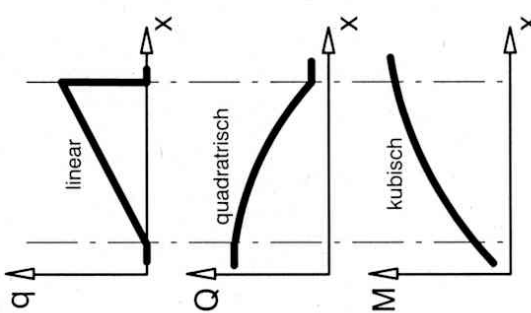
dreiecksverteilte Kraft

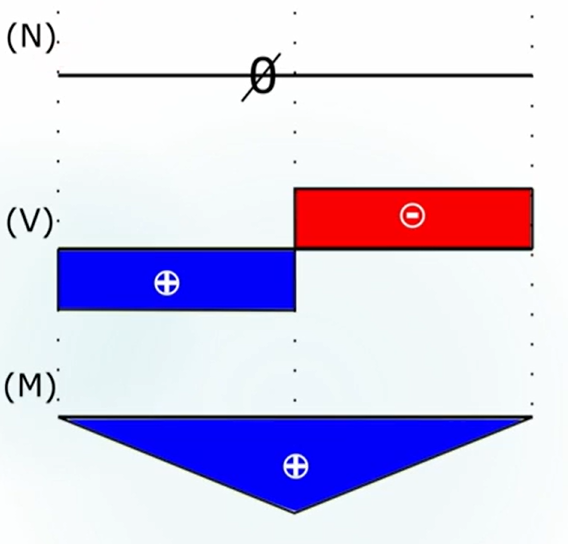
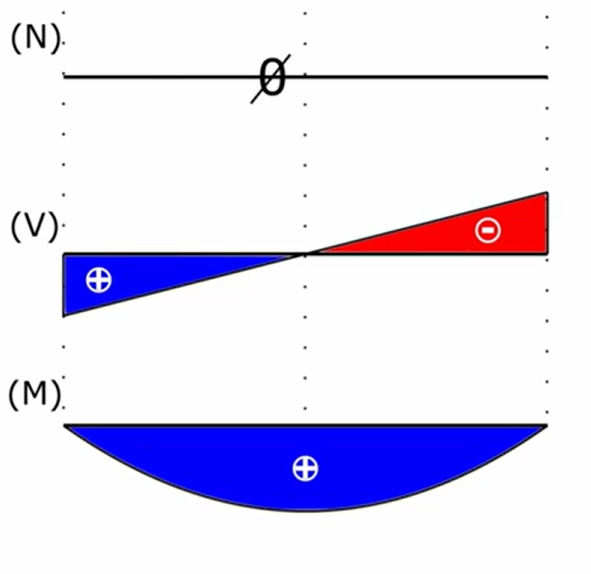
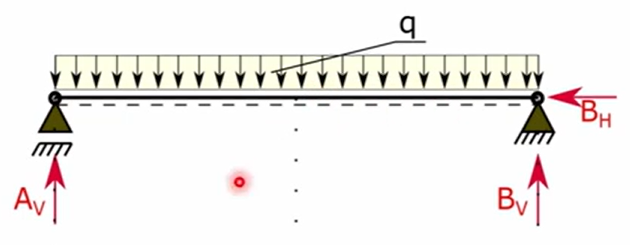
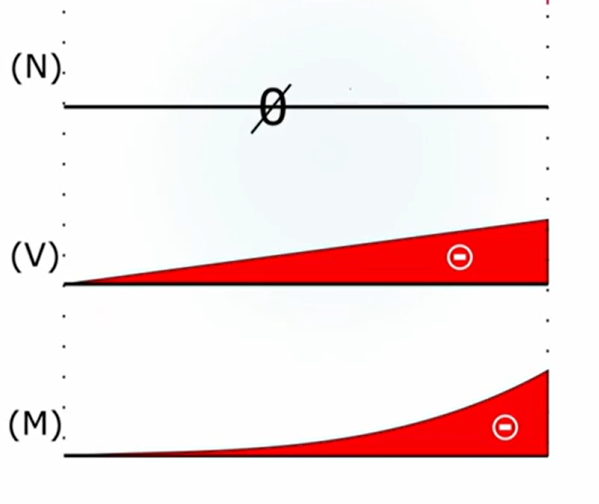
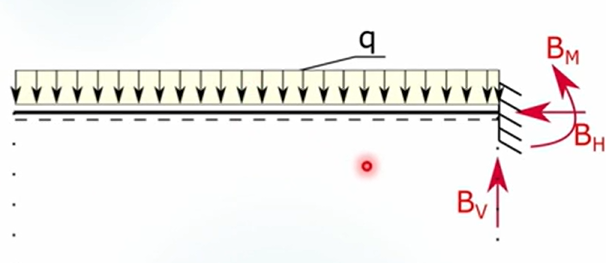
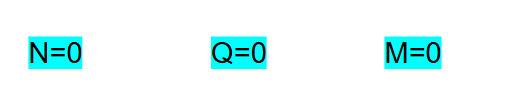
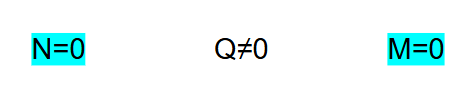
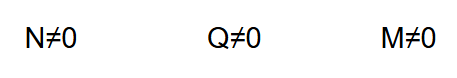
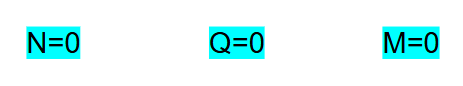
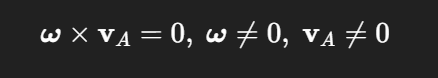
keine Garantie für momentane Rotation (kann auch Schraubung sein)

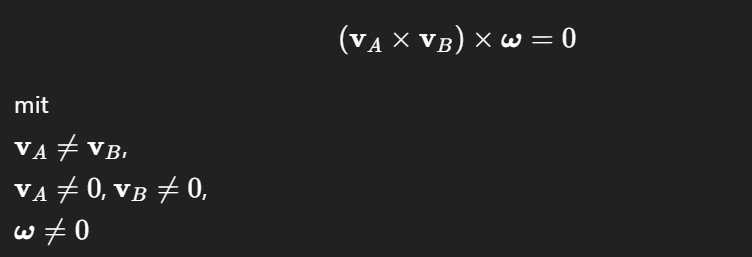
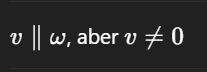
momentane Rotation

Relativgeschwindigkeit steht immer senkrecht auf AB

gilt für alle momentanen Bewegungszuständen (ausser reine Translation weil delta v = 0)

Schraubung

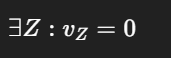
Momentane Rotation

Resultierende Kraft = 0 —> keine Einzelkraft

geschlossene Schleife von Kräften

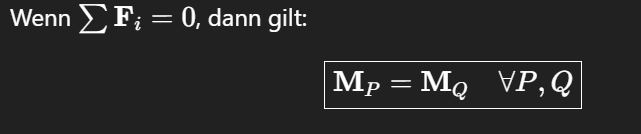
moment ist ortsunabhängig (reiens Moment - Kräftepaar)

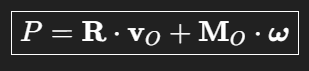
R = 0

—> P = M * w

Gesamtleistung bei Schraubung

M senkrecht auf Zentralachse

Leistung ist 0

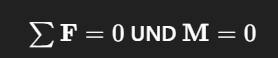
Gleichgewicht

S=(sum of A * rs) / (sum of A)

Schwerpunt

erste Invariante = 0

zweite Invariante = 0

Translation/Stilstand

erste Invariante ≠ 0

zweite Invariante = 0

Rotation

erste Invariante ≠ 0

zweite Invariante ≠ 0

Schraubung

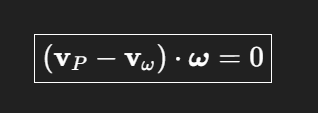
gilt für alle momentanten Bewegungszuständen (Rotation und Schraubung)

• Alle Punkte haben die gleiche Geschwindigkeitskomponente entlang ω

• Unterschiede in v sind immer quer zu ω

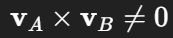
keine Translation

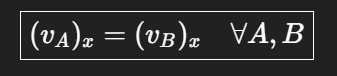
unabhängig wo Punkte A und B liegen

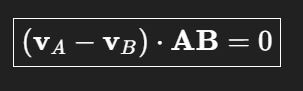
• gilt immer, sobald ω≠0\omega \neq 0ω=0

• nicht nur für reine Rotation!

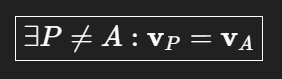
• auch möcglich wenn P nicht auf der Zentralachse liegt

• auch möglich wenn der Körper rotiert oder schraubt

• Geschwidnigkeitsfeld ist nicht injektiv

• Gleiche Parallelkomponente zu ω bei allen Punkte

• Relativgeschwindigkeit ⟂ Verbindungsvektor

• Gleiche Geschwindigkeiten ≠ gleiche Lage

• Translation ausgeschlossen, sobald vA×vB≠0

Merksätze

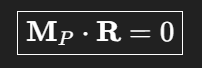
Kräftegruppe nur dann auf eine EInzelkraft reduzierbar

• Moment steht senkrecht zur Resultierenden

• keine Schraubung, kein Kräftepaar

• Moment unterschieden sich nur im Betrag, nicht Richtung (heisst Ma || Mb)

Gleichgewicht

statisch äquivalent (nicht Kräfte sind identisch)

Kräftegruppen haben gleiche virtuelle Leistung

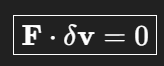
keine virtuelle Leistung (Kräfte parallel zur Rotationsachse)

virtuelle Rotation um Achse w

2 Kräftegruppen haben im beliebigen Punkt diesselbe Dyname

statisch äquivalent

R ≠ 0

zweite Invariante = 0

Einzelkraft

R = 0

Mp = 0

Nullsystem

R ≠ 0

zweite Invariante ≠ 0

Schraubung

R = 0

Mp ≠ 0

Kräftepaar (Moment)

R = 0

M = 0

Hauptsatz der Statik (Ruhelage des Systems)

• ist an beiden Enden gelenkig gelagert

• kann nur Kräfte in Stabrichtung aufnehmen —> nur Zug/ Druck (keine Querkräfte und Biegemomente)

• externe Kräfte greifen nur an Knotenpunkten an

Pendelstütze

Normalkraft wirkt innerhalb des Körpers

nicht kippen

N muss grösser als 0 sein (kein abheben)

Standfestigkeit