fundamentals of algorithm

what does this denote 

Denotes a set of elements

what does this symbol denote

empty set

what does this symbol denote 

variable or value is an element of a given set 

what does this symbol denote

variable or value is not a element of a given set

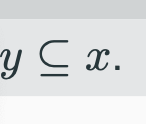
what does  this subset symbol denote 

variable is a subset of a given set 

what does  this subset symbol denote 

variable is a proper subset of a given set

what does (x,y) denote

a pair of values

what does this symbol denote |x|

size of a given set or list x

what does this symbol denote y[I]

ith element of a given list where I = 0,1, |y|-1

what does this symbol denote

floor value of a given value or variable

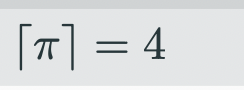
what does the ceiling symbol denote

ceiling value of a given variable or value 

what does mod or % denote

modulo

what is the definition of alphabet Σ

finite non empty set whose elements are called letters 

when is string y a factor of string x

when two strings exist

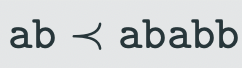
what is the Lexicographic order

strings induced by an order of letters and denoted by the same symbol

log(a) + log(b)

log(ab)

log(a) - log(b)

log(a/b)

log(n^k)

k log(n)

log(2^n)

n

2^log(n)

n

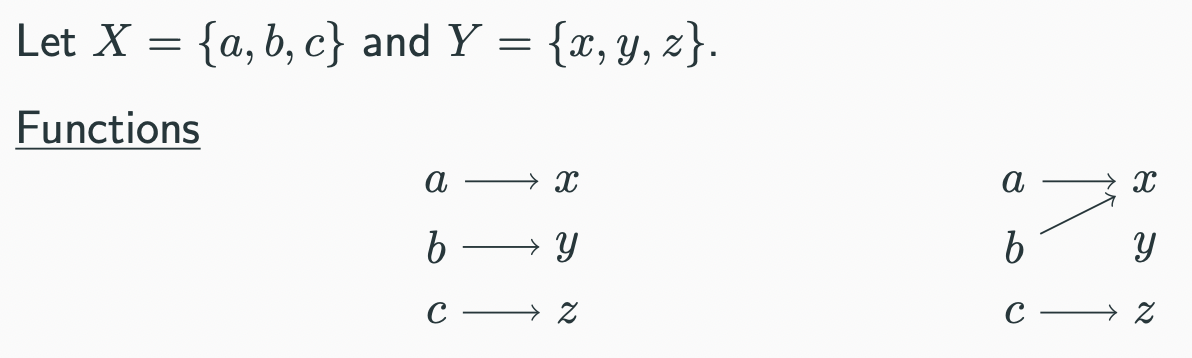
what does the function rule do

assigns each element of x to one element of y

what does space complexity change depend on

input and data structures used and size of output

what does pseudocode provide 

general description of the algorithm

input and output algorithm

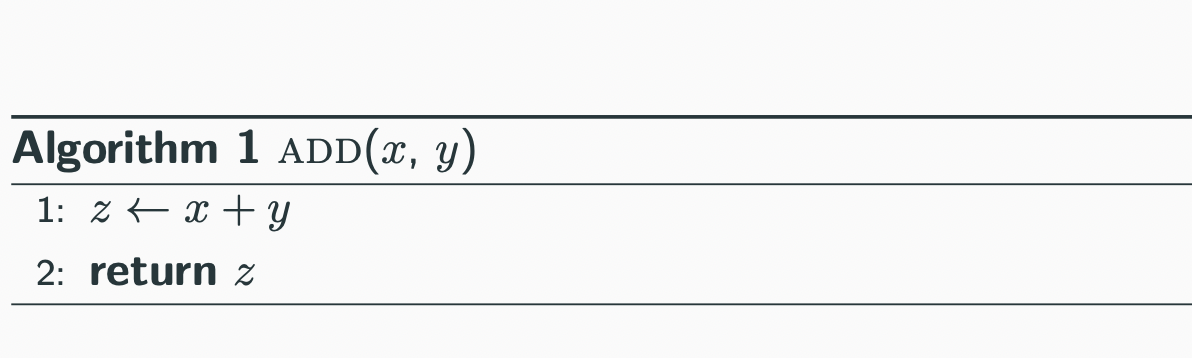
Assignment algorithm

if statement algorithm

for loop algorithm

while loop algorithm

what does Big O denote

the upper bound of the algorithm

what does big Ω (omega) denote

lower bound of the algorithm

what does big Θ denote

tight bound of an algorithm

O(1) Constant time

operation takes the same amount of time regardless of input size 

O(log(n)) Logarithmic time

time grows with logarithmically with input size

O(n) Linear time

Time grows proportionately to input size

O(n log(n)) Quasilinear time

Time grows slightly faster than linear 

O(n2) Quadratic time

time grows quadratically with input size  

O(n3) Cubic time

time grows cubically with input size

O(2n) Exponential time

Time grows exponentially with input size

what is a P (Polynomial) problem

time complexity can be expressed as O(n^k)

what is the NP (Non-deterministic Polynomial) problem

if a solution exist its correctness can be verified in polynomial time

when is a problem considered NP-Hard

NP problems can be reduced to its polynomial time

NP-Complete

both NP and NP hard

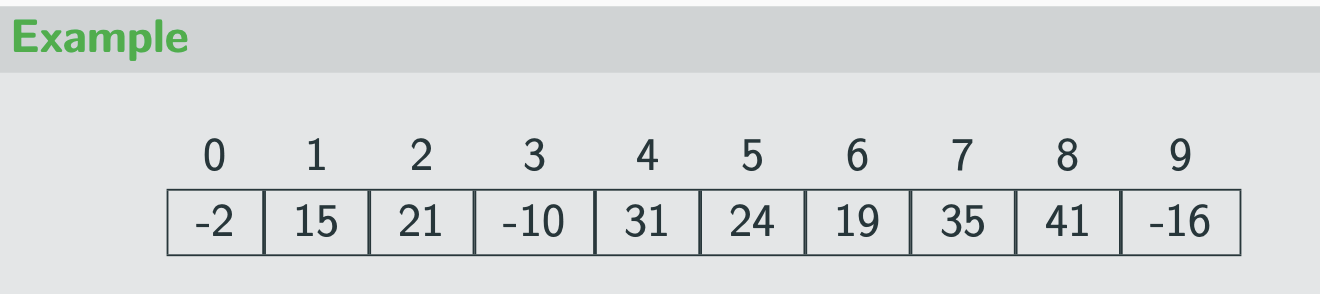
Array

sequenced collection of variable of the same type

equals(A,B) 

Return true if the array A and B are equal 

fill(A, x)

stores the value x in every cell of array x

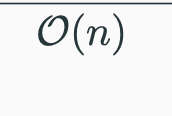
copyOf(A, n)

returns array size of n such that the first k element of this array are copied from A

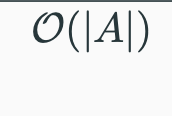
toString(A)

Returns string representation of the Array A

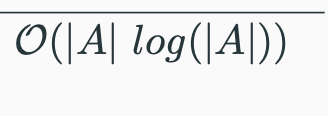
sort(A)

Sorts array based on natural ordering of its elements

binarySearch(A, x)

search the sorted array for value x returning index where its found

Stack

collection of objects of the same type which are inserted and removed

push(e)

adds element e to the top of the stack

pop()

removes and returns the top element of the stack 

top()

returns top element of stack without removing it

size()

returns number of elements in the stack

isEmpty()

returns a boolean indicating weather a stack is empty

queue

collection of objects that are inserted and removed

enqueue(e)

add element e to back of the queue

dequeue()

removes and returns the first element in the queue

first()

returns the first element of the queue without removing it

size()

return the number of elements in the queue

isEmpty()

returns a boolean indicating wether the queue is empty

list

linear sequence of elements where it can be added or removed

size() (Array lists)

Returns the number of elements in their list

 isEmpty() (Array List) 

Returns a boolean indicating weather a list is empty 

get(i) (Array List)

Returns the element of the list having index I

set(i, e)  (Array List)

Replaces element at index I with e returns old element which was replaced 

add(i, e) (Array List)

inserting element e into list moving all elements one index later

remove(i) (Array List)

Removes and returns all the elements at index I

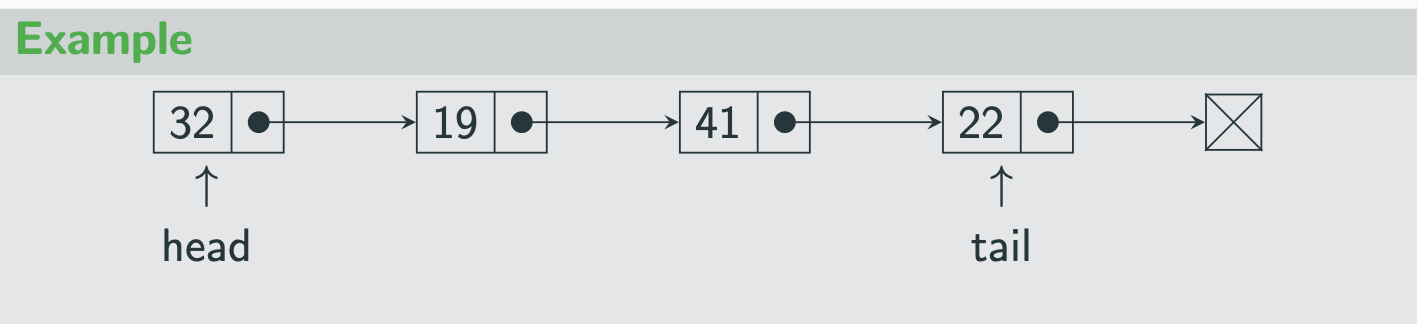
Singly linked list 

collection of nodes which form a linear sequence 

doubly linked list

node stores a reference the next and previous node

addFirst(e) (LinkedList Method)

insert the specified element at the beginning of the list

addLast(e) (LinkedList Method)

insert the specified element at the end of the list

getFirst() (LinkedList Method)

Returns the first element in the list

getLast() (LinkedList Method)

Returns the last element in the list

removeFirst()   (LinkedList Method)

Removes and returns the first element from the list 

removeLast() (LinkedList Method)

Removes and returns the last element from the list 

set(I,e) (LinkedList Method)

replaces the element I with index e and replaced element

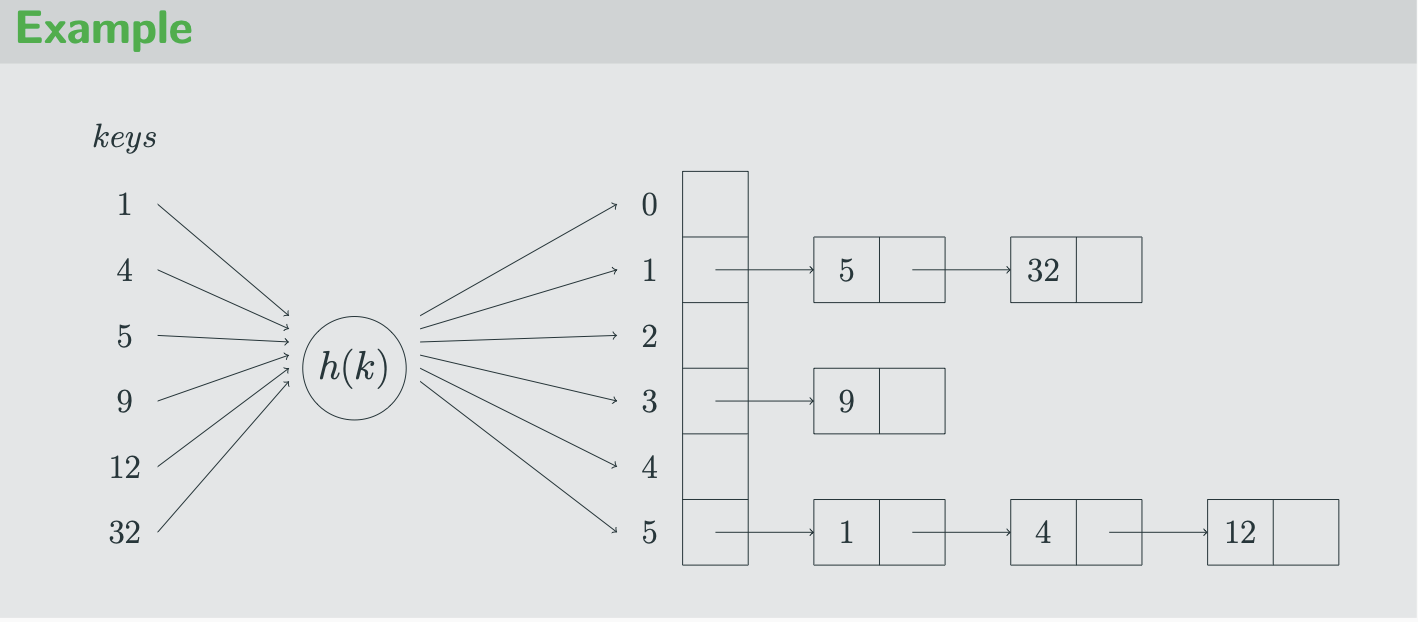
hash map

stores data in the form of keys where value pair are denoted as k and v

hash function h(k)

take key k and compute an integer

when will a collision happen

k1 = k2

what does the collision affect

insertions , deletions and searches

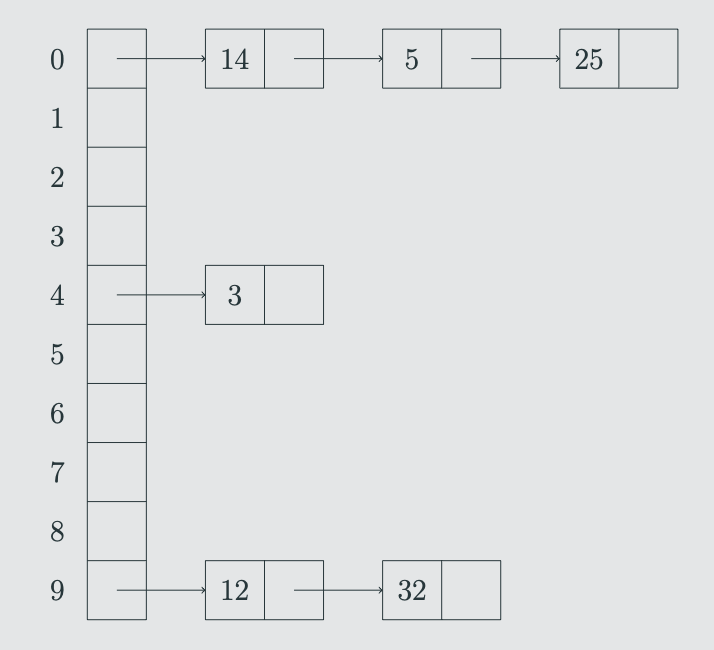
how does separate chaining solve collision issues

storing a single linked list in each index A[j]

Linear probing

is another way of dealing with collision

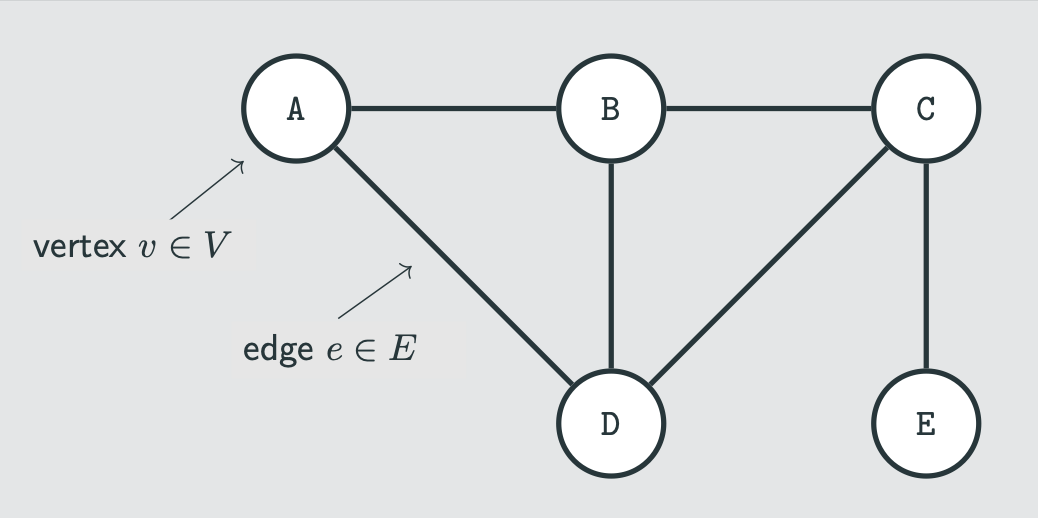
graph

finite non empty sets of points and lines

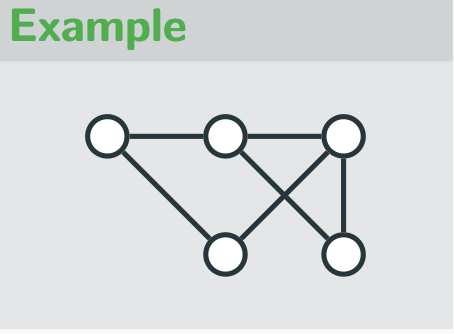
Undirected graph

edge between each vertex pair is not directed

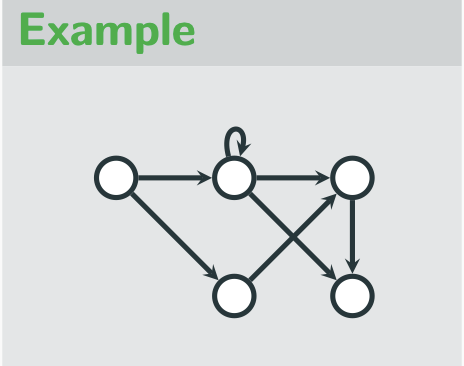
Directed graph

edge between each vertex has a direction

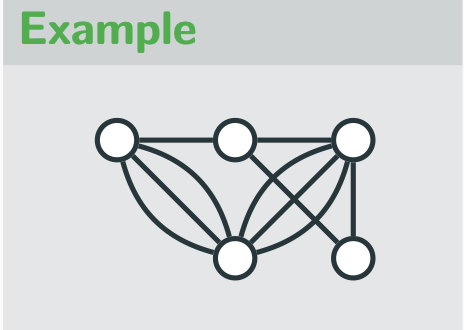
Multigraph

there is more or one edge between a pair of vertices

what is a complete graph (Kn)

simple graph with n vertices where there is an edge between every pair of distance vertices

when is a graph connected

there is a path between every pair of vertices

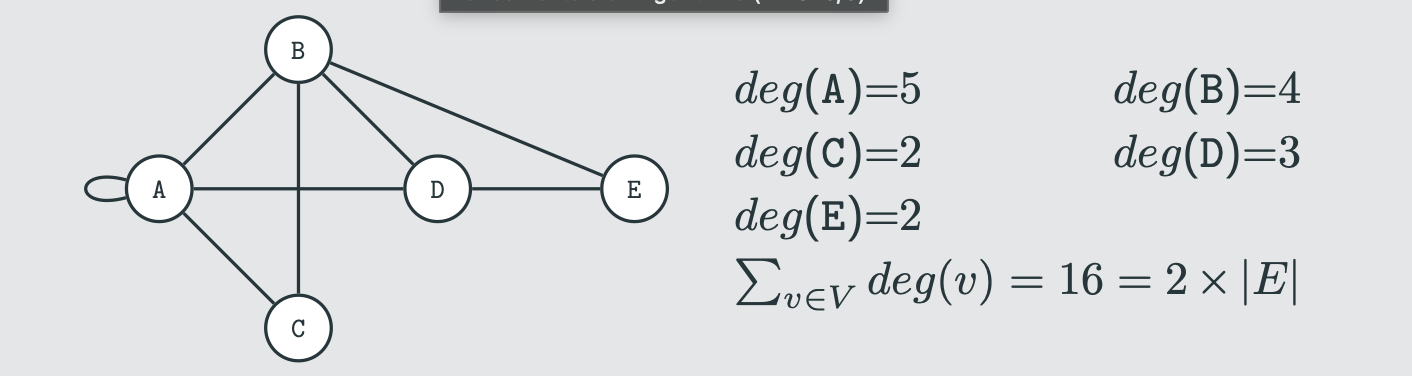
total degree

sum of degrees of all vertices

in a directed graph what is an in degree in-deg(v)

number of edges that are incoming in v

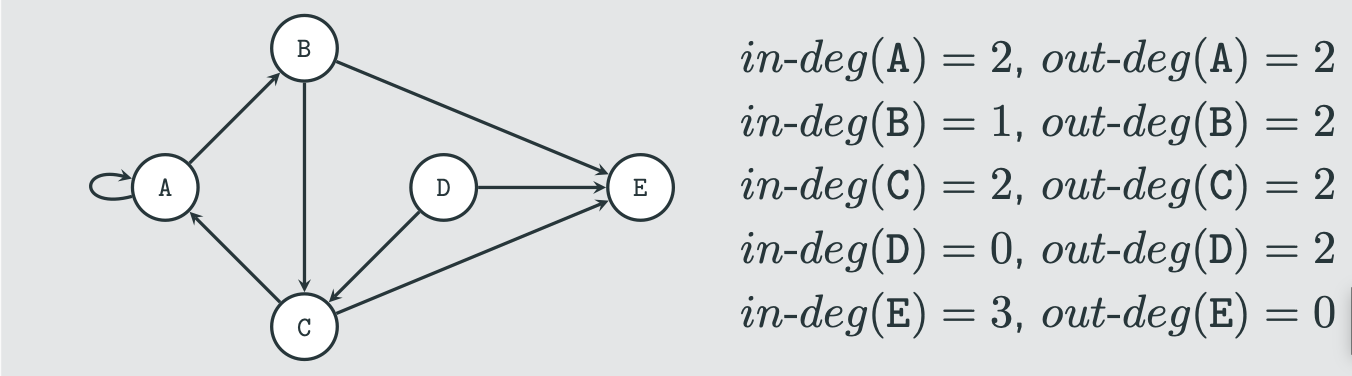
in a directed graph what is an out degree out-deg(v)

number of edges that are out coming in v

what is a circuit

path which starts and ends at the same vertex

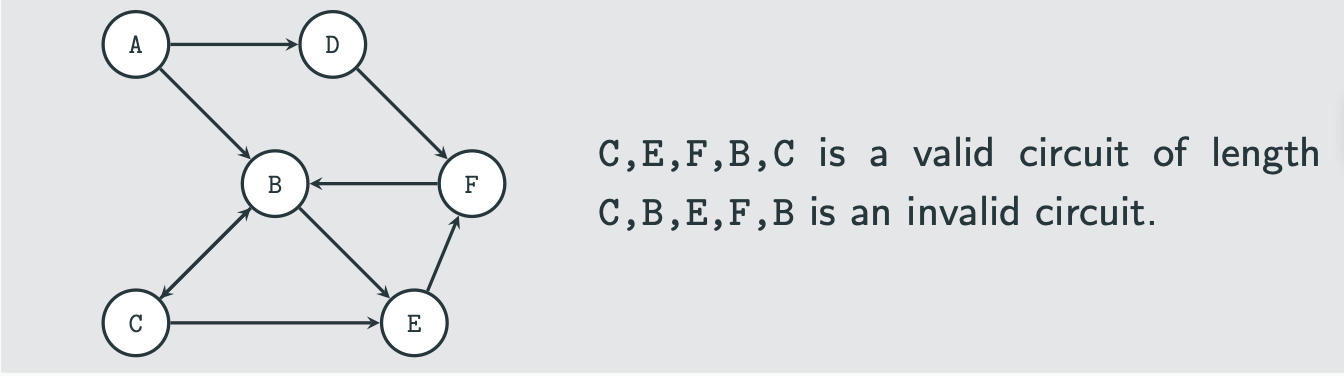
what is a cycle

circuit that contains no repeated vertices

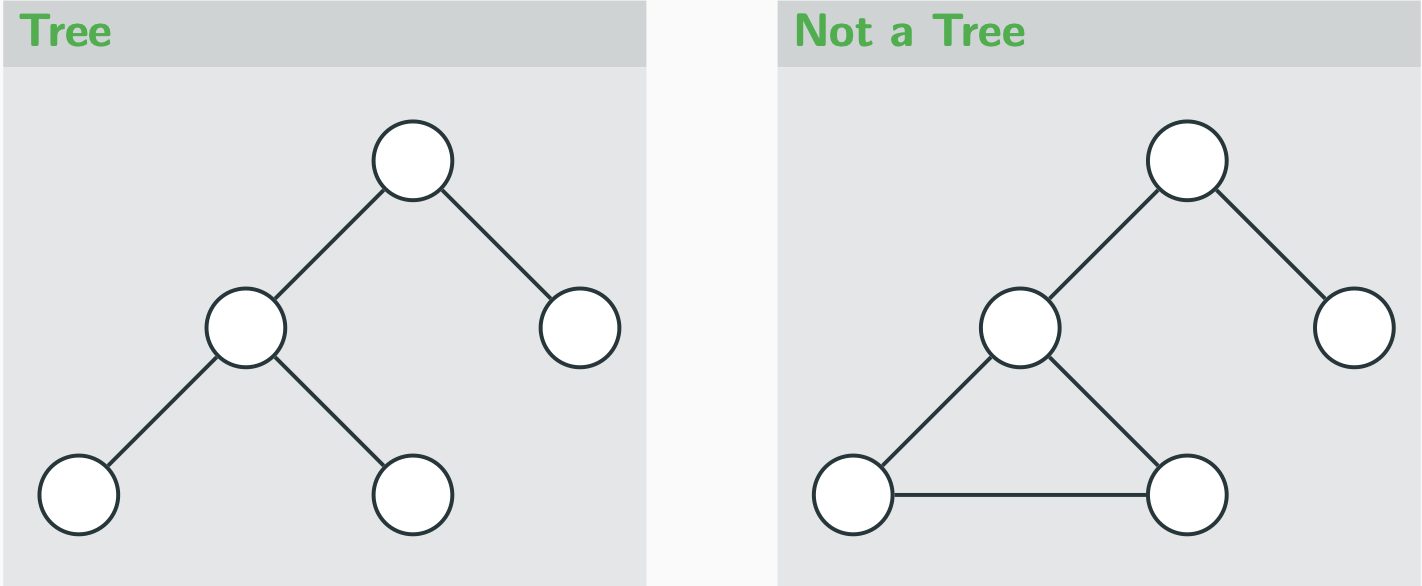
what is a tree

undirected graph that contains no cycle and is connected

Rooted trees

one vertex is specified as root

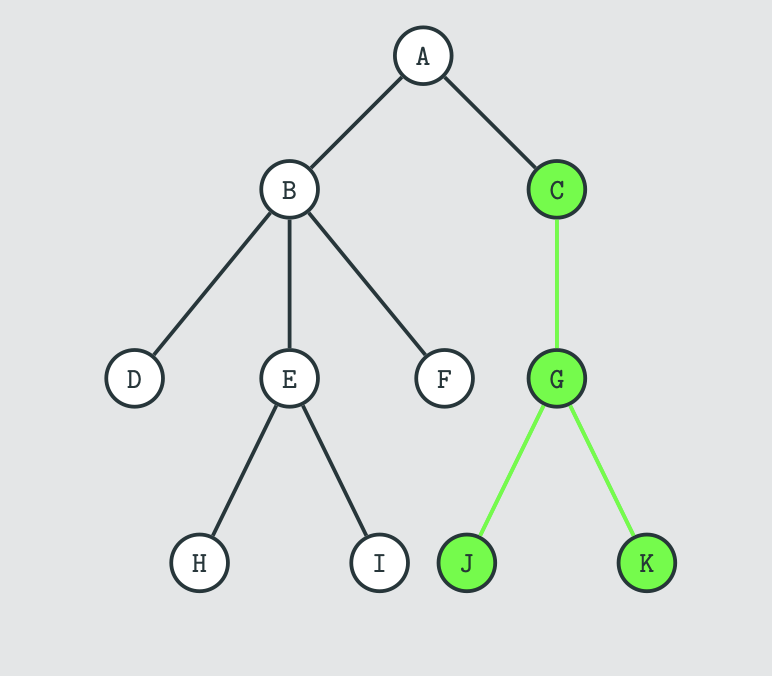
what is a subtree of tree t

tree consisting of a vertex in t and all its descendants

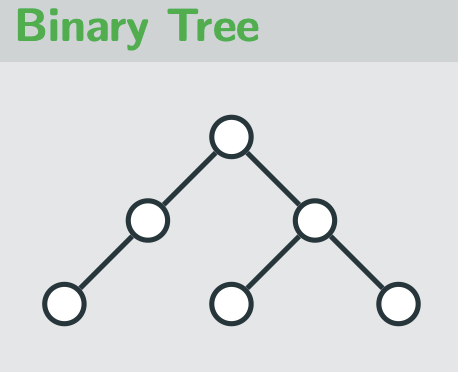
binary tree

rooted tree in which each parent has at most two children

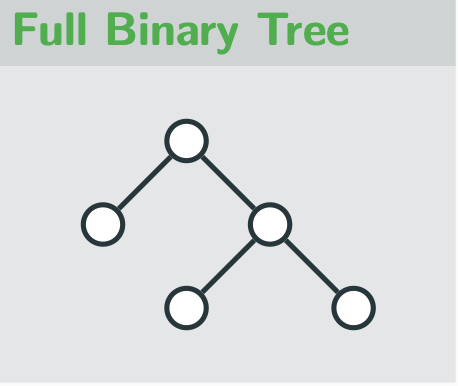
full binary tree

each parent has exactly two children

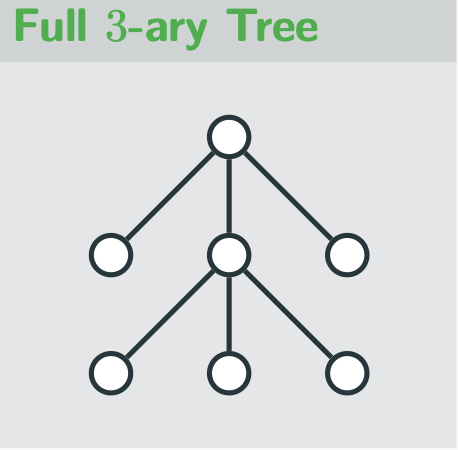
full m-ary tree

each parent has exactly m children