MAA04

Mikä on vektorin määritelmä?

vektori on jana, jolla on suuruus ja suunta

Mitkä ovat vektoreiden 2 esitystapaa?

komponenttiesitys ja tason kantavektorit

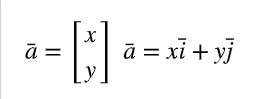
Miten kahden pisteen välinen vektori lasketaan? (kaava)

vähentämällä lopetuspiste aloituspisteestä

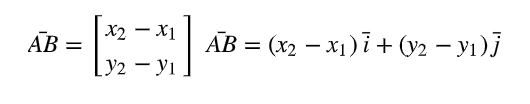
Miten lasketaan vektoreiden summa ja erotus?

HUOM! piirtäessä summavektori alkaa ensimmäisen vektorin aloituspisteestä ja loppuu toisen vektorin lopetuspisteeseen, erotuksessa jälkimmäisen vektori muutetaan se sen vastavektoriksi (v→-v) ja piirretään samalla tavalla, kuin summavektori

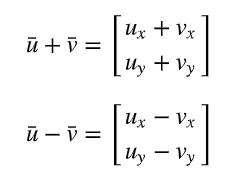
Mikä on paikkavektori?

paikkavektori alkaa origosta ja päättyy pisteeseen, ja sen komponentit ovat samat, kuin pisteen koordinaatit

Mikä on yksikkövektori?

Yksikkövektori on samansuuntainen vektori, joka on vain 1 pituinen, eli se jaetaan pituudellaan

Miten pistetulo lasketaan? (kaava)

kummankin vektorin x ja y koordinaatit kerrotaan erikseen ja sitten lasketaan yhteen

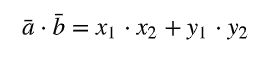
Miten vektoreiden välinen kulma lasketaan? (kaava)

HUOM! jos pistetulo on 0, vektoreiden välinen kulma on 90 astetta

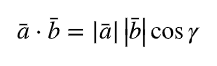
Miten vektorin pituus lasketaan?

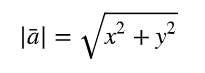
Miten itseisarvoyhtälö lasketaan?

jos vain toinen puolista on itseisarvo, otetaan itseisarvo puoli pois itseisarvosta ja tehdään toisesta puolesta plusmiinus

jos kummatkin on itseisarvoja, otetaan kummatkin pois itseisarvoista ja tehdään toisesta plusmiinus

HUOM! muista tarkistaa sijoittamalla, ja muista, että itseisarvo ei voi koskaan saada negatiivista arvoa

Miten lasketaan yhtälöryhmä?

otetaan (3 yhtälön) yhtälöryhmästä 2 yhtälöä ja ratkaistaan kuten yhtälöpari, sitten otetaan yksi sama ja jäljelle jäävä yhtälö ja ratkaistaan ne

HUOM! muista tarkistaa sijoittamalla ainakin yhteen alkuperäiseen yhtälöön

Miten lasketaan janan pituus?

joko vektoreilla (2 pisteen välisen vektorin pituus), pytagoraan lauseella (akselit toimivat kateetteina) tai kaavalla

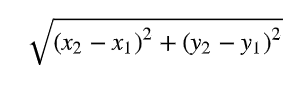
Miten lasketaan janan keskipiste?

janan keskipiste = janan pisteiden keskiarvo

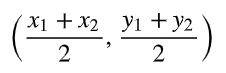
Miten parametrimuotoinen käyrän yhtälö merkitään ja ratkaistaan?

Jos pitää esim selvittää onko piste käyrällä, sijoitetaan pisteen koordinaatit omiin yhtälöihinsä x ja y paikalle. Jotta piste on käyrällä, täytyy kummankin yhtälön saada sama vastaus. Voi myös laskea mitä koordinaatteja käyrä saa tietyillä t:n arvoilla, ja tällöin sijoitetaan t:hen arvo.

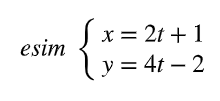
Miten käyrän leikkauspisteet voidaan määrittää matemaattisesti? Entä geogebralla?

matemaattisesti yhtälöparilla laittamalla kummatkin yhtälöt yhtälöpariin, ratkaisemalla sen normaalisti (kummankin yhtälön pitää olla =0?) ja saamalla niistä saman vastauksen, geogebralla leikkauspiste(eq1, eq2)

Mitä on käyräparvet ja miten niitä merkitään ja lasketaan?

käyräparvet ovat useamman käyrän muodostama joukko, eli yhtälöitä joissa on ainakin 1 parametri (esim a), ja ne lasketaan sijoittamalla yhtälöön piste, ja ratkaisemalla parametri

Miten kulmakerroin lasketaan y = kx + b muotoisesta (ratkaistu muoto) suoran yhtälöstä?

(b on vakio, eli missä suora leikkaa y-akselin)

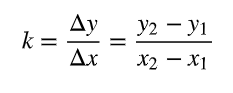
Miten lasketaan suoran suuntakulma?

suoran suuntakulma on arctan(k)

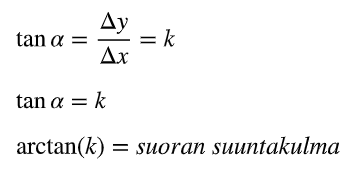
Mikä on suoran yhtälön normaalimuoto?

ax+by+c=0, jonka voi kirjoittaa muotoon y = kx + b laittamalla muut kuin y:n yhtälön oikealle puolelle: y = (-ax)/b - c/b

Miten suorien välinen kulma lasketaan?

joko laskemalla kummankin suoran suuntakulman ja vähentämällä betan gammasta tai käyttämällä kaavaa (kunhan suorat ei ole 90 asteen kulmassa toisistaan)

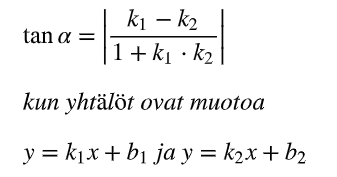
Miten suoran yhtälö voidaan laskea kulmakertoimella ja esimerkkipisteellä?

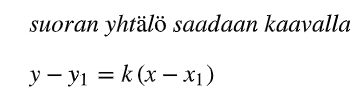
Miten pisteen etäisyys voidaan laskea suorasta?

lyhyin matka pisteestä suoraan on muodostamalla jana, joka alkaa pisteestä ja loppuu suoraan ollen siitä kohtisuorassa, janan pituus on siis pisteen etäisyys suorasta, pisteen etäisyys suorasta lasketaan kaavalla

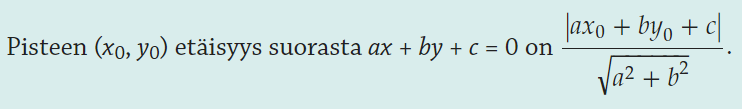
Miten pisteen etäisyys akselin suuntaisesta suorasta lasketaan?

jos suora on akselin suuntainen, ei tarvitse käyttää kaavaa, vaan voi laskea pisteen toisen ja suoran pysyvän (eri koordinaatin, eli jos suora on y:n suuntainen niin sen x koordinaatti) ja pisteen saman koordinaatin itseisarvon erotuksesta eli |x-x| tai |y-y|

Milloin suorat ovat kohtisuorassa toisiinsa?

kun niiden kulmakertoimien tulo on -1 (eli k₂ =1/k1 tai k1*k2=-1)

Miten pisteiden välinen etäisyys lasketaan?

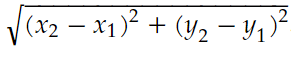
Miten ympyrän keskipistemuotoinen yhtälö lasketaan?

jossa x(0) ja y(0) ympyrän keskipiste

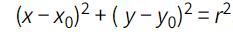
Miten laskea TiNspirellä ympyrän keskipistemuotoinen yhtälö yleisestä yhtälöstä?

kirjoita komento completesquare(ja sulkuihin yhtälö, ,x,y)

Mikä on ympyrän yleinen yhtälö?

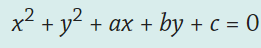
Miten ympyrän yhtälön saa keskipistemuotoisesta yleiseen?

täydentämällä muistikaavat

Miten selvitetään ympyrän yleinen yhtälö kolmesta pisteestä sen kehällä?

kaikkien pisteiden täytyy toteuttaa sen yhtälö, joten tehdään yhtälöryhmä, jossa sijoitetaan pisteet x:n ja y:n kohdalle ja ratkaistaan a, b ja c

Milloin suora on ympyrän tangentti?

kun sen etäisyys ympyrän keskipisteestä on ympyrän säde

Miten kahden ympyrän leikkauspisteet selvitetään?

laitetaan niiden yhtälöt yhtälöpariin, josta tulee suoran yhtälö, joka sijoitetaan toiseen alkuperäisistä yhtälöistä, jolloin tulee toisen asteen yhtälö, josta ratkaistaan x normaalisti

Miten paraabelin huippu lasketaan?

x=-b/2a tai nollakohtien keskiarvo

Mikä on paraabelin huippumuotoinen yhtälö?

y-y₀=a(x-x₀)²