Electric Potential and Capacitance

Electric Potential

Work done by an external force in bringing a unit positive charge from infinity to a point

Potential due to a Point Charge

V=Kq/r

Potential Due To An Electric Dipole

(derivation)

V=Kpcosθ/r²

Potential Due To A System Of Charges

V=V₁+V₂+V₃…+Vₙ

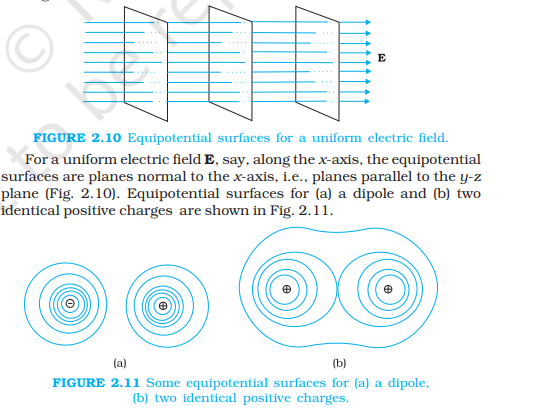
Equipotential Surfaces

• An equipotential surface is a surface with a constant value of potential at all points on the surface

• For any charge configuration, equipotential surface through a point is normal to the electric field at that point

Potential Energy Of A System Of Charges

Two charges,

U = Kq₁q₂/r

Three charges,

U = K[ q₁q₂/r₁₂ + q₂q₃/r₂₃ +q₁q₃/r₁₃ ]

Potential Energy In An External Field

Single charge:

W=qv

System of two charges:

W = q(V2-V1)

A dipole:

U = -pEcosØ

Relation between E and V

E = -dV/dr

Electrostatics of Conductors

- Inside a conductor, the electrostatic field is zero since, in the static situation, the free charges distribute themselves in such a way that the electric field cancels out everywhere inside the conductor.
- At the surface of a charged conductor, electrostatic field must be normal to the surface at every point, E=σ/εₒ (n-cap)
- Under static conditions, all the charges in a conductor lie on the surface
- The potential inside a conductor which is charged is non-zero and it equals to potential on the surface
- Inside a cavity, electric field is zero and it is protected from external electric field. This is known as electrostatic shielding

Dielectrics

• Non-conducting materials that have bound charges

• In the presence of an external electric field, charges slightly shift from their average equilibrium positions

• Polarised by applied electric field

• Types of dielectric: polar and non polar

Types of Dielectrics

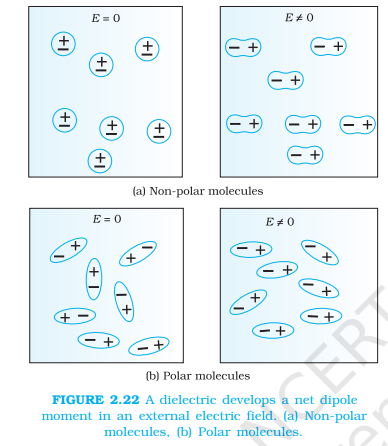
1. Polar Molecule

   • +ve and -ve charge centre don’t coincide

   • permanent dipole movement

   • H₂O, HCl

2. Non-Polar Molecule

   • +ve and -ve charge centre coincides

   • induced dipole moment

   • H₂, CO₂

image: E=0: No external field applied, E ≠0: External field is applied

Effect of dielectric

See table in cw

Polarisation

Dipole moment per unit volume

P = ε₀χE

Capacitance

C = Q/V F (Farad)

Parallel Plate Capacitor

Two parallel plates separated by a distance d
(derivation)

E = σ/ε₀
V = σd/ε₀
c = ε₀A/d

Effect of Full Dielectric on Capacitance in Parallel Plate Capacitor

c = ε₀A/d * K

Effect of Partial Dielectric on Capacitance in Parallel Plate Capacitor

c = ε₀A/d-t+(t/k)

Spherical Capacitor

c = 4πε₀R

Combination of Capacitors

Series:

1/cₛ = 1/c₁ + 1/c₂ +1/c₃

For n identical capacitors: cₛ = c/n

Parallel:

cₚ = c₁ + c₂ +c₃

For n identical capacitors: cₚ = c x n

Energy Stored in Capacitor

Work done to move charge from battery to capacitor will be stored as potential energy

U = ½ Q²/C

U = ½ CV²

U = ½ QV

Energy Density

Energy Stored/Volume

U = ½ ε₀E²