AP Physics C Mech Exam Cram

Other Uniformly Accelerated Motion Equation

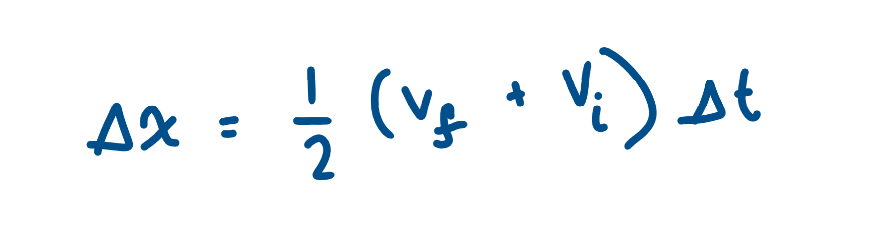
Force of Gravity Perpendicular to an Incline

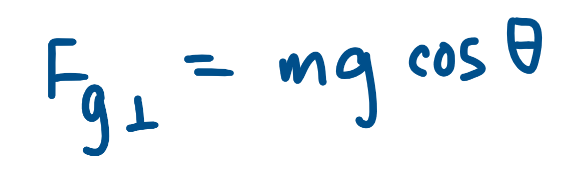
Force of Gravity Parallel to an Incline

Work/Kinetic Energy

Conservation of Mechanical Energy

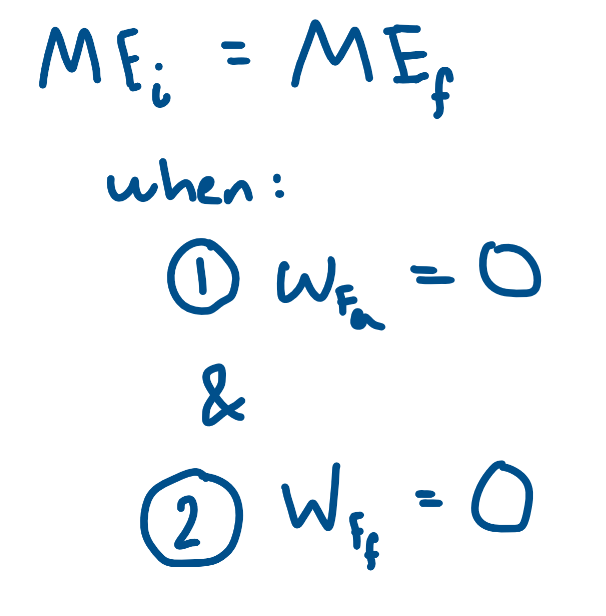
FORCE!!! ALMOST GUARANTEED TO SHOW UP ON AP EXAM

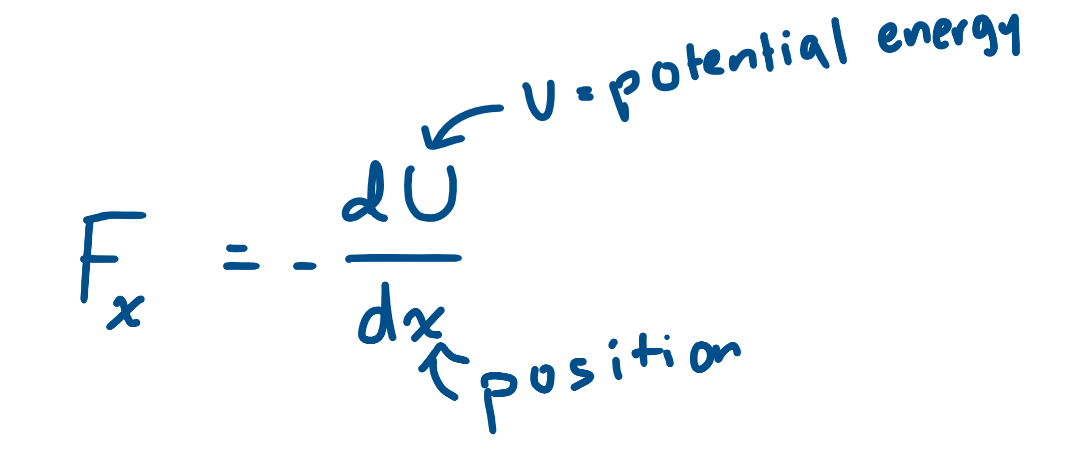
Center of Mass of a Rigid Object with Shape

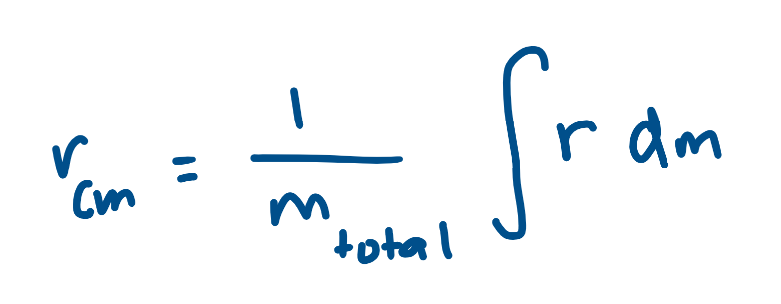
Newton’s 3 Laws

Inertia, F=ma, Action/Reaction

Kepler’s 3 Laws

1. Law of Oval Paths (planets move in elliptical orbits with the sun as one of the foci/centers of the ellipse)

2. The Law of Speedy Corners (planets “sweep” [like a windshield wiper] same area of space in the same amount of time, regardless of their place in orbit)

3. The Law of Far & Slow, Near & Quick (a planet’s orbital period is proportional to the orbital size)

Impulse

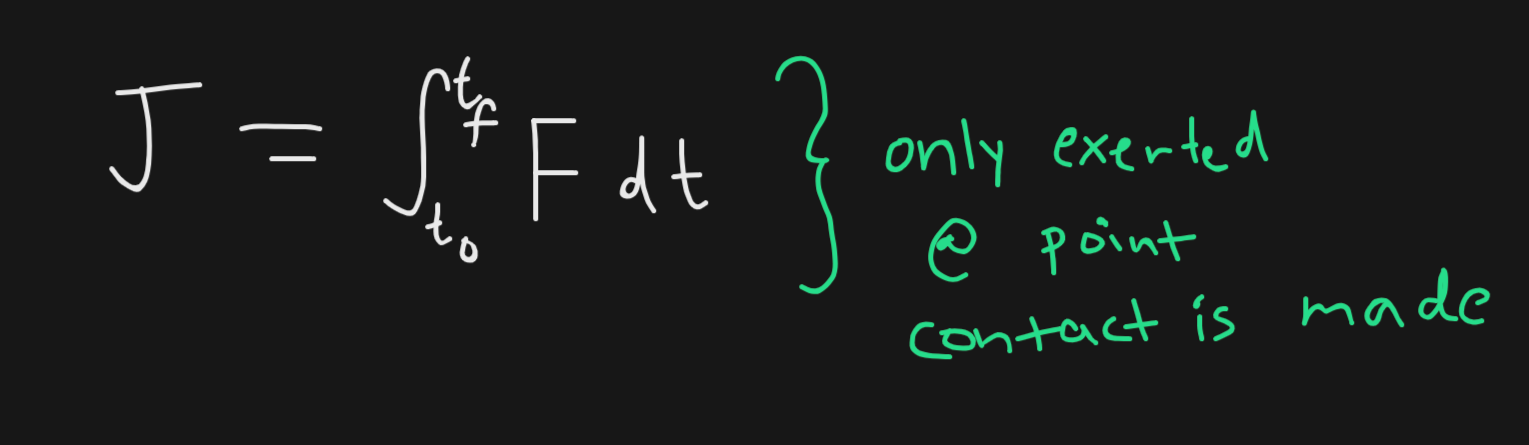
Newton’s Universal Law of Gravity

Kepler’s First Law

Kepler’s Second Law

Kepler’s Third Law

Rotational Mass/Moment of Inertia

∫r²dm

For rods, remember λ = m/L = dm/dx, rearrange to make λ dx = dm, therefore (m/L)dx = dm

Also, pay attention to the rotational axis — will determine the limits of the integral

Parallel Axis Theorem (NOT ON EQUATION SHEET)

I = Icm + mD²

If yk the moment of inertia of a rigid object abt its center of mass and that object has uniform density, you can figure out the moment of inertia abt some other axis using this theorem

Torque

T = r Fsinθ

Where r is distance from AOR, F is applied force, and theta is angle between F and r

Dot Products

Cross Product

Where unit vector n is perpendicular to BOTH a and b