Energy in Simple Harmonic Motion

Deformation

Change in the shape or size of an object due to applied forces.

work

To produce deformation in an object, we must do ____.

force, exerted, distance

Whether you pluck a guitar string or compress a car’s shock absorber, a _____ must be _______ through a _______.

That all the work is initially stored in the deformed object as some form of potential energy.

What should be concluded when the only result of the work is deformation, and no work goes into thermal, sound, or kinetic energy?

Conservative force

The force on the spring is what type of force?

Potential energy

The energy stored in the spring when the spring is extended or compressed, is what type of energy?

W = ∫(from xi to xf) F_x dx = ∫(from xi to xf) -kxdx = [(-1/2)kx^2]from xi to xf = -[(1/2)k(x_f)^2 - (1/2)k(x_i)^2] = -[U_f - U_i] = -ΔU

Write down the integral equation showing how the block oscillates in one dimension with the force of the spring acting parallel to the motion.

It means the position at which the energy stored in the spring is equal to 0.

In the spring, what does its equilibrium position marked as x_i = 0m means?

U = (1/2)k(x^2)

Formula for the potential energy inside the spring whenever it gets stretched or compressed to a certain distance (in the deformation of the spring).

K = (1/2)m(v^2)

Equation for the kinetic energy of the mass.

simple harmonic oscillator

In ___________________, the energy oscillates between kinetic energy of the mass and potential energy stored in the spring.

dissipative

The total energy is the sum of the potential energy and kinetic energy when no ___________ forces are there, which is the case with SHM of the mass and spring system.

(1/2)k(A^2)

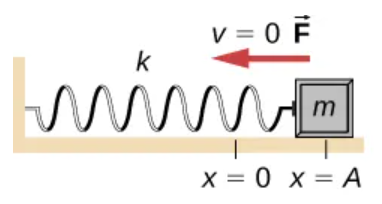
(1/2)m(-vmax^2)

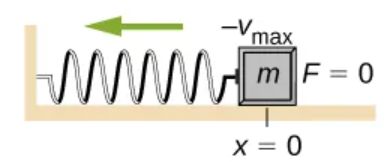
(1/2)k(-A^2)

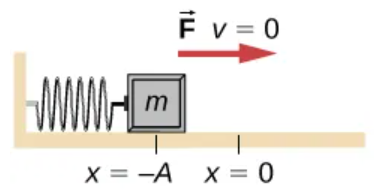
(1/2)m(vmax^2)

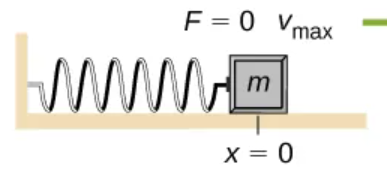
Elastic potential energy

An object on a frictionless surface attached to a spring, the motion starts with all of the energy stored in the spring as….

kinetic energy, kinetic energy, equilibrium position, elastic potential energy

As the object starts to move the elastic potential energy is converted into ______________ becoming entirely ______________ at the _______________________. Then it is converted back into ______________________, by the spring as it is stretched or compressed.

Velocity

What becomes zero when the kinetic energy is completely converted?

Etotal = U + K = ((1/2)k(x^2)) + ((1/2)m(v^2))

Equation for the total energy of the spring-block SHM system.

x(t) = Acos(ωt + Φ)

Equation for the position of the block on a spring in SHM

v(t) = -Aωsin(ωt + Φ)

Equation for the velocity of the block on a spring in SHM

(cos(θ))^2 + (sin(θ))^2 = 1

Pythagorean identity

ω = (k/m)^1/2

Formula for angular frequency in SHM

Etotal = ((1/2)k(A^2)(cos(ωt + Φ)^2)) + ((1/2)m(A^2)(ω^2)(sin(ωt + Φ)^2))

Total energy equation (Substitute the position and velocity definitions of velocity)

Etotal = ((1/2)k(A^2)(cos(ωt + Φ)^2)) + ((1/2)m(A^2)(k/m)(sin(ωt + Φ)^2))

Total energy equation;

x(t),v(t) → ω

Etotal = ((1/2)k(A^2)(cos(ωt + Φ)^2)) + ((1/2)(A^2)k(sin(ωt + Φ)^2))

Total energy equation;

x(t),v(t) → ω → simplify

Etotal = (1/2)k(A^2)(cos(ωt + Φ)^2 + sin(ωt + Φ)^2)

Total energy equation;

x(t),v(t) → ω → simplify → Factorize

Etotal = (1/2)k(A^2)

Total energy equation of a spring-block SHM, which is a constant.

(Final form)

sine-squared function

In the spring-block SHM, the kinetic energy of the block oscillates as what type of a function?

cosine-squared function

In the spring-block SHM, the potential energy stored in the spring oscillates as what type of a function?

Yes, it is true

Is it true that the total energy for the Spring-Block SHM system is constant and is proportional to the amplitude squared?

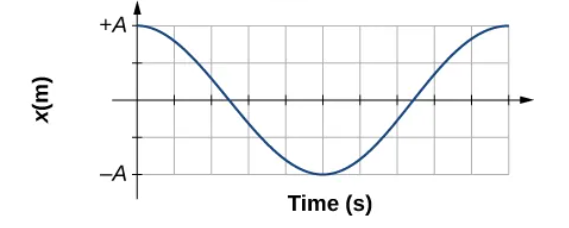
SHM Position v/s Time graph

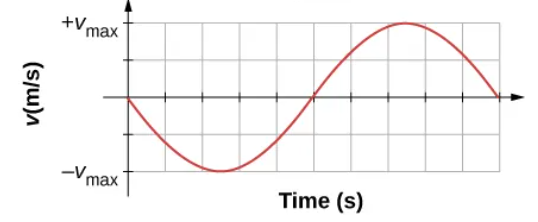
SHM Velocity v/s Time graph

(1/2)k(A^2)

1A

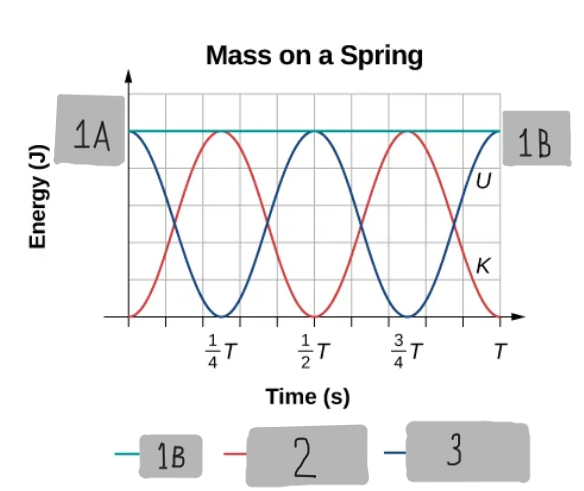
Etotal

1B

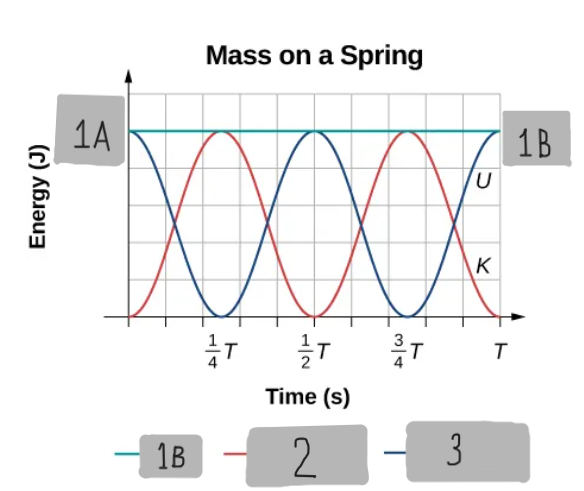
K = (1/2)m(v^2)

2

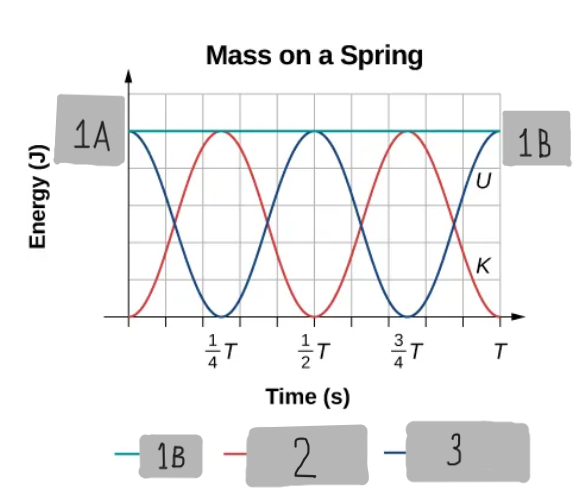
U = (1/2)k(x^2)

3

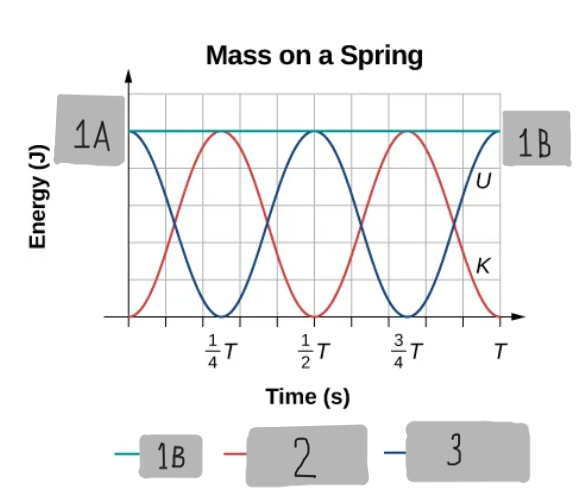
zero, maximum, equilibrium position, speed

When the kinetic energy is maximum, the potential energy is ____, This occurs when the velocity is ________ and the mass is at the ______________. Potential energy is maximum when the _____ is zero.

As a function of time or As a function of position

Two ways to graph the energy of SHM