Limits of Functions

What is the definition of a limit at a point?

Let f be a real function, a a point in its domain (or a limit point of it). We say lim_{⁡x → a} f(x) = A if for every ε > 0, there exists a δ > 0 such that whenever 0 < |x − a| <δ, we have |f(x) − A| < ε.

This means we can make f(x) as close as we want to A by making x sufficiently close to a, but not equal to it.

Prove lim⁡_x→0x = 0

Let ε > 0. Choose δ = ε.
If 0 < |x − 0| < δ, then |x − 0| = |x| < ε
Hence the limit holds.

Prove lim⁡_x→0|x| = 0

Let ε > 0. Choose δ = ε. If 0 < ||x| - 0| < δ then ||x| − 0| = |x| < ε. Hence the limit holds.

Prove lim⁡_x→82x = 16

We need |2x − 16| < ε
⇔ |x − 8| < ε/2

Prove lim_x→8​(10x − 2) = 78

We need |(10x − 2) − 78| = 10|x − 8| < ε
So choose δ = ε/10. ✅

What is the squeeze theorem?

Let f, h, g be real functions.
If for some α > 0, f(x) ≤ h(x) ≤ g(x) ∀ x ∈ (x₀ − α, x₀ + α)∖{x₀},

and lim_⁡x→x0f(x) = lim⁡_x→x0g(x) = A,

then

lim⁡_x→x0h(x) = A.
Basically if h(x) is trapped between two functions that both tend to the same limit, it must tend to that same limit.

What is a right hand limit?

lim_x→a⁺​f(x) = A means f(x) → A as x > a and x → a

What is a left hand limit?

lim_x→a^-​f(x) = A means f(x) → A as a > x and x → a

When does the two-sided limit exist?

iff both one-sided limits exist and are equal.

When do we write lim_⁡x→∞f(x) = L?

If for every ε > 0 there exists M > 0 such that x > M ⇒ |f(x) − L| < ε. (As x grows very large, f(x) gets arbitrarily close to L)

When do we write lim⁡_x→−∞f(x) = L?

If for every ε > 0 there exists N > 0 such that x < −N ⇒ |f(x) − L| < ε. (As x grows very large, f(x) gets arbitrarily close to L)

How do we write an infinite limit?

We write lim_⁡x→x0f(x) = ∞ if ∀ M > 0, ∃ δ > 0 such that 0 < |x − x₀| < δ ⇒ f(x) > M which means f(x) increases without bound as x approaches x₀.

When do we write lim⁡_x→∞f(x) = ∞?

If for all M > 0, there exists N > 0 such that x > N ⇒ f(x) > M

What is the definition for lim_x→x0⁺f(x)?

For every ε > 0 there exists δ > 0 such that |f(x) - A| < ε whenever x₀ < x < x₀ + δ

What is the definition for lim_x→a^-f(x)?

For every M > 0 there exists δ > 0 such that f(x) < -M whenever a - δ < x < a

What is the definition for lim_x→∞f(x) = A?

For every ε > 0 there exists k > 0 such that |f(x) - A| < ε whenever x > k

What is the definition for lim_x→af(x) = -∞?

For every M > 0 there exists δ > 0 such that f(x) < -M whenever 0 < |x - a| < δ

What is the definition for lim_x→-∞f(x) = ∞?

For every M > 0 there exists k > 0 such that f(x) > M whenever x < k

What is the definition for lim_x→x0f(x) = A?

For every ε > 0 there exists δ > 0 such that |f(x) - A| < ε whenever 0 < |x - x₀| < δ

What is the definition for divergence to infinity lim_x→x0f(x) = ∞?

For every M > 0 there exists δ > 0 such that f(x) > M whenever 0 < |x - x₀| < δ

What is the definition for the non-existence of a limit?

There exists ε₀ > 0, such that for every δ > 0, there exists x_δ with 0 < |x - x_δ| < δ for which |f(x_δ) - A| > ε₀

What are the key limits?

What is the algebra of limits?

• limcf(x) = c(limf(x))

• lim(f(x) + g(x)) = limf(x) + limg(x)

• lim(f(x)g(x)) = (limf(x))(limg(x))

• If g(x) =/ 0, limg(x) =/ 0

• lim(f(x)/g(x)) = (limf(x))/(limg(x))

What are some more properties of limits?

• lim_x→x0c = c

• lim_x→x0x = x₀

• lim_x→x0x² = (lim_x→x0x)² ₌ x₀²

• lim_x→x0xⁿ = x₀ⁿ

• lim_x→x0(f(x))^1/2 = (lim_x→x0f(x))^1/2

What is composition?

z = f(y), y = g(x) → z = f(g(x))

What is the change of variable theorem?

If lim_y→y0f(y) = A and lim_x→x0g(x) = y₀ where g(x) =/ y₀ and x =/ x₀ then lim_x→x0f(g(x)) = lim_y→y0f(y) = A

What does it mean if a function f(x) is continuous at x₀?

• f(x₀) is defined

• lim_x→x0f(x) exists

• lim_x→x0f(x) = f(x₀)

• If f is defined on a closed interval [a, b] = {x ∈ R ; a \< x₀ \< b} lim_x→a⁺f(x) = f(a) and lim_x→b^-f(x) = f(b)

What are the properties of continuous functions?

If f(x) and g(x) are continuous,

• f + g, f - g, f ^. g and f/g when g =/0 are all continuous

• f(g(x)) is continuous

• If f has an inverse on [a, b] then f^-1 is also continuous

What are elementary functions?

A composition of a finite number of arithmetic operations (+, -, ^. , /), exponentials, trig, logarithms, constants, power functions and inverse trig

What is the continuity of elementary functions?

All elementary functions are continuous on their domain

What is a bounded function?

We say f : A → R is bounded if the set f(A) ⊆ R is a bounded set i.e. there exists M > 0 such that -M < f(x) < M for all x in A.

What is the Intermediate Value Theorem?

Let f : [a, b] → R be continuous. Suppose f(a) < 0 < f(b). Then there exists a c in (a, b) such that f(c)= 0

What are some more notable limits?

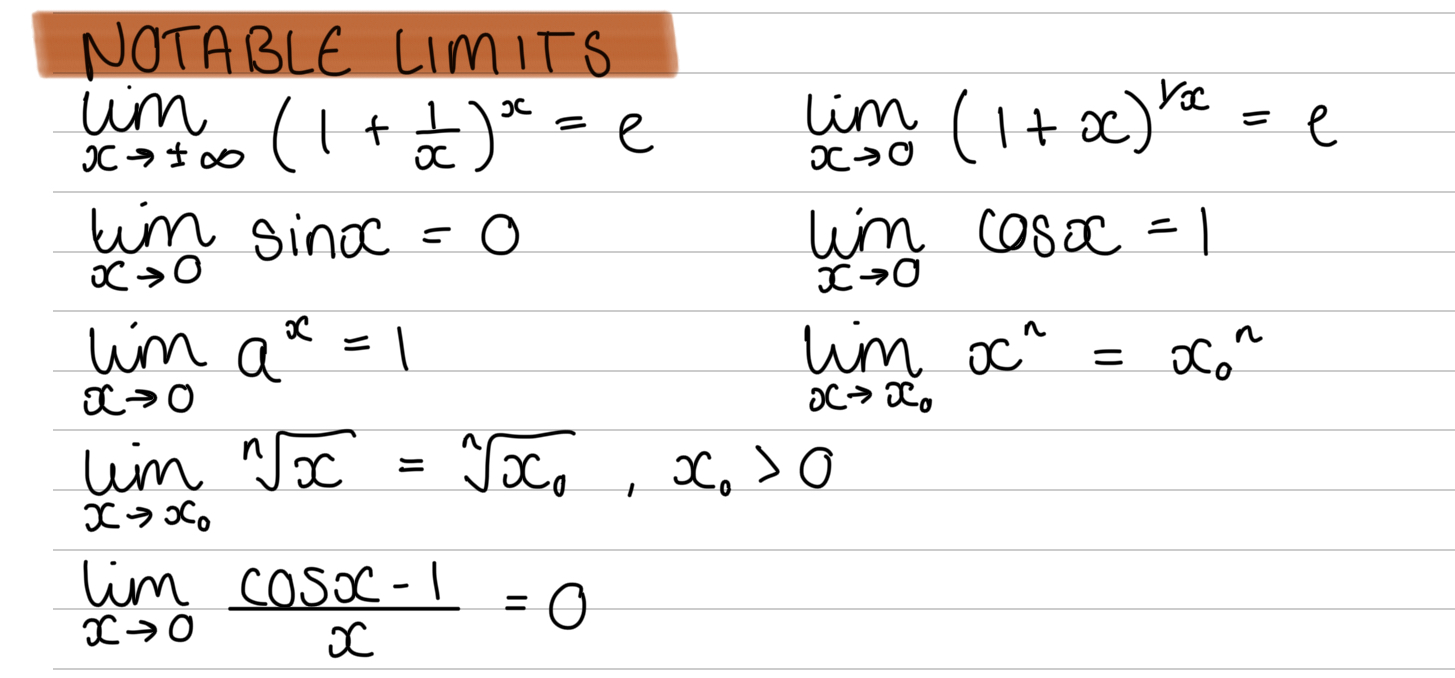
Define what it means for f to be a function from X to Y

A function f from X to Y assigns to each element x∈X exactly one element f(x)∈Y

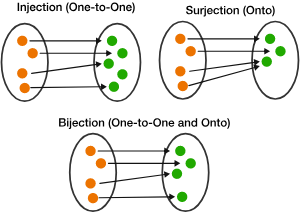
Injective vs surjective vs bijective functions

• Injective (one-to-one): maps distinct inputs to distinct outputs (no repeats)

• Surjective (onto): ensures every element in the codomain is mapped to by at least one input (no leftovers)

• Bijective: is both, creating a perfect pairing where each input has a unique output, and every output has a unique input, meaning the domain and codomain have the same size.