RC circuits

charge, capacitor, powers

When you use a flash camera, it takes a few seconds to ______ the _________, that ______ the flash.

RC circuit

A circuit that contains both resistance and capacitance.

Two-pole switch RC circuit

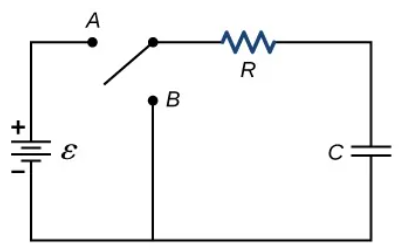
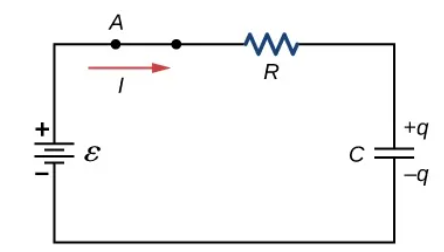
Charging capacitor

In-series connection of the voltage source, resistor, capacitor

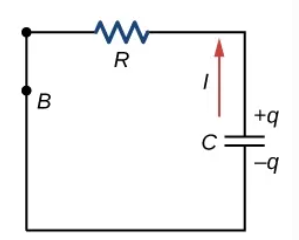
Discharging capacitors

The voltage source is being removed in this part.

C = q/V

Mathematical representation of the definition of Capacitance

Vc = q/C

Voltage across the capacitor

Vr = I R

Formula for the potential drop across the resistor

I = dq/dt

Mathematical representation of the definition of current

ε - Vr - Vc = 0

Equation given by the Kirchhoff’s loop rule to understand the charging of the capacitor.

ε - IR - q/C = 0

Substituting the definition of Vr and Vc inside the Equation of the Kirchhoff’s loop rule to understand the charging of the capacitor.

ε - R(dq/dt) - q/C = 0

Substituting the definition of current inside the Kirchhoff’s current loop that explains the charging of the capacitor (Definitions of Vr and Vc have already been substituted)

dq/dt = (εC-q)/(RC)

Solving for “the definition of current”inside the Kirchhoff’s current loop that explains the charging of the capacitor.

∫(from 0 to q) (dq)/(εC - q) = (1/RC) ∫(from 0 to t) dt

Integrating the differential equation of the Kirchhoff’s current rule that helps us to understand the charging of capacitor.

u = εC - q

The u-substitution inside the integration equation of the Kirchhoff’s current rule that helps us to understand the charging of capacitor.

du = -dq

du inside the integration equation of the Kirchhoff’s current rule that helps us to understand the charging of capacitor.

-∫(from 0 to q) (du/u) = (1/RC) ∫(from 0 to t) dt

Integration equation of the Kirchhoff’s current rule that helps us to understand the charging of capacitor. AFTER THE substitution of u and du

ln(εC - q/εC) = -(1/RC)*t

Kirchhoff’s current rule that helps us to understand the charging of capacitor. AFTER THE integration is done.

(εC - q)/(εC) = e^(-t/RC)

The ultimate final form of the Kirchhoff’s current rule that helps us to understand the charging of capacitor.

q(t) = Cε(1 - e^(-t/RC)) = Q(1 - e^(-t/τ))

Simplifying the results from the ultimate final form of the Kirchhoff’s current rule that helps us to understand the charging of capacitor.

In an equation for the charge on the charging capacitor as a function of time.

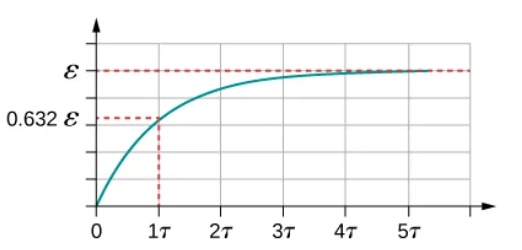
Capacitor’s Charge v/s Time function

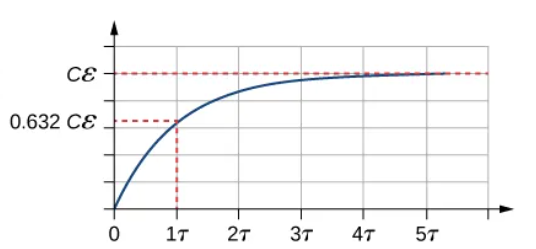
infinity, zero, slope, t = 0.0 s, zero

Capacitor’s Charge v/s Time function shows that as time approaches ________, the exponential goes to ____. The _____ of this graph is large at time ______ and approaches ____ as time increases.

decreases

As the charge on the capacitor increases, the current through the resistor _________

I(t) = dq/dt = d[Cε(1-e^(-t/RC))]/dt

Substituting the equation for the charge on the charging capacitor as a function of time inside the mathematical representation of the electrical current

I(t) = Cε(1/RC)e^(-t/RC) = (ε/R)e^(-t/τ) = I0e^(-t/τ)

Derivation of the formula for the current in the resistor inside the RC circuit.

1 - e^(-1) = 1 - 0.368 = 0.632

At time t = τ = RC, the charge is equal to ________ of the m

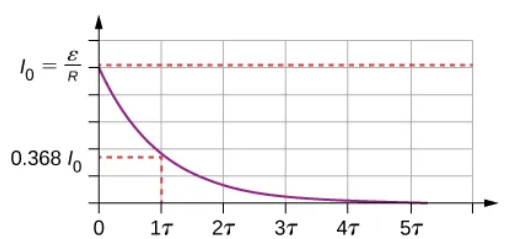
Resistor’s Current v/s Time function

Capacitor’s Voltage v/s Time function

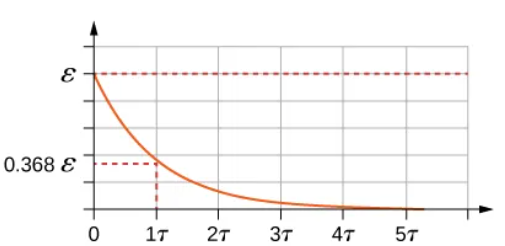
Resistor’s Voltage v/s Time function

Q = Cε

Max. Charge formula

I0 = ε/R

Initial current through the resistor formula at time t = 0.0s

I(t = τ) = I0*e^-1 = 0.368*I0

Inside the resistor in the charging RC circuit, at time t = τ, the current through the resistor will be I(t = τ) which will be…

I(t) = I0*e^-t/τ

Current through the charging RC circuit.

V(t) = ε(1 - e^-t/τ)

Voltage difference across the capacitor when it’s increasing

Vr(t) = (I0*R)e^-t/τ = εe^-t/τ

Voltage difference across the resistor

decreases, decreases, increases

As the charge on the capacitor increases, the current through the resistor _________ and the voltage across the resistor _________. The voltage across the capacitor _________.

-Vr - Vc = 0

Equation given by the Kirchhoff’s loop rule to understand the discharging of the capacitor.

IR + q/C = 0

Substituting the definitions of Vr and Vc in the equation given by the Kirchhoff’s loop rule to understand the discharging of the capacitor.

(dq/dt)R = -q/C

Substituting the mathematical representation of the current inside equation given by the Kirchhoff’s loop rule to understand the discharging of the capacitor (Definitions of Vr and Vc are already substituted)

q(t) = Q*e^(-t/τ); Q represents the initial charge

Charge on the capacitor (while discharging) formula

Yes, it is true

Is it true, that the charge in the capacitor during the discharge decreases exponentially from the initial charge, approaching zero as time approaches infinity?

resistance, Internal resistance, resistance, internal resistance, slower

The __________ while charging is significantly greater than while discharging.

___________________ of the battery accounts for most of the __________ while charging.

As the battery ages, the increasing ___________________ makes the charging process even ______.

Relaxation oscillator

A device consisting of a voltage source, resistor, capacitor, and neon lamp.

Used for controlling the indicator lights to flash at certain frequencies, also used for controlling the windshield wipers.

open-circuit (infinite resistance), zero resistance, capacitor, discharges

Neon lamp acts as a _____________, until it reaches a specific voltage, at that voltage, the lamp acts like a short-circuit (__________) the _________ __________ through the neon lamp and produces light. Before that it is charging the capacitor.

Functionality of the relaxation oscillator

Neon in the lamp breaks down, and allows the capacitor to discharge through the lamp, producing a bright flash.

tunnel diode, transistor

Other uses of the relaxation oscillator inside the electronic circuits where the neon lamp replaced with the __________ or ___________.

It’s like a voltage controlled switched. Normally open but when the right voltage is applied it closes and conducts

The switch can be used to turn on the another circuit (turn on light or run a small motor)

The relaxation oscillator can be used to make the turn signals or to vibrate the phone.

F = 1/T

Formula to calculate frequency.

increases, increases

Increasing the resistance ________ the RC time constant, which _________ the time between the operation of the wipers

Heart rate

Normally controlled by the electrical signals, which causes the muscles of the heart to contract and pump the blood.

Pacemaker

A device that have sensors that detects the body motion and breathing to increase the heart rate during physical activities, thus meeting the increased need for blood and oxygen.

In this device an RC timing circuit is used to control the time between voltage signals to the heart.

RC filters

Device used in the AC circuits to filter out the unwanted frequencies from the signal

555 timer

A device that provides timed voltage pulses. The time between these pulses is controlled by an RC circuit.

Rheostat

A variable resistor with a knob of slider, that gets used to control the current by adjusting the resistance in a circuit. (Is sometimes the part of an RC circuit)

output of the capacitor, voltage-controlled switch, discharging, capacitor, capacitor

Inside the windshield wipers, the ___________________ is used to control a ______________________; that normal is open but when the output reaches a certain.value it closes, energizing an electric motor, and __________ the _________. The motor causes the windshield wipers to sweep once across the windshield and the ___________ begins to charge again.