Directional Derivative and Gradient Vector

fx and fy (the x and y are subscripts) are

the rates of change of f(x, y) wrt x and y respectively

• tells us how the fn is changing if you move in a dir PARALLEL to the x-axis and y-axis respectively

directional derivative

• gives us info on the rate of change in a dir NOT || to the two axes (not fx or fy)

• ex: <1/2, 1/2> being a unit vector/direction for the derivative

let u = <a, b> be a unit vector specifiying the DIRECTION of the rate of change of f(x,y), the formula (from first principles of the derivative) of the directional derivative is:

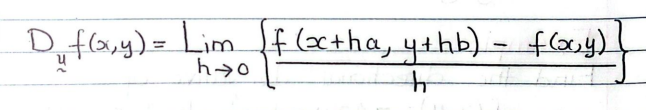
if u = <1,0> = i (a = 1, b = 0) (which is the universal horizontal unit vector), the formula for the directional derivative is:

(the deriv wrt x)

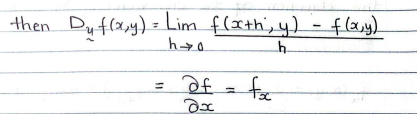
if u = <0,1> = i (a = 0, b = 1) (which is the universal vertical unit vector), the formula for the directional derivative is:

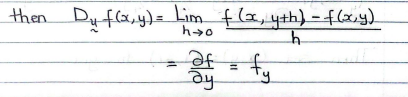
final formula for directional derivative

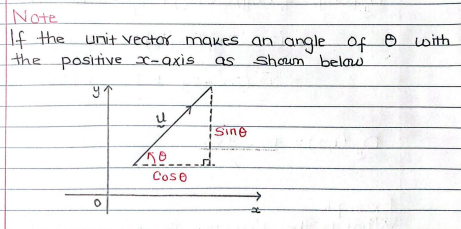
then u (the unit vec) can be written as u = <cosQ, sinQ>

• the angle must be with the POSITIVE X-AXIS

• see image for new formula

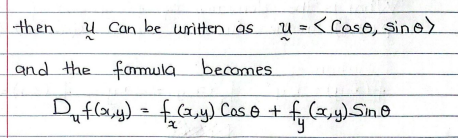
finding the unit vec b/w two points

points: P and Q

PQ = Q - P (typical cartesian subtraction)

|PQ| = dist between P and Q = sqrt(x², y²) where <x, y> = PQ

unit vec = PQ/|PQ| = <x, y>/sqrt(x², y²)

directional deriv expression

• expression incorporates the DOT PRODUCT

• dot prod of gradient vector and unit vector (MUST BE UNIT VECTOR, if it isn’t a unit vec, convert to unit vector by dividing by magnitude)

gradient vector final formula

• yields a VECTOR as the final answer

• i and j are to denote (1,0) and (0,1) respectively and should not have other nums subbed in

directional deriv w 3 vars

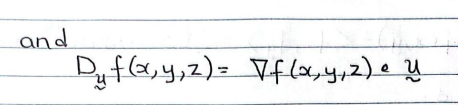
gradient vector w three vars

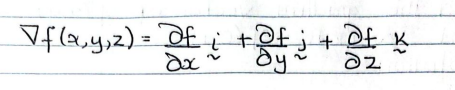
maximizing directional deriv

• suppose we have a fn w 2 or 3 vars

• and we consider ALL dir derivs of f at a given pt

• which give the rates of change of f in all possible dirs

• the question is: WHICH DIR GIVES US THE FASTEST RATE OF CHANGE and WHAT IS THE MAX RATE OF CHANGE

how to det the dir that gives us the max rate of change at a given pt

• theta = angle between gradient vec and unit vec

• max value of directional deriv occurs when theta = 0 (so cosQ = 1) therefore when the grad vec is in the same DIRECTION as the unit vec

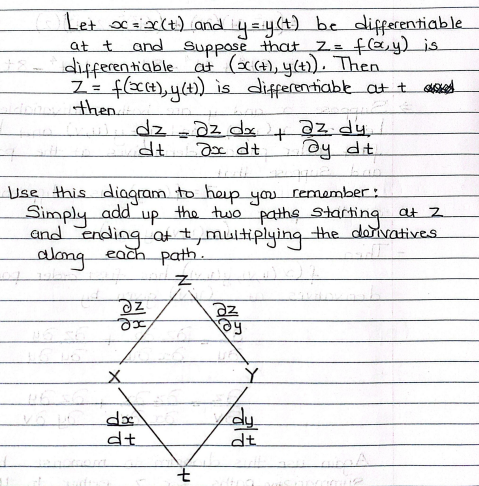
multivariable chain rule (where z = f(x,y) and x = x(t) and y = y(t))

multivariable chain rule (where z = f(x,y) and x = x(u,v) and y = y(u,v))

multivariable chain rule (where z = f(x,y) and x = x(u,v) and y = y(u,v)) DIAGRAM

implicit differentiation

alternative method for implicit differentiation involving partial derivs (Fx, Fy)

gradient vector (in simple terms)

the vector made of <value of the partial deriv wrt x at the given pt, value of the partial deriv wrt y at the given pt>

• image gives you the gradient vec in the i + j format where i reps <1,0> (unit vec parallel to x-axis) and j reps <0,1> (unit vec || to y-axis)

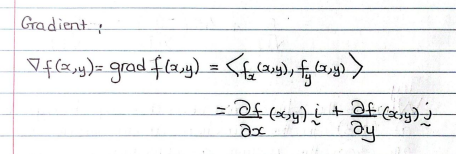
to calc max rate of change

calc the magnitude of the gradient vec