Measurements and Significant Figures

Measured Numbers

==Measured Numbers:== Numbers/Amounts that are determined using a measuring tool

(Examples includes: height or weight)

Significant Figures

==Significant Figures:== The “figures”, or digits that are important in measurements and calculations

(Simply speaking, it’s any digit that you measure plus one digit that you estimate.)

\
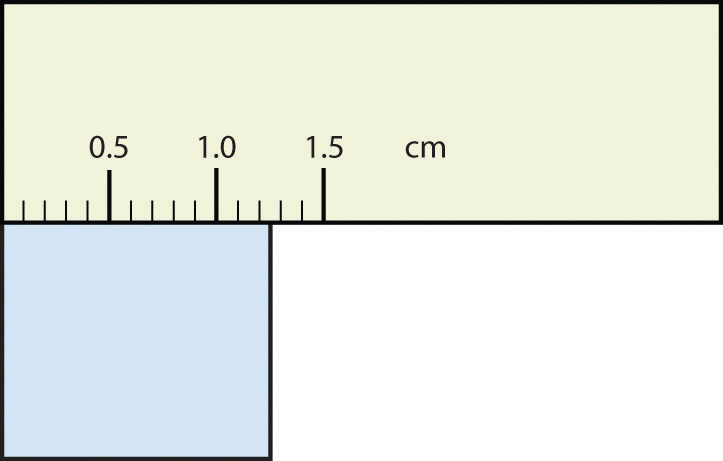
Example: The following image shows that it’s around 1.2 cm. It’s the last accurate digit in this picture. However, because they’re not perfect, we need to estimate a bit more past the last accurate digit. The following could range anywhere from 1.20-1.30… as long as it’s less than 1.30

@@What determines the number of significant figures in a Measurement?@@

1. The size of divisions on your measuring device
2. The size of the object
3. The difficulty in measuring the object

\
Which numbers are significant?

To begin, there are two types of numbers as far as significant figures are concerned: zeroes, and nonzero digits (1-9)

• ALL nonzero digits are SIGNIFICANT !
  • Example: 1,234 has four significant figures
• Some zeroes are significant, while others aren’t:
  • Leading zeroes
  • These are the zeroes in front of a number… they start it off. These zeroes NEVER count.
    • Example: 0.00001 has 1 significant figure (the 1)
  • Captive zeroes
  • These are the zeroes in between nonzero numbers. They ALWAYS count.
    • Example: 1.0091 has 5 significant figures (they all count)
  • Trailing zeroes
  • These are the zeroes at the end of a number. When a decimal point is in place, it counts… otherwise, they will not count.
    • Example: 1,000 has 1 significant figure (the 1), while 1,000.0 has 5 significant figures (all of them)

\

Exact Numbers

Exact numbers are numbers that are…

• Obtained when you count objects
• Obtained from a defined relationship
• NOT obtained with measuring tools

Example: 12 eggs in a dozen

Exact numbers are known with absolute certainty, so they’re viewed as numbers with an infinite number of significant figures

(2 could be 2.0000000000000000…)

Operations with Significant Figures

Adding and Subtracting:

• The answer has the same number of decimal places as the measurement with the fewest decimal places
  • Example:

Multiplying and Dividing:

• Round the answer to the same number of significant figures as the measurement with the fewest significant figures
  • Example:

Scientific Notation

Scientific notations are used for very large numbers, or really small numbers

• consists of a number between 1-10 followed by the power of 10
• If the number you start with is greater than 1, the exponent will be positive
  • Example: 39923 = 3.9923 x 10^4
• If the number you start with is less than 1, the exponent will be negative
  • Example: 0.0052 = 5.2 x 10^-3

Dimensional Analysis

Dimensional Analysis is a method that uses the idea that any number can be multiplied by one without changing its value

(Basically, it’s used to go from one unit to another)

• Using conversion factors, you could set an equation up and multiply them to determine the new value in a new unit
• You would have your starting value, and the conversion rate in a fraction next to it. The key to this method is to have the units cancel out, so that the value is left in the unit you want it in.
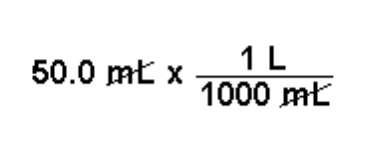
  • Example:
• Oftentimes, this means that the unit you want to convert to is on the top, while the unit you’re trying to cancel out is on the bottom.

Basic Summary

%%Exact numbers are obtained by%%

• Counting
• Definition

%%Measured numbers are obtained by%%

• Using a measuring tool

%%Significant figures are counted when%%

• Nonzero numbers
• Captive zeroes
• Trailing zeroes WHEN there is a decimal point

%%Adding/Subtracting with Significant Figures: Round to number with fewest decimal places%%

%%Multiplying/Dividing with Significant Figures: Round to number with fewest significant numbers%%

%%When using scientific notation, make sure the first number is a number from 1-10 and the exponent is a power of 10%%

\
\
\