6- Angular momentum

How is the centre of mass (COM) of a rigid body defined in terms of integrals?

M= the total mass

ρ(r)= the density

dV= the volume element.

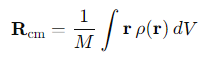
What two types of motion can an extended body exhibit?

• Translational motion of the centre of mass

• Internal motion (e.g., rotation).

What does Chasles' Theorem state about rigid body motion?

The motion of a rigid body can be described as:

1. Translational motion of the centre of mass under the total force.

2. Rotation about an axis through the centre of mass due to torques.

What determines the translational motion of the centre of mass?

The total external force applied to the body.

What is the formula for the total mass of a rigid body?

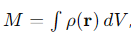
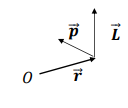
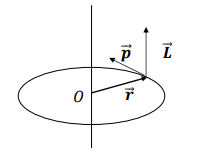
What is the formula for the angular momentum L of a point particle?

• r =the position vector

• p= the momentum.

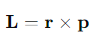
What is the formula for the magnitude of angular momentum?

• θ = the angle between r and p.

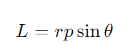
What mathematical operation is used to calculate angular momentum?

The vector cross-product.

In circular motion, how is the direction of the angular momentum vector L determined?

L is perpendicular to the plane of rotation and oriented:

• Upwards for anti-clockwise rotation.

• Downwards for clockwise rotation.

What is the formula for the magnitude of angular momentum in circular motion?

r =the radius

m= the mass

v = the linear velocity

ω=the angular velocity.

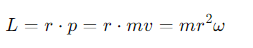
What is the angle θ between r(radius) and p (momentum) in circular motion?

θ=π/2 meaning r and p are perpendicular.

Is angular momentum conserved in uniform circular motion?

Yes

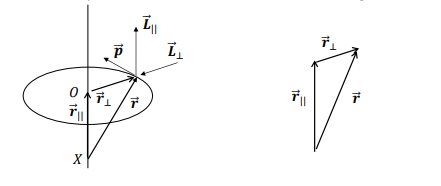
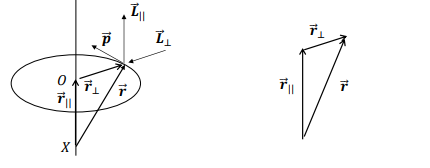
How can the position vector r of a particle relative to an external point X be expressed?

• r∣∣​ is parallel to the axis of rotation

• r⊥​ is perpendicular to the axis of rotation.

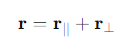
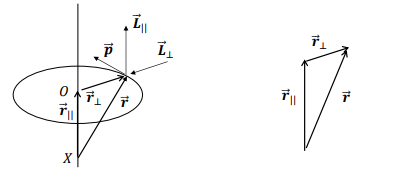
What is the expression for angular momentum L relative to a point X outside the plane of motion?

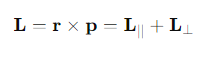
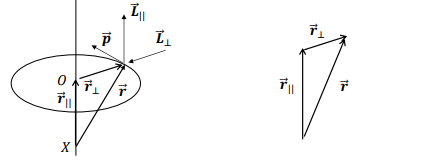
What is L∣∣​ in the context of angular momentum?

• Its the angular momentum component along the axis of rotation

• It is the same as the angular momentum about the centre of the circular motion.

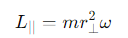
What is L⊥ in the context of angular momentum?

• Its the perpendicular component of angular momentum, which lies along r⊥​

• It swings around in the plane of rotation at the same rate as the particle.

What determines the overall angular momentum L about a point X?

Its is the vector sum of L∣∣ and L⊥

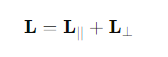
What type of motion is considered when an extended body rotates about a fixed axis?

This type of motion is called "pure rotation."

How is the total angular momentum L of the body calculated?

By summing the angular momenta of all particles in the body

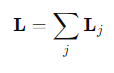
Where is the origin chosen for calculating angular momentum in the case of pure rotation?

The origin is chosen on the axis of rotation.

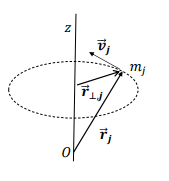
How is the angular momentum of each particle L_j​ determined?

r_j =the position vector of the particle relative to the axis of rotation

p_j​ = its linear momentum.

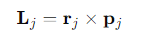
How is the component of angular momentum along the axis of rotation (L_z) for each particle calculated?

m_j​ = the mass

r⊥=the perpendicular distance to the axis

ω= is the angular velocity.

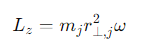
Why do all particles in a rigid body contribute angular momentum components with the same sign along the axis of rotation?

• Because all particles rotate in the same direction as the body

• This ensures their angular momentum components along the axis are aligned.

How is the total parallel component of angular momentum for the rigid body calculated?

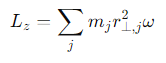
What is the final formula for the parallel component of the angular momentum of a rigid body?

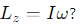
What is the coefficient of proportionality in the equation Lz=Iω?

The coefficient of proportionality is the moment of inertia (I).

What is the formula for the moment of inertia I?

• m_j​ =the mass of each particle

• r_⊥,j= the perpendicular distance to the axis of rotation.

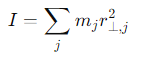
What does the moment of inertia depend on?

The distribution of masses in space and the axis of rotation.

Can the moment of inertia be the same for different bodies?

No, the moment of inertia is unique to each body depending on its mass distribution and the chosen axis of rotation.

What happens to the angular momentum of a rigid body in pure rotation in most cases?

It does not stay parallel to the axis of rotation; instead, it precesses about the axis.

Under what condition can the perpendicular components of the angular momenta of all individual particles cancel out?

When the body is rotating around a symmetry axis

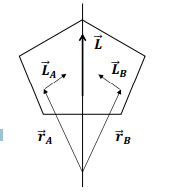
What is a symmetry axis?

An axis that passes through the body's centre of mass and for which the mass is distributed symmetrically about the axis.

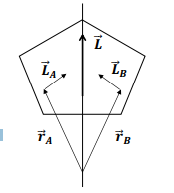
What occurs when a body rotates around a symmetry axis?

• Particles on opposite sides of the axis have their perpendicular angular momentum components cancel each other out

• This results in the total angular momentum being parallel to the axis of rotation.

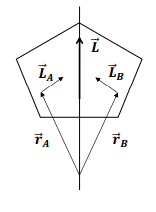
What is the general expression for the position vector of a particle in the laboratory frame of reference?

Its the sum of the vector of the centre of mass R⃗ and the radius vector r⃗_j’ in the local frame:

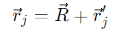
How is the angular momentum of a body in the laboratory frame defined?

v⃗_j = the velocity of the j-th particle.

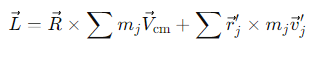
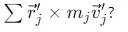
What is the significance of the last term in the angular momentum equation?

• Its the spin angular momentum of the body

• Calculated in the local frame of reference

• It is denoted as L⃗_s

What is the relationship between the angular momentum of the body in the laboratory frame and the local frame?

• M = the total mass of the body

• V⃗_cm​ is the velocity of the centre of mass.

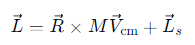
How is the total angular momentum of a rigid body expressed?

Its the sum of the angular momentum of rotation around its centre of mass (spin angular momentum) and the angular momentum of the centre of mass as a point particle around the origin (orbital angular momentum).

What is spin angular momentum?

• Its the intrinsic angular momentum of the body due to its rotation about its centre of mass.

• It is independent of the choice of coordinate system.

What is orbital angular momentum?

• Its the angular momentum of the centre of mass of the body as a point particle

• It depends on the chosen origin.

• If the origin is along the line of motion, orbital angular momentum disappears.

What does it mean for spin angular momentum to be independent of the coordinate system?

Its intrinsic to the body and does not change if the reference frame is shifted, provided the centre of mass is stationary