Unit 3: Electric Force, Field, and Potential

Electric Charge

• In an isolated system, the charge is always conserved.

• Protons and electrons have a quality called electric charge.

• The charge is invariant in nature.

• The charge is quantized.

• (Q = n e)

  • e = 1.6 * 10^-19 C

  • n = no. of electrons

  • Q = charge

Ionization

It involves addition or removal of electrons.

Coulomb’s Law

The electric force between two particles with charges q1 and q2 separated by distance r has a magnitude by the equation:

F = Kq1q2/r^2

• F = force

• K = coulomb’s constant

• q1 and q2 = charges

• r = distance between the charges

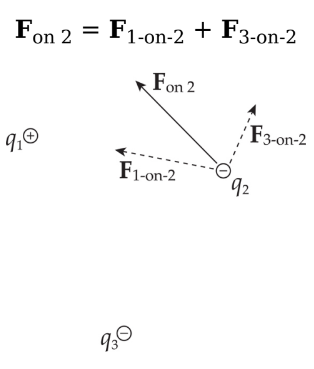
Addition of forces

Consider three point charges: q1, q2, and q3. The total electric force acting on, say, is simply the sum of F1-on-2, the electric force on q2 due to q1, and F3-on-2, the electric force on q2 due to q3:

Electric Field

The space is surrounded by a charge in which another charged particle experiences the force.

E = F on q/ q

It describes the electric field vector from the force vector on a positive charge.

Electric field due to a point charge

The electric field surrounding the point charge is:

E = 1/4πε0 * Q/r^2

• E = electric field

• Q = charger = distance between charges

• ε0 = permittivity of free space

Three types of electric field

• Radial field

• It is generated by a collection of point charges.

• An infinite sheet of charge.

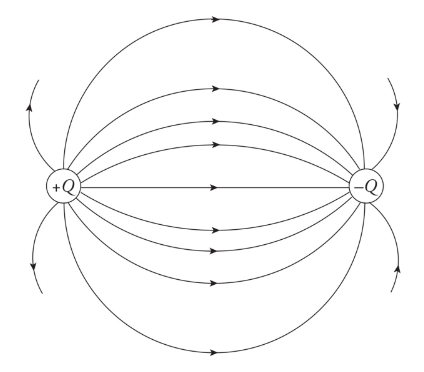
electric field lines

• The electric fields follow the same addition properties as the electric force.

• The electric field lines never cross.

The uniform electric field

A lot of problems deal with the uniform electric field. The field may be taken as uniform at least in the middle. The uniform field just signifies the constant force.

Conductors

Materials which allow the flow of excess charge without resisting it.

Insulators

Materials that resist the flow of electrons.

Charging by friction

It involves rubbing the insulator against another material, thereby stripping electrons from one to another material.

Charging through conduction

When we connect two conductors charge flows from one to another until the potential of both the conductors becomes the same.

Charging through induction

The process of charging by induction may be used to redistribute charges among a pair of neutrally charged spheres.

If the sphere is an insulator made up of glass

There aren’t any free electrons. The atoms make up the sphere will become polarised.

charge of proton

positive

charge of electron

negative

law of charges

the directions of the electric forces on the charges of mutual interaction; like charges repel, opposite charges attract.

net charge

an object with an excess of positive or negative charges

electrostatic charging

accomplished by Friction, Contact, Induction, or Polarization

Charging by Polarization

Charging by Polarization

How do objects become charged?

By gaining/losing electrons

Electric charge is always _______.

Conserved

What is the numerical value of one charge?

1 e = 1.6 x 10^-19 Coulombs

The SI unit of a charge is in ______.

coulombs

What happens when an insulator is charged?

Only the small spot which was directly contacted with a charge remains charged.

What is the name of materials that contain properties somewhere between conductors and insulators?

semiconductors

A dipole consists of:

two equal and opposite charged

In what direction to field lines go?

From positive to negative charges ALWAYS

What indicated field strength?

The density of field lines

What do few field lines between charges indicate?

a weak field

Which one of the following rules, laws, or principles describes how the net electric charge of an isolated system undergoing any process remains constant?

law of conservation of electric charge

Electrical Potential Energy

We is the work done by the electric force, then the change in the charge’s electrical potential energy is defined by:

Ue = electrical potential energy

We = work done by electric force

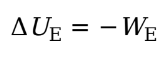
Electrical Potential Energy from a point charge

Electrical potential energy required to move along the field lines surrounding a point charge is given by:

• q1 and q2 = charges

• e0 = permeability of free space

• Ue = electrical potential energy

• r = distance

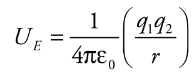
Electric Potential

Electric potential is the electric potential energy per unit of charge at a point in an electric field, measured in volts (V). It's the work done per unit charge in bringing a test charge from infinity to that point.

V = U/q

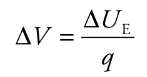
Electric Potential Energy from a point charge

Consider the electric field created by a point source charge Q. If a charge moves from a distance rA to a distance rB from Q, then the change in the potential energy is:

• Ub and Ua = electrical potential energies for a and b

• ra and rb = distances for a and b

• e0 = permeability of free space

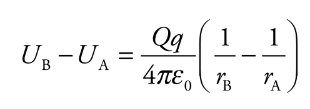
Equipotential Surface

An equipotential surface is a surface in a region of space where every point on the surface is at the same potential. In other words, no work is required to move a charge along an equipotential surface. Equipotential surfaces are perpendicular to electric field lines and can be used to visualize the electric field in a given region.

Addition of electric potential

V = kQ/r

• V = electric potential energy

• q = point charger = distance between any point around the charge to the point charge

• k = Coulomb constant; k = 9.0 × 109 N

Equipotential Curve

Equipotential curves are curves of constant elevation. If you walk along any of the contour lines and you neither ascend nor descend, then the curve is known as the equipotential curve.

Equipotential Map

A drawing of several equipotential curves at various values of the potential for a charge distribution is called an equipotential map.

Capacitor

Two conductors, separated by some distance carry equal but opposite charges +Q and -Q. The pair comprises a system called a capacitor.

Parallel-Plate Capacitor

The capacitor is in the form of parallel metal plates or sheets.

Capacitance

The capacitance measures the capacity for holding charge.

C = κε₀A/d (k = dielectric constant)

Fringing fields

Fringing fields extend beyond conductor or magnetic material edges. They weaken as the distance from the edge increases. They're important in device design but can cause interference and affect performance.

energy stored in capacitor

The energy stored in a capacitor can be calculated using the formula

Uc = ½QV = ½CV² where

U is the energy stored in joules, C is the capacitance of the capacitor in farads and V is the voltage across the capacitor in volts.

Dielectric

To keep the plates of the capacitor apart they are filled with dielectric which increases the capacitance of the capacitor.

The amount of work done by a uniform electric field

W = q E d

• W = work done

• q = charge

• E = electric field

• d = distance

A dielectric always _______ the capacitance of a capacitor

increases

the __________ of the capacitance of a collection of capacitors in series is found by adding the reciprocals of the individual capacitances

reciprocal

Collection of capacitors is said to be in ______ if they all share the same charge magnitude

series

The equivalent capacitance of a collection of capacitors in parallel is found by _______ the individual capacitances

adding

The equivalent capacitance of a collection of capacitors in parallel is found by _______ the individual capacitances

parallel

1 C/V = ?

1 Farad

Ratio of charge to potential difference (C=Q/∆V)

capacitance

Magnitude of the potential difference between two plates of a distance d

∆V = -Ed

How does the electric field relate to electric potential difference?

E = -dV/dr

1 volt = ?

1 J/C

Wₑ = Fₑdistancecosθ = qE*distance; ∆U =?

-qEd*cosθ

When a charge moves in an electric field, unless its displacement is always perpendicular to the field, the electric force does _______ on the charge.

work

Factors on which capacitance of a parallel plate capacitor depend on?

1. Area of the plates (C ∝ A)

2. Distance between the plates ( C ∝ 1/d)

3. Permittivity of medium ( C ∝ ε0)

What is the dimensional formula of capacitance?

M-1L-2T4A2

Potential energy of a dipole in a uniform electric field?

U = -pEcosθ

How to solve for capacitance?

C = q/V

What factors does capacitance depend on?

1. Size and shape of conductor

2. Nature (permittivity)

How to find total capacitance in a series combination?

1/Cs = 1/C1 + 1/C2 + 1/C3

How to find total capacitance in a parallel combination?

Cp = C1 +C2 + C3