Geometry I Honors Midterm Studyguide

What is the difference between preimage and image?

Preimage comes first

Through any three points, not on the same line how many planes are there?

One plane

Through any two points how many lines are there?

One line

What are collinear and coplanar points?

Collinear - on the same line

Coplanar - on the same plane

What is a postulate and axiom?

Postulate - a rule accepted without proof

Axiom - a rule that is accepted without proof

What do you call a nine, ten, and twelve+ sided shape?

Nine - nonagon

Ten - decagon

Twelve - dodecagon

Twelve plus - n - gon

What is a convex and concave polygon?

What is a converse?

The statement formed by exchanging the hypothesis and conclusion of a conditional statement (q->p)

What is the distance formula?

d = √(x2 - x1)^2 + (y2 - y1)^2

What is a conditional statement?

A logical statement that has a hypothesis and a conclusion (p->q)

Ex: If you are in Houston, then you are in tExas

What is an inverse?

The statement formed by negating both the hypothesis and conclusion of a conditional statement (~p->~q)

What is a negation?

The opposite of a statement

What is a contrapositive?

The statement formed by negating both the hypothesis and conclusion of the converse of a conditional statement (~q->~p)

How do you write a biconditional statement?

When a conditional statement and its converse are both true, you can write them as a single biconditional statement - must contain "if and only if"

What is the midpoint formula?

(x1+x2/2, y1+y2/2)

What is the segment addition postulate?

The segment addition postulate states that if we are given two points on a line segment, A and C, a third point B lies on the line segment AC if and only if the distances between the points meet the requirements of the equation AB + BC = AC.

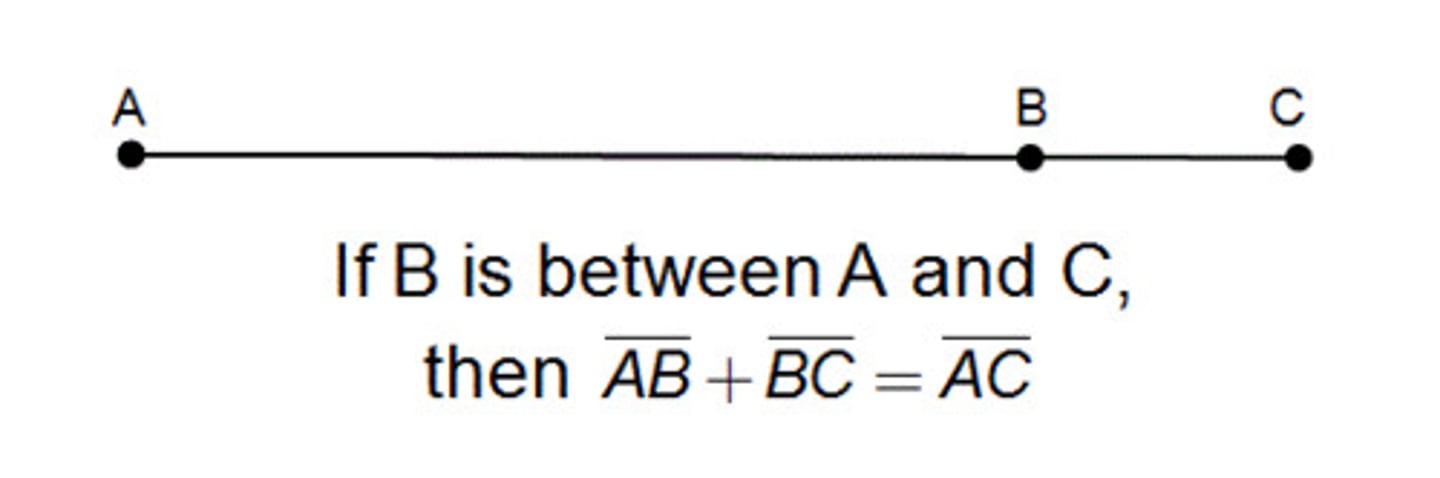
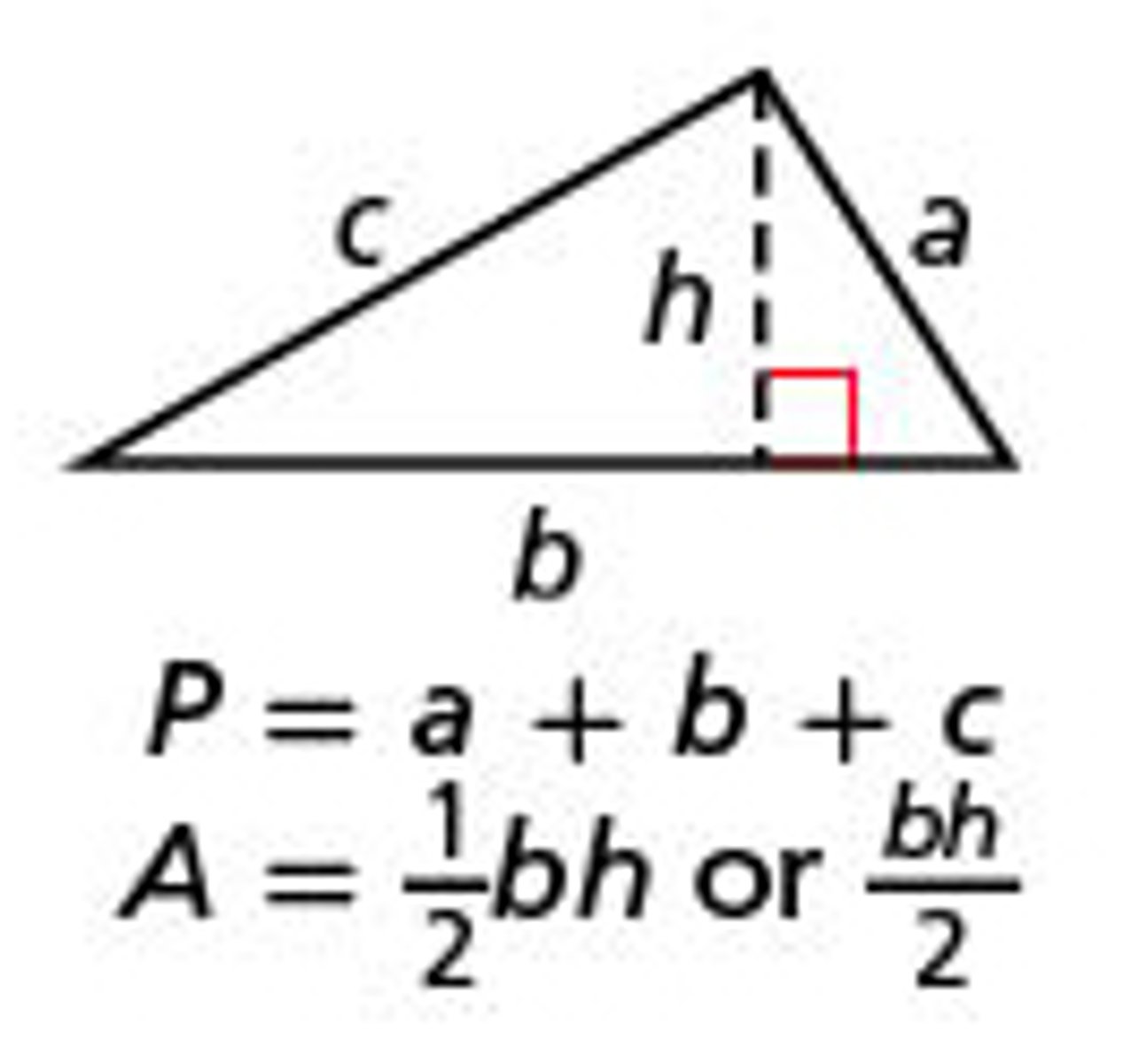
How do you find the perimeter and area of a triangle?

P = a + b + c

A = 1/2bh

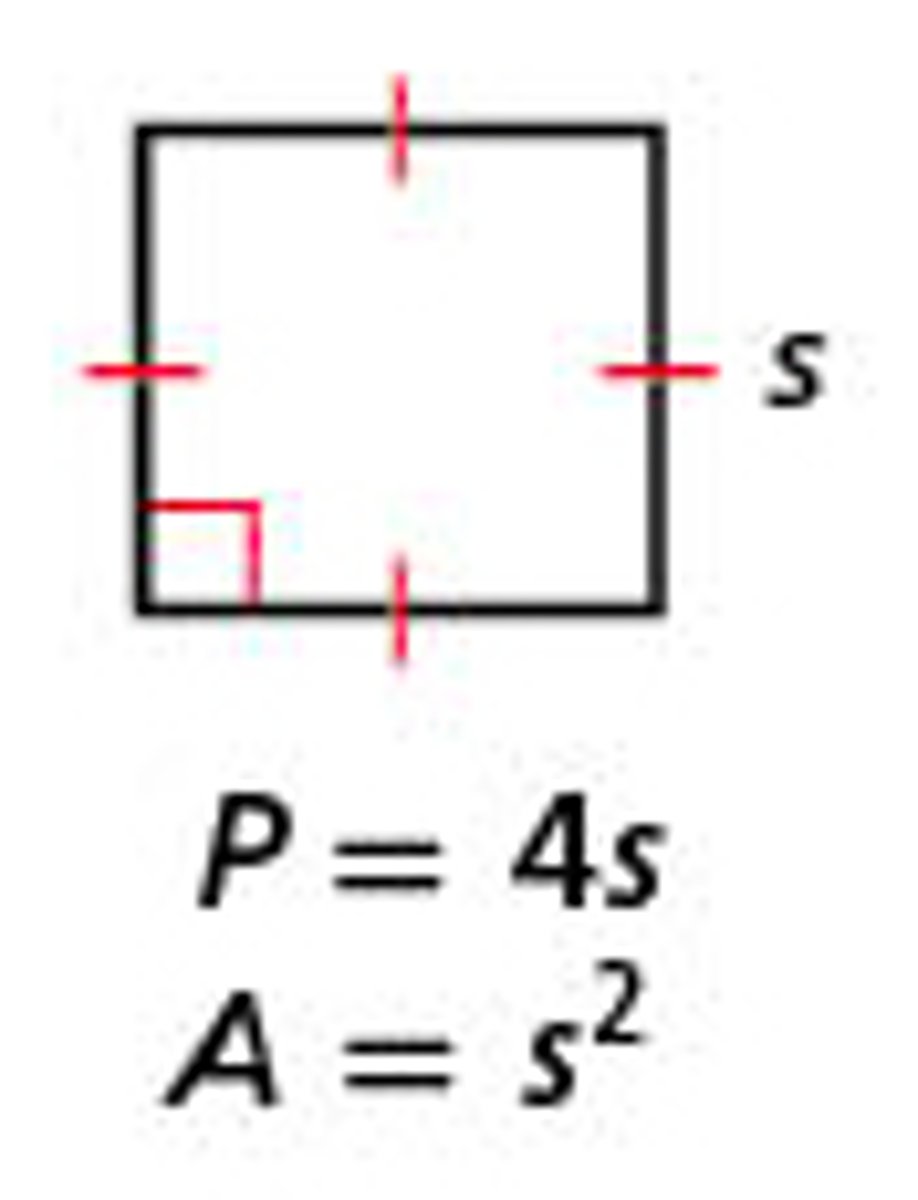
How do you find the perimeter and area of a square?

P = 4s

A = s^2

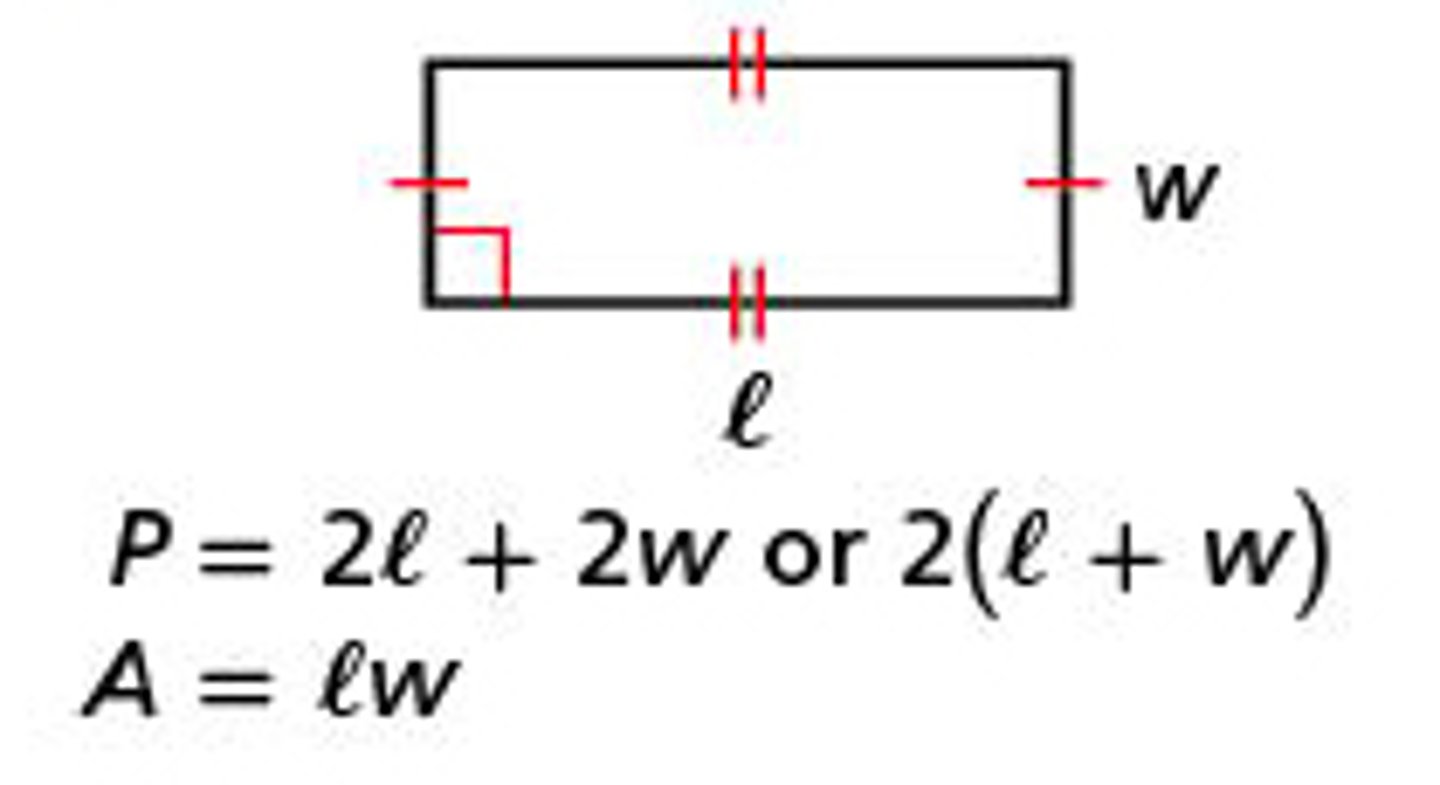
How do you find the perimeter and area of a rectangle?

P = 2l + 2w

A = lw

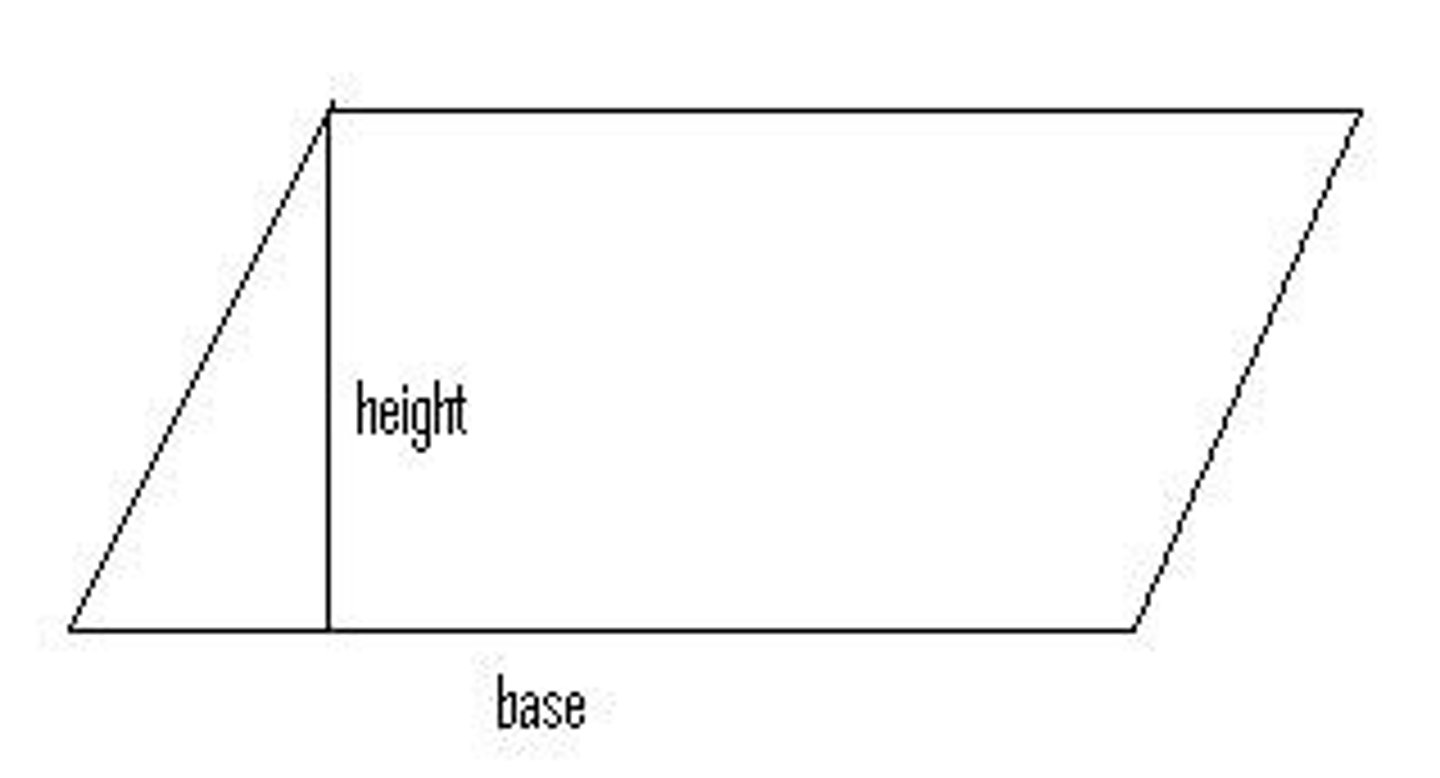
How do you find the area of a parallelogram?

A = bh

What is a conjecture?

An unproven statement that is based on observations

What is a counterexample?

A specific case for which a conjecture is false

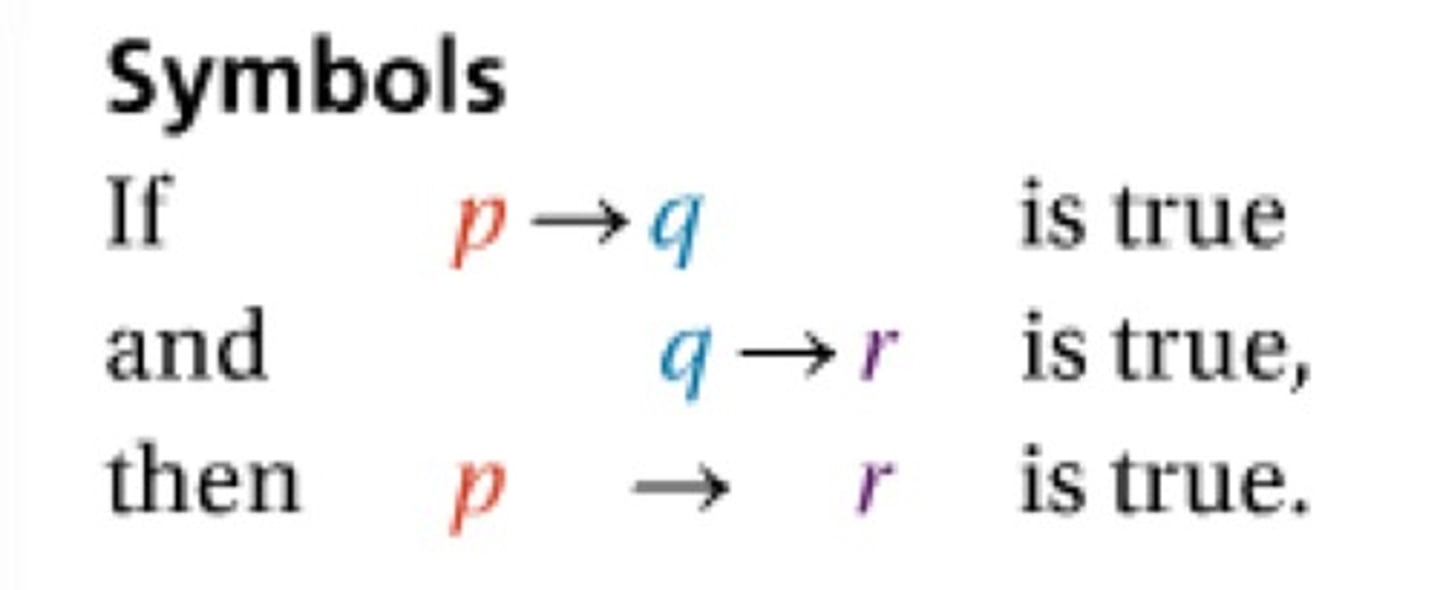
What is the Law of Syllogism?

If the hypothesis p, then conclusion q

If that statement is true then

If hypothesis q, then conclusion r

If hypothesis p, then conclusion r

Then that statements are true

What is the Law of Detachment?

if the hypothesis of a true conditional statement is true, then the conclusion is also true

What is the inductive and deductive reasoning?

Inductive - Based on observations

Deductive - Uses fasts, definitions, laws of logic, etc

What is the reflexive property?

A = A

What is the symmetric property?

If a= b, then b = a

What is the transitive property?

If a = b and b = c, then a = c

What is the right angles congruence theorem?

All right angles are congruent

What is the congruent supplements theorem?

If two angles are supplementary to the same angle, then they are congruent

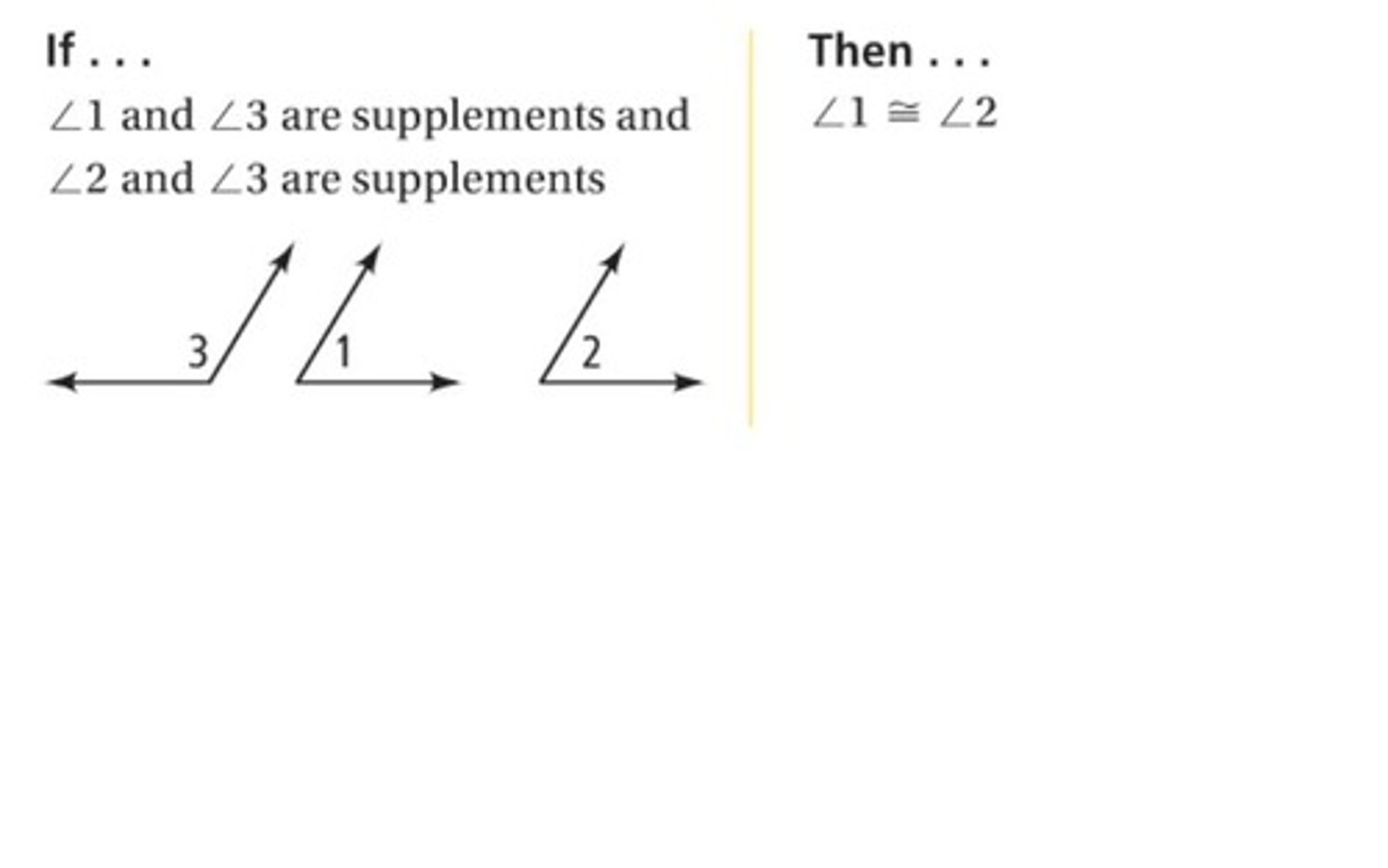
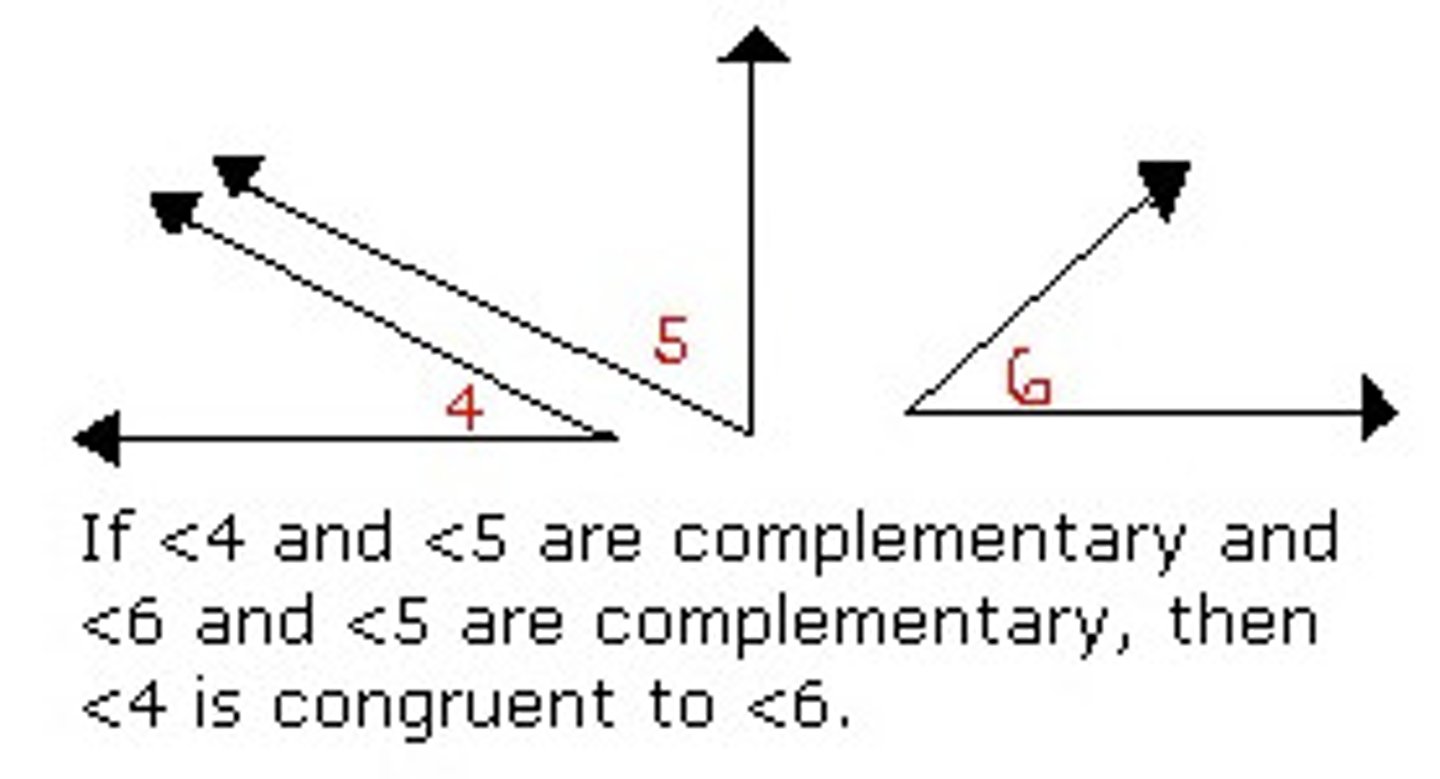
What is the congruent complements theorem?

If two angles are complementary to the same angle, then they are congruent

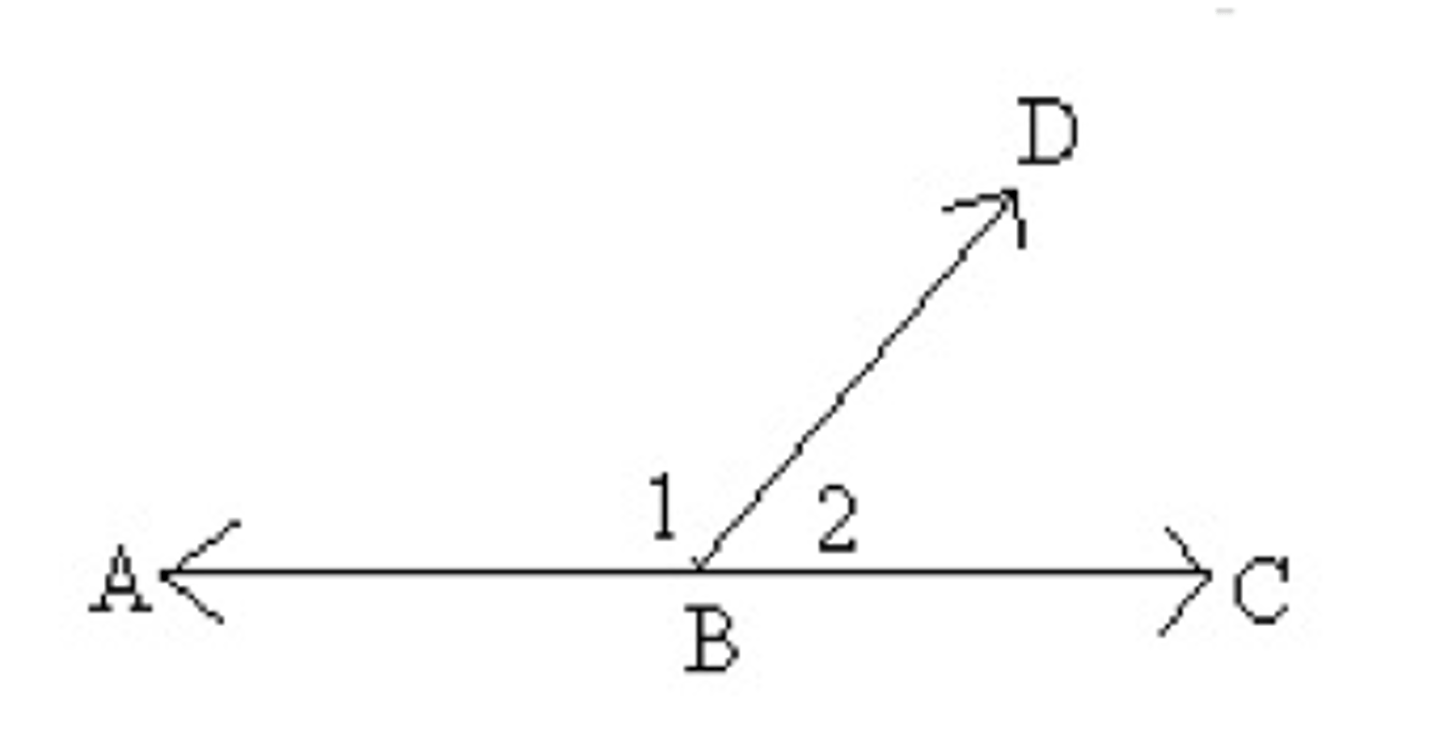
What is the linear pair postulate?

If two angles form a linear pair, then they are supplementary

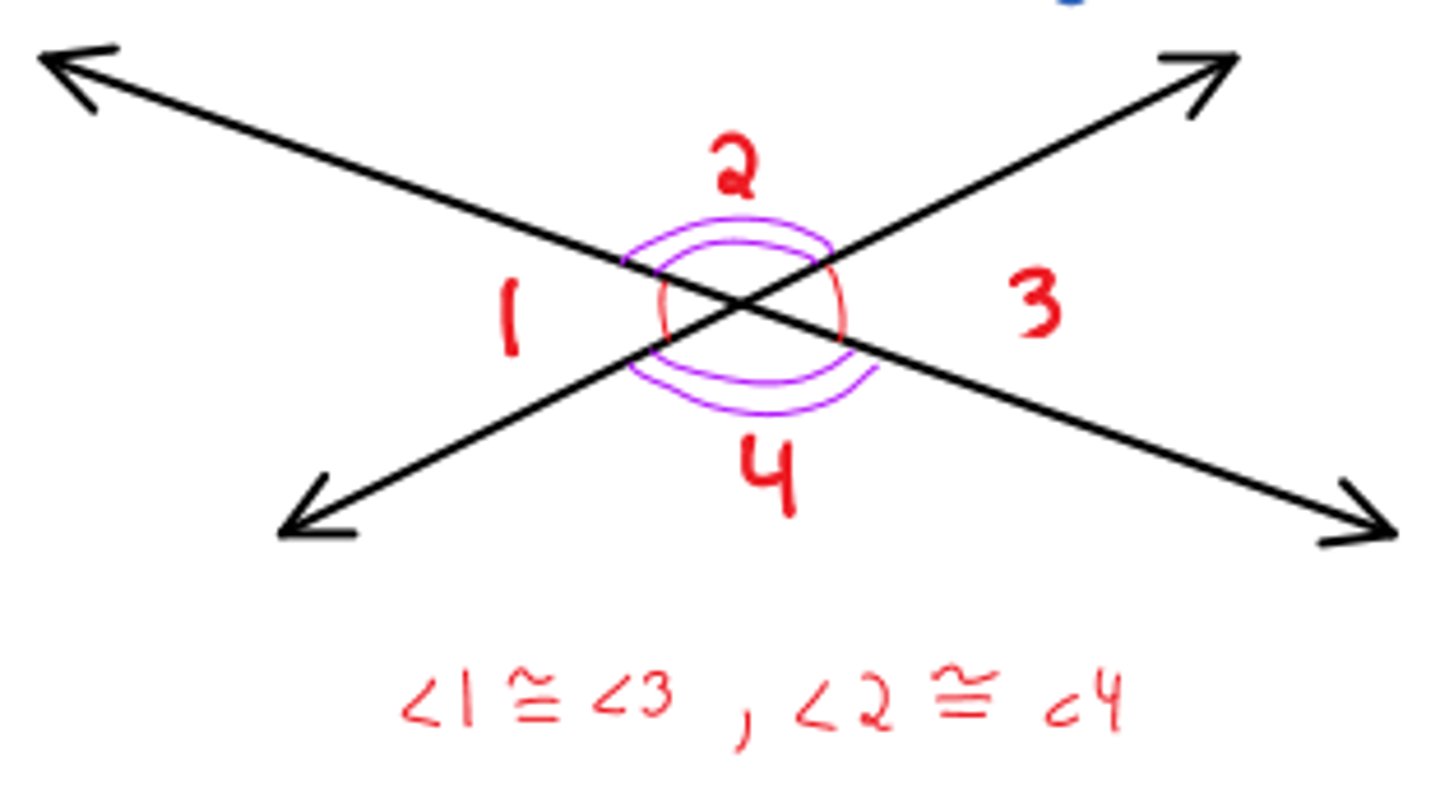
What is the vertical angles congruence theorem?

Vertical angles are congruent

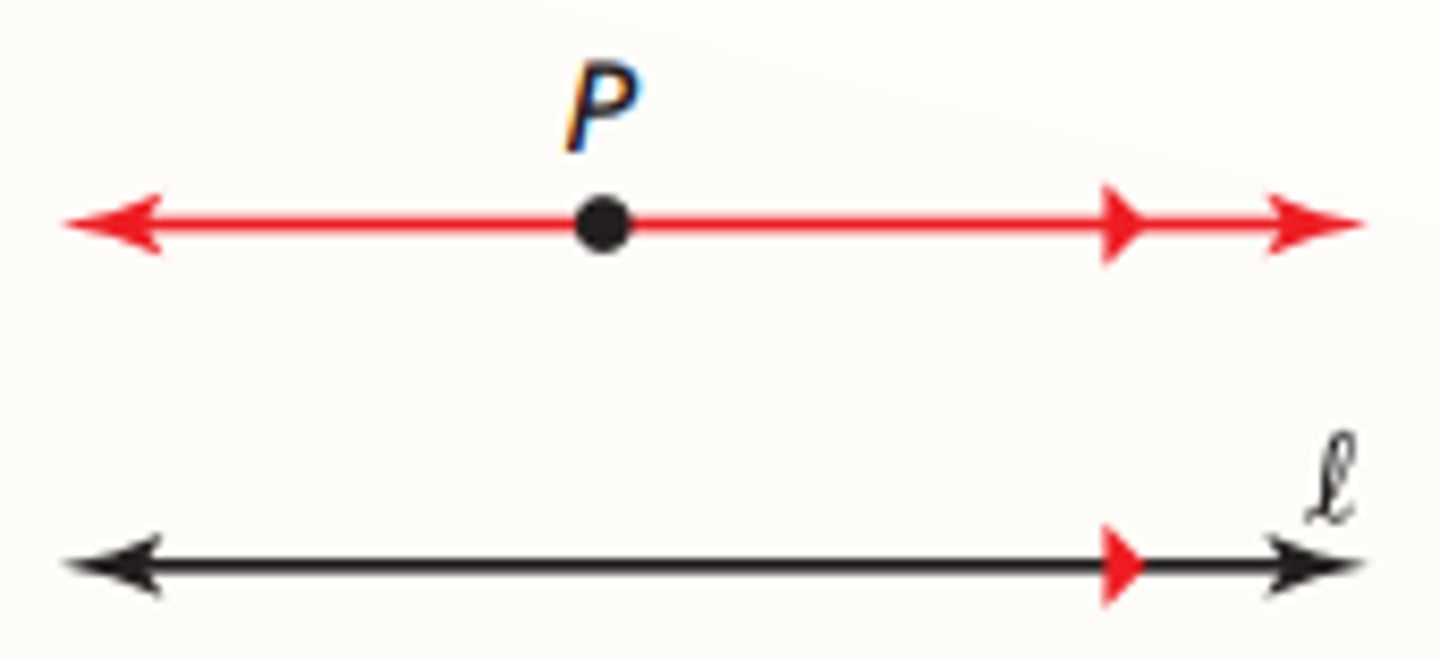
What is the parallel postulate?

If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line

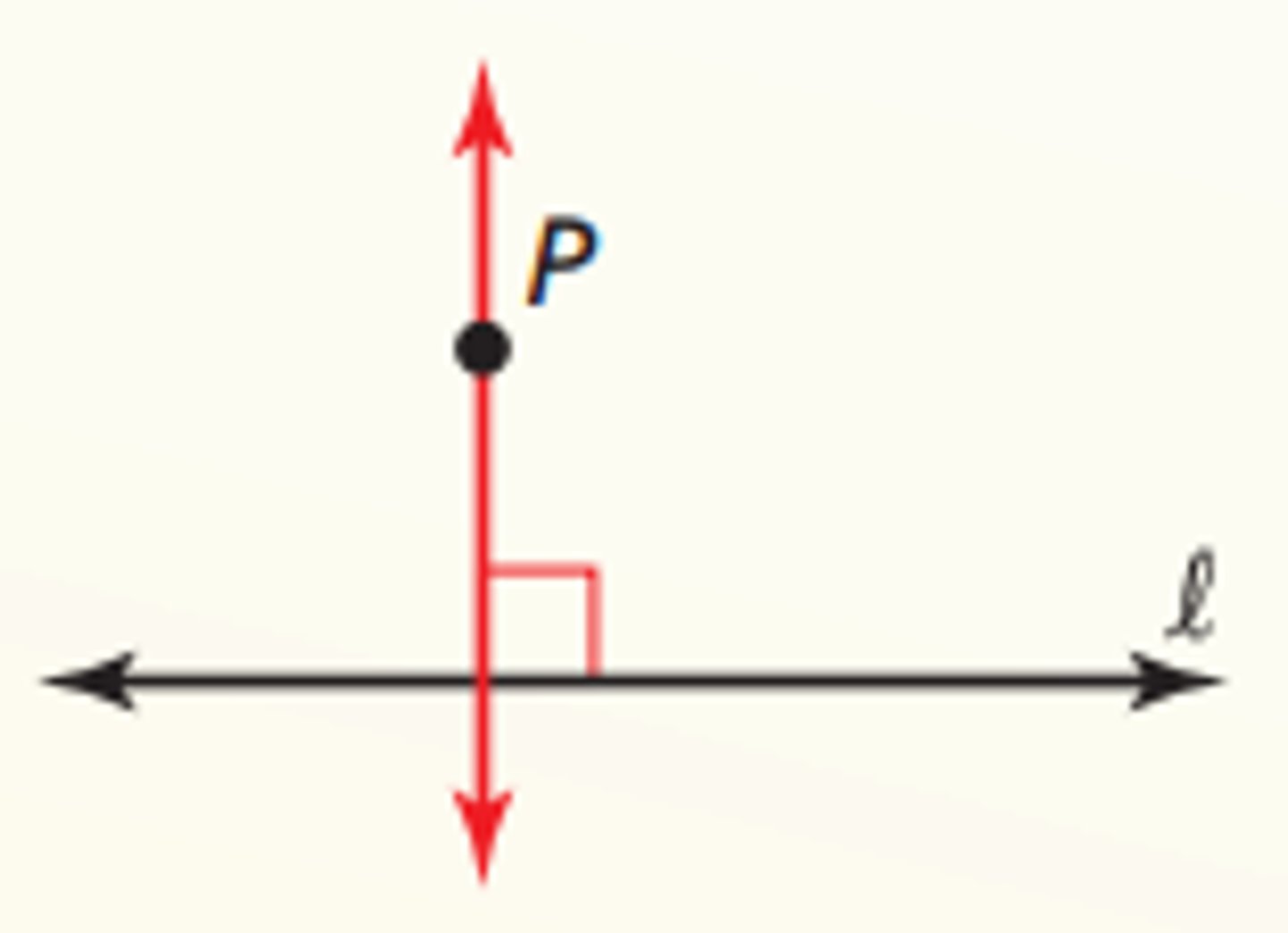
What is the perpendicular postulate?

If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line

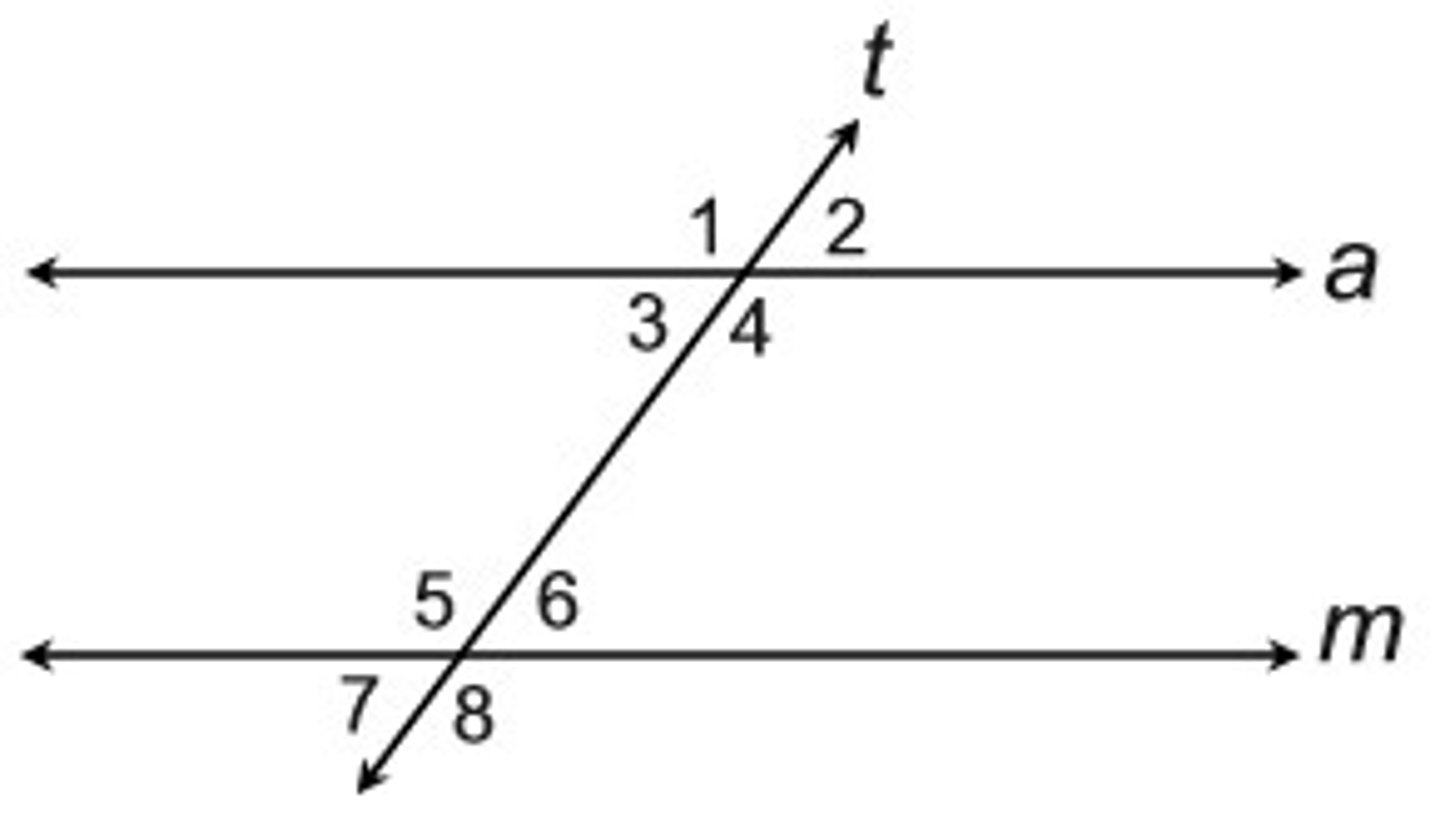
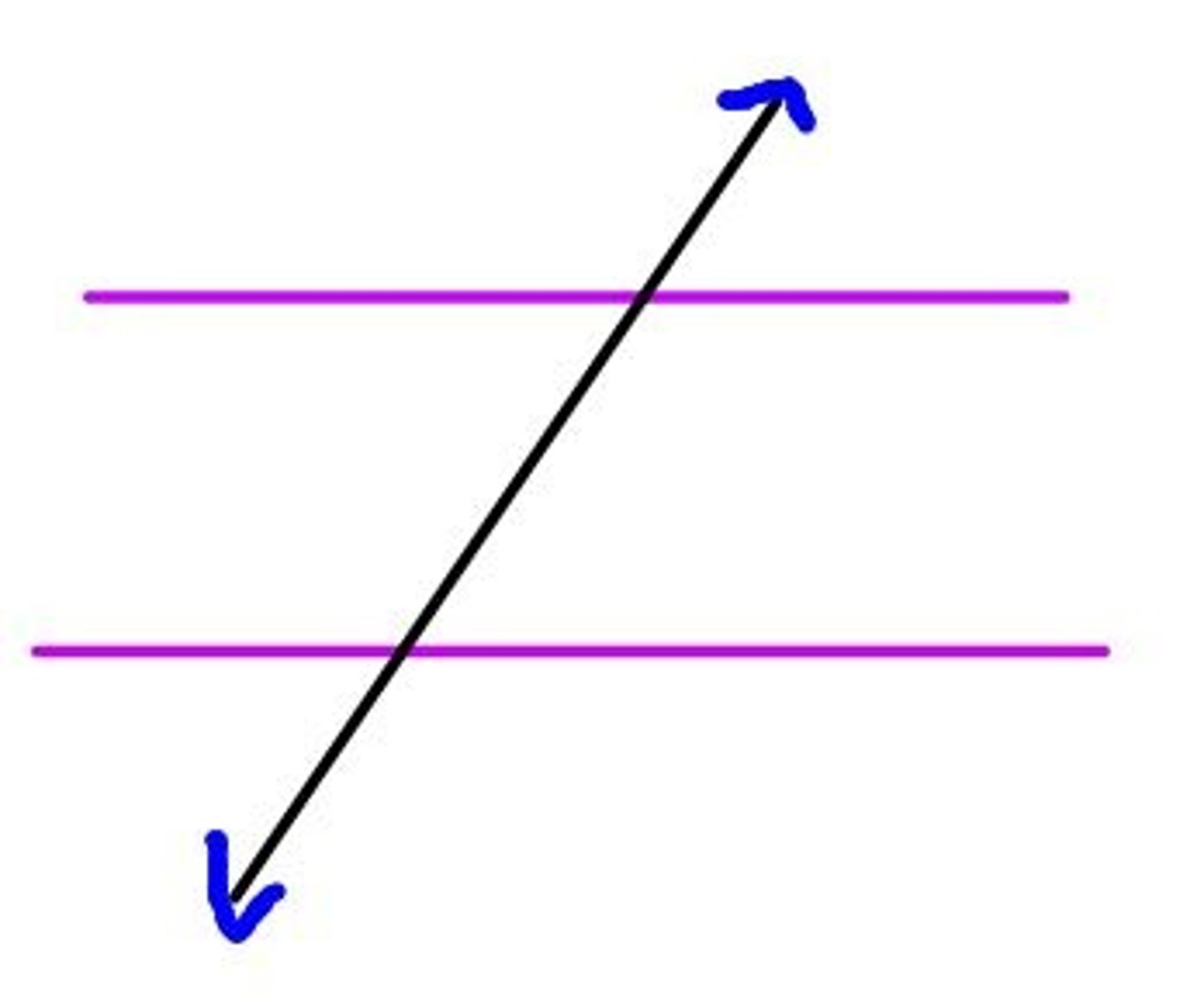
What is a transversal?

A line that intersects two or more coplanar lines at different points

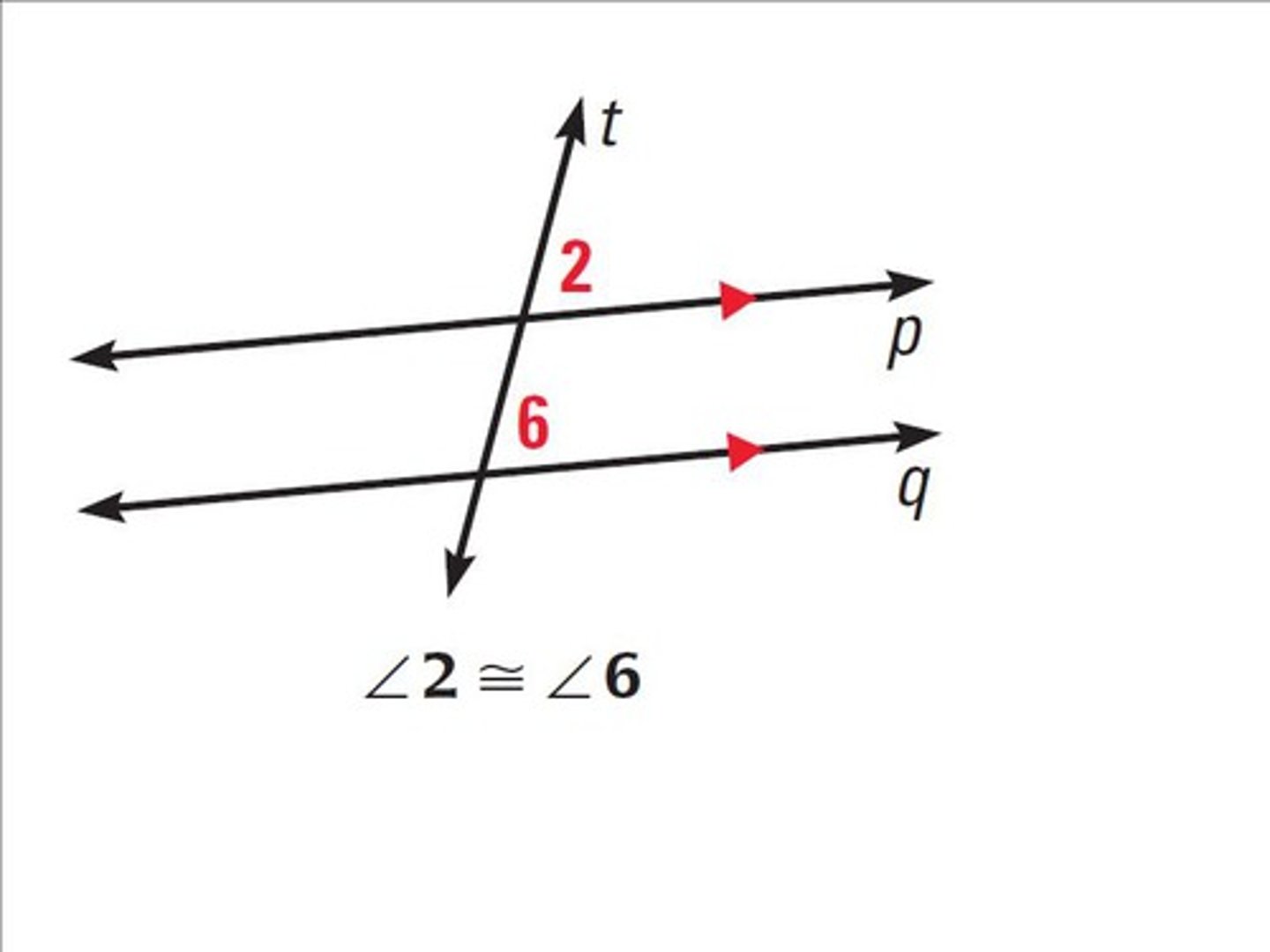
What is the corresponding angles theorem?

If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent

What is the alternate interior angles theorem?

If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent

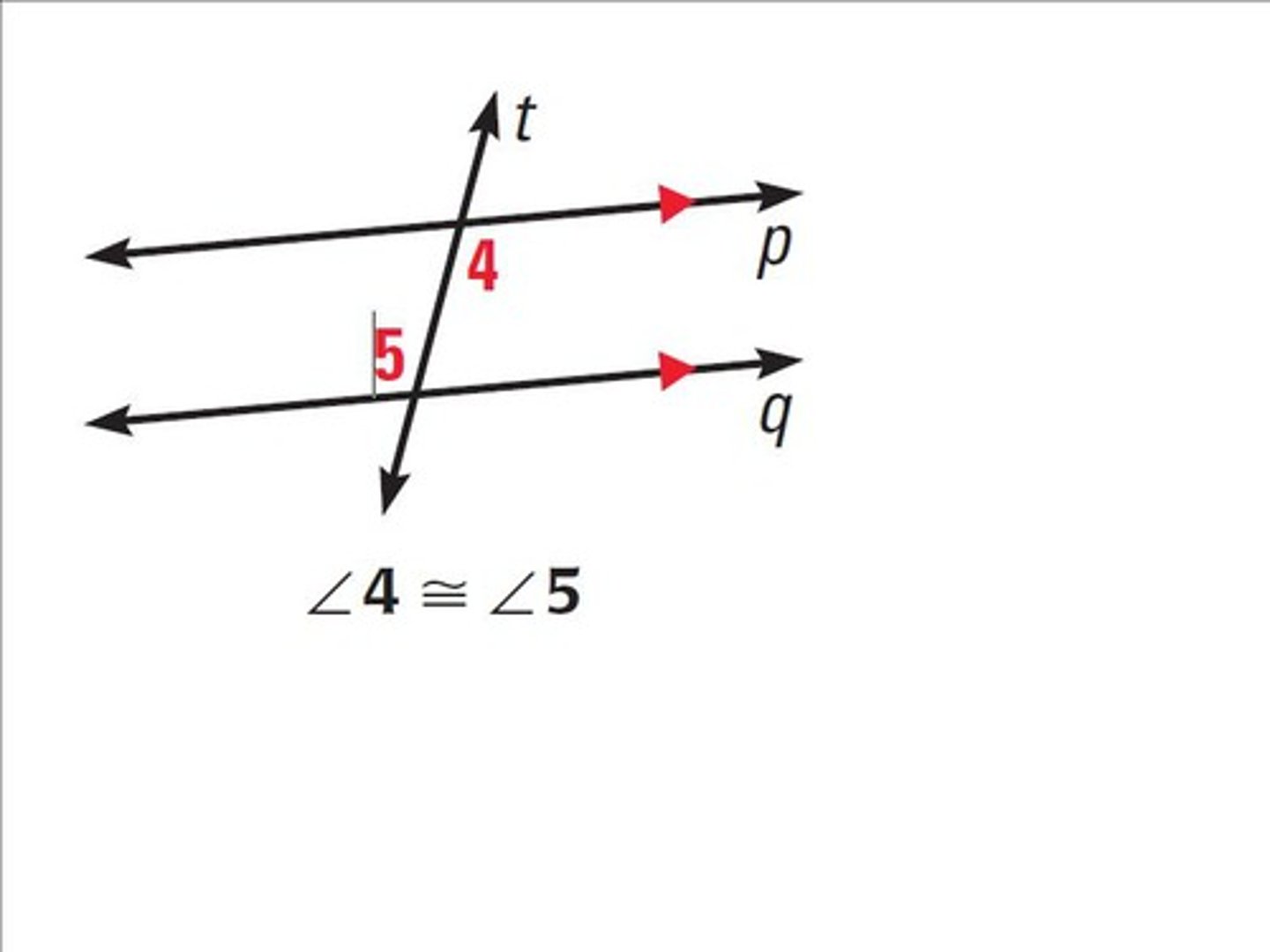
What is the alternate exterior angles theorem?

If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent

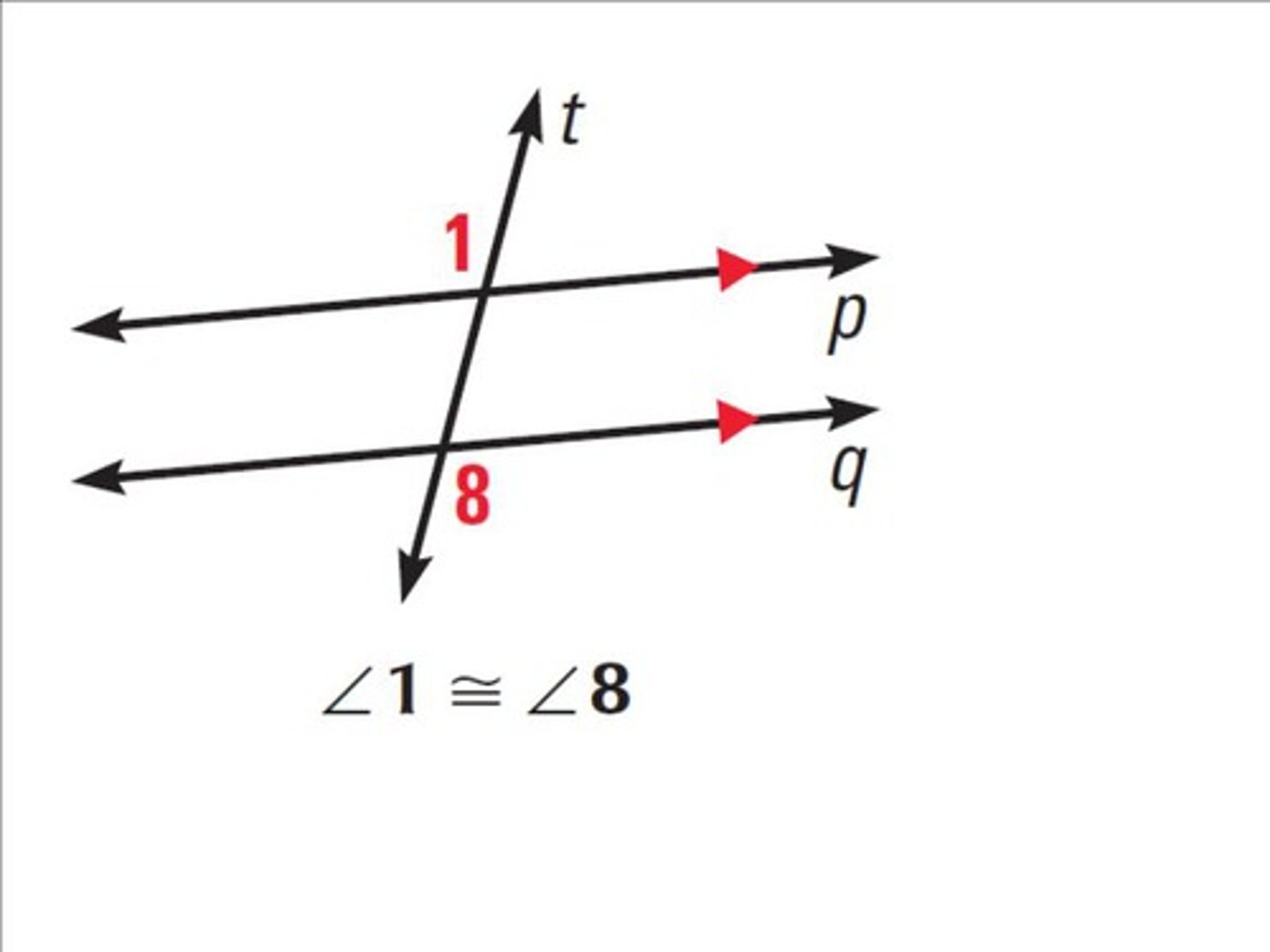
What is the consecutive interior angles theorem?

If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary

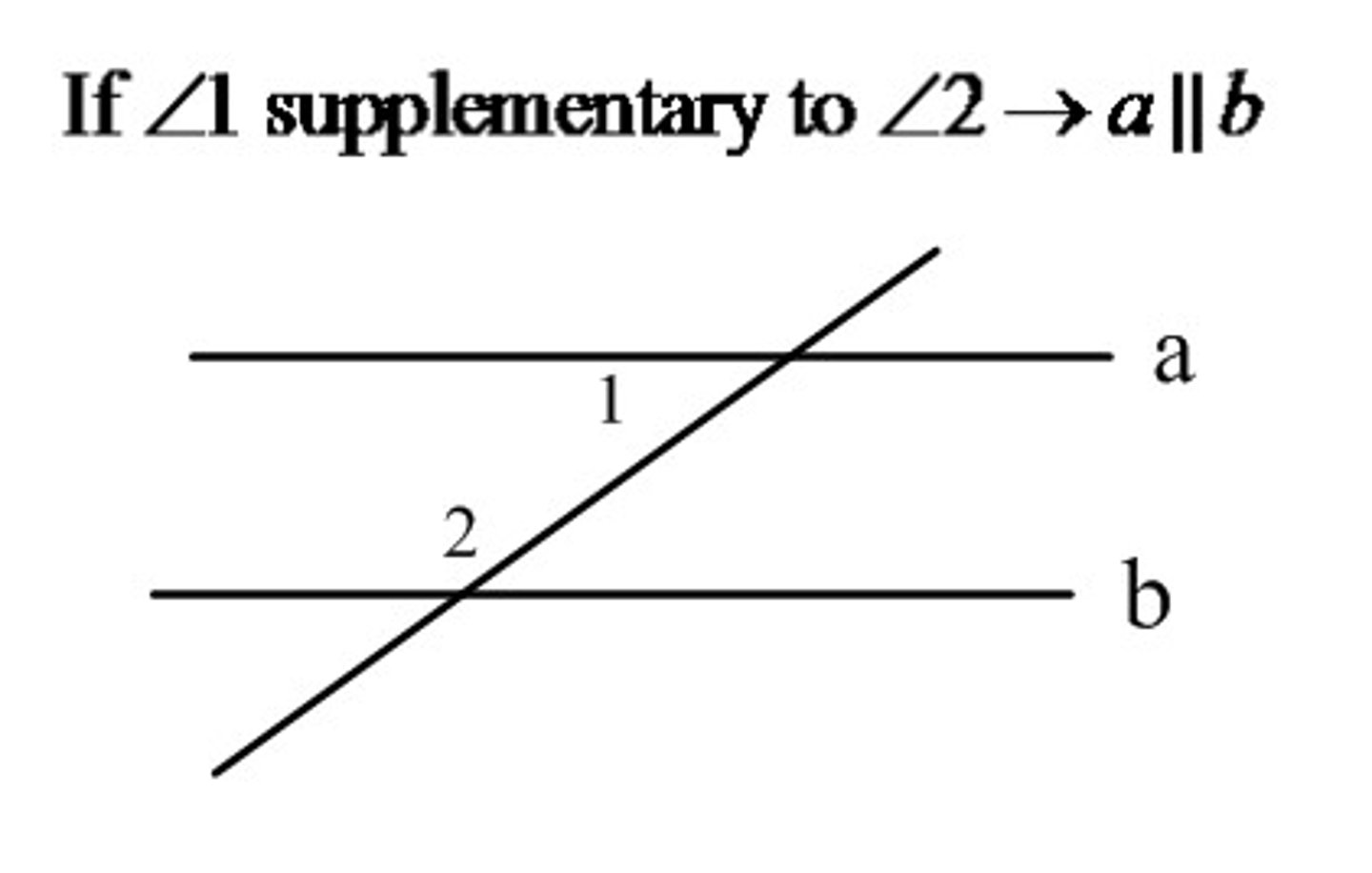
What is the corresponding angles converse?

If two lines are cut by a transversal so the corresponding angles are congruent, then the lines are parallel

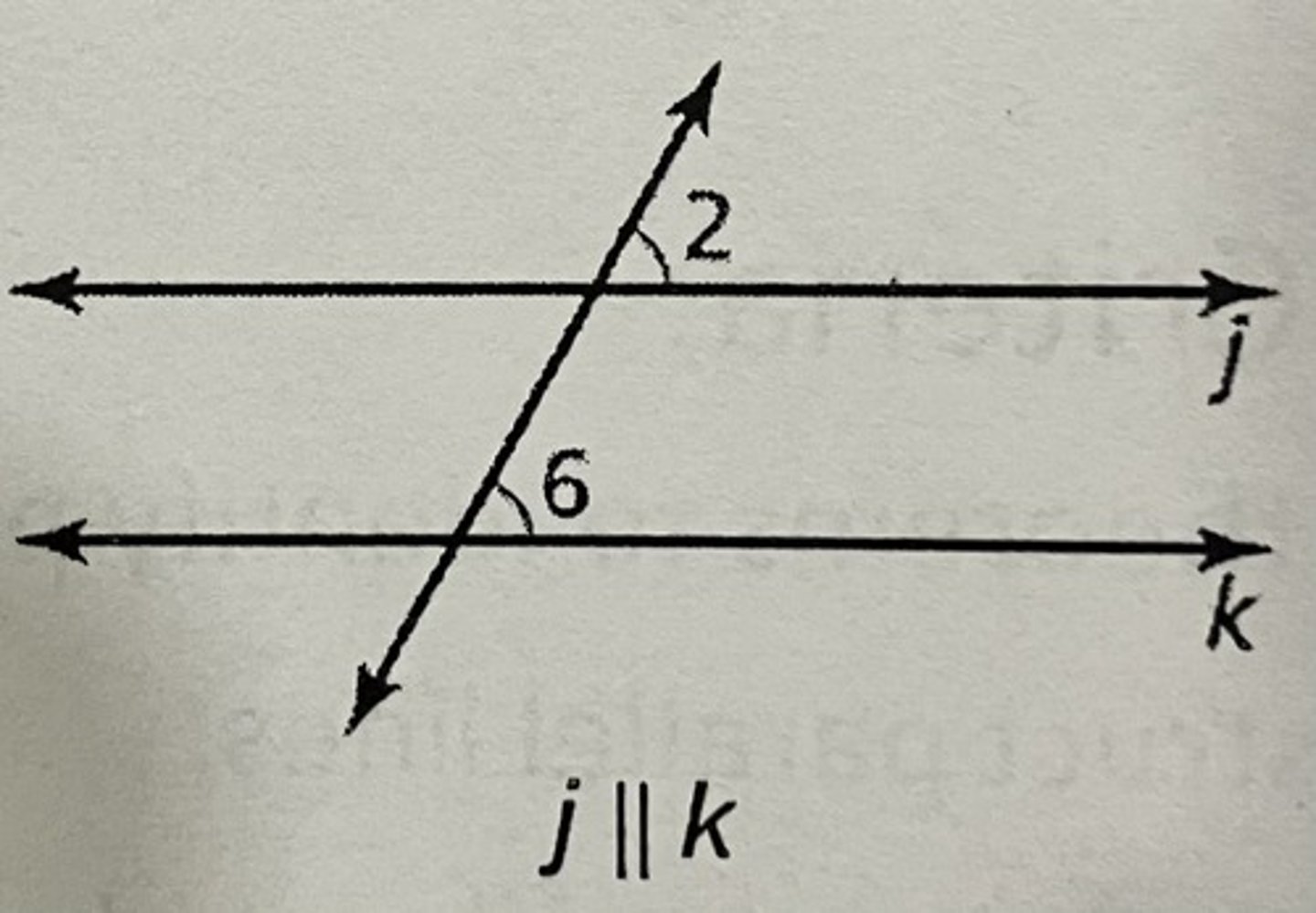
What is the alternate interior angles converse?

If two lines are cut by a transversal so the alternate interior angles are congruent, then the lines are parallel

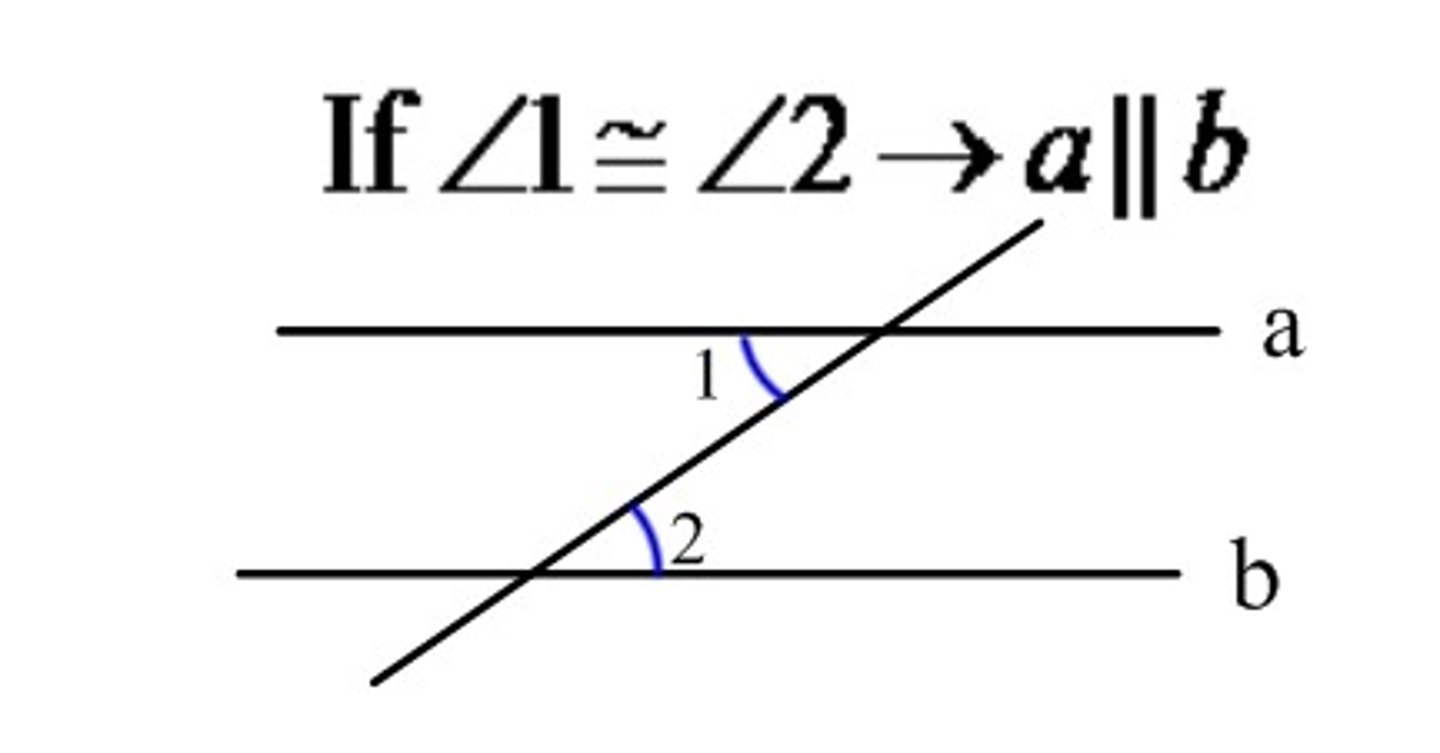
What is the alternate exterior angles converse?

If two lines are cut by a transversal so the alternate exterior angles are congruent, then the lines are parallel

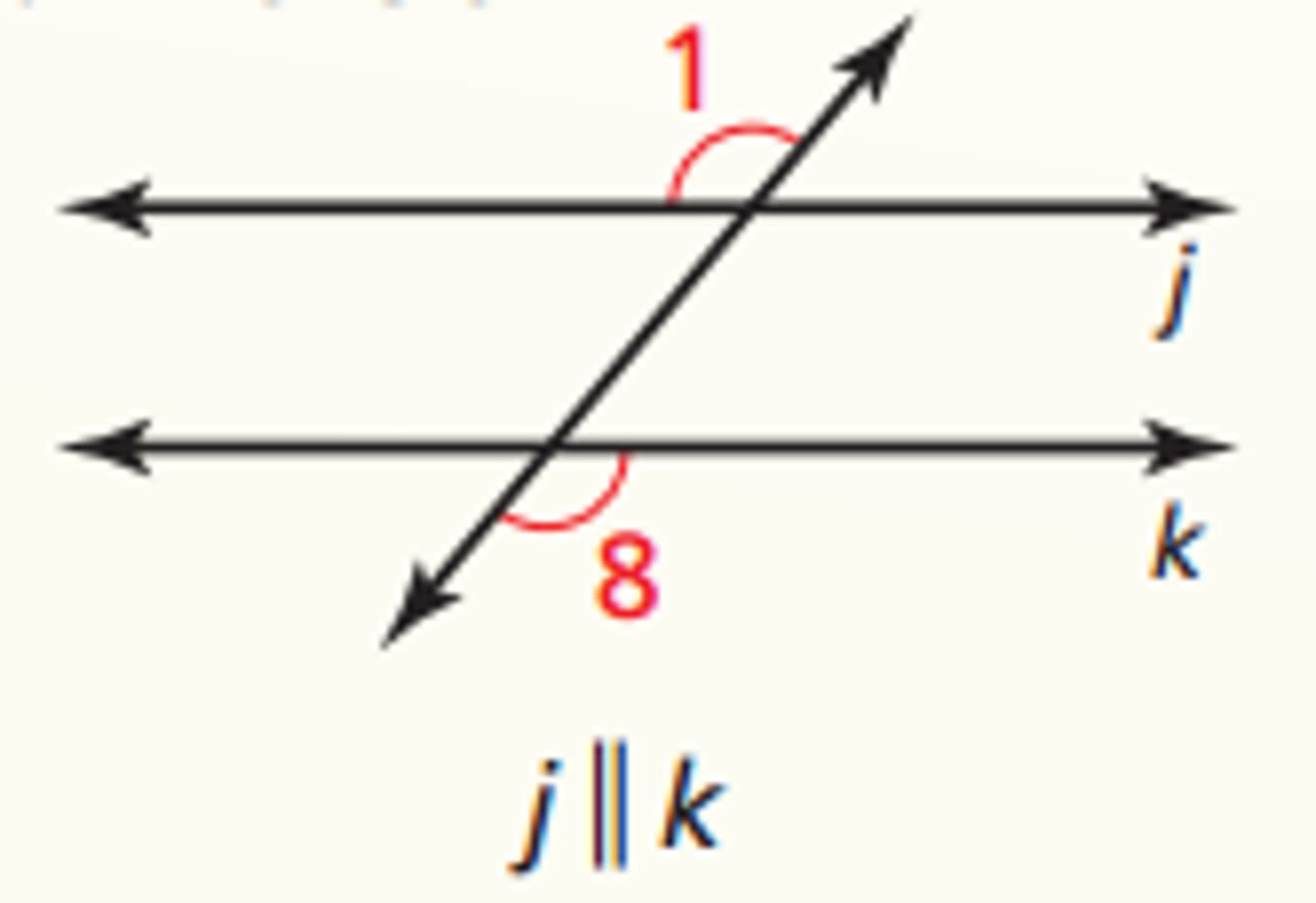
What is the consecutive interior angles converse?

If two lines are cut by a transversal so the consecutive interior angles are supplementary, then the lines are parallel

How do you find the distance from a point to a line?

You use the distance formula

What is the transitive property of parallel lines?

If two lines are parallel to the same line, then they are parallel to each other

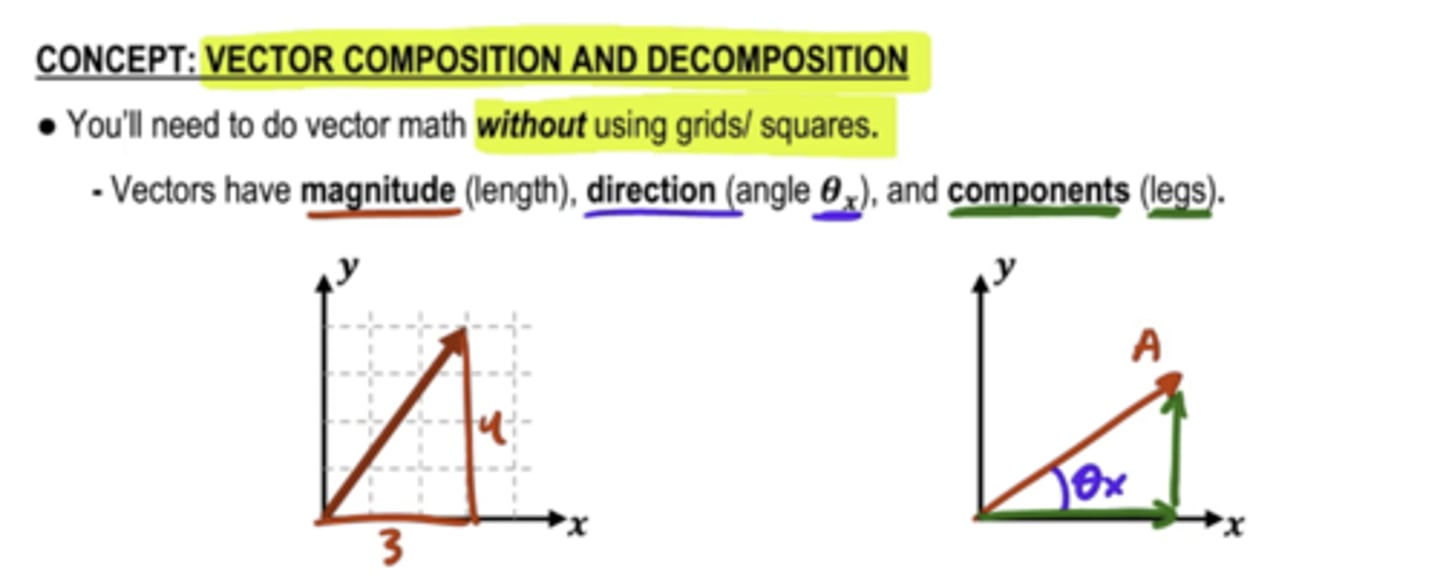
How do you write a vector?

The initial point to the terminal point

<3,4>

What is the translation postulate?

A translation is a rigid motion

How do you know if lines are perpendicular and parallel?

If their slopes are reciprocals or the same exact

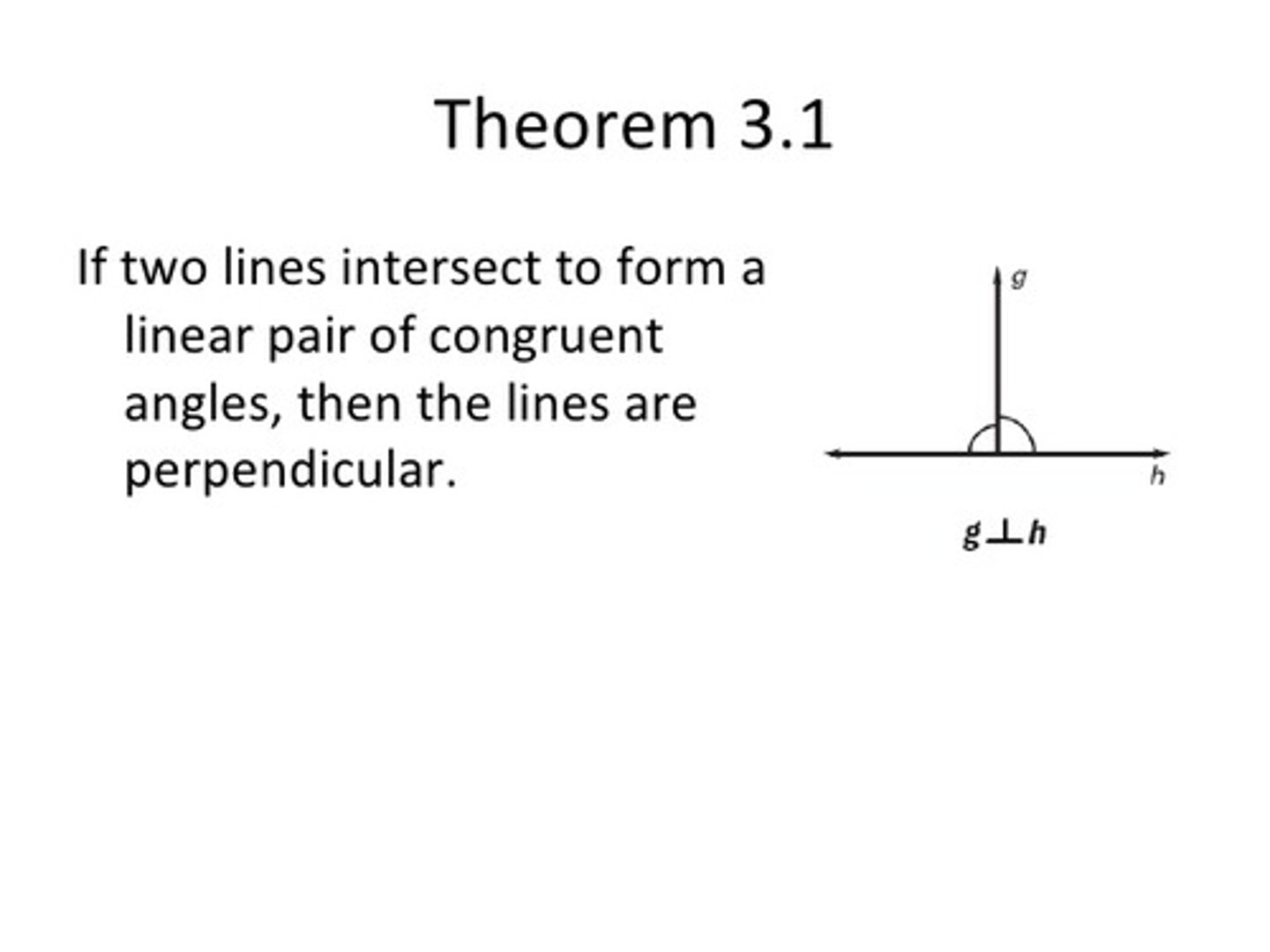
What is the line pair perpendicular theorem?

If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular

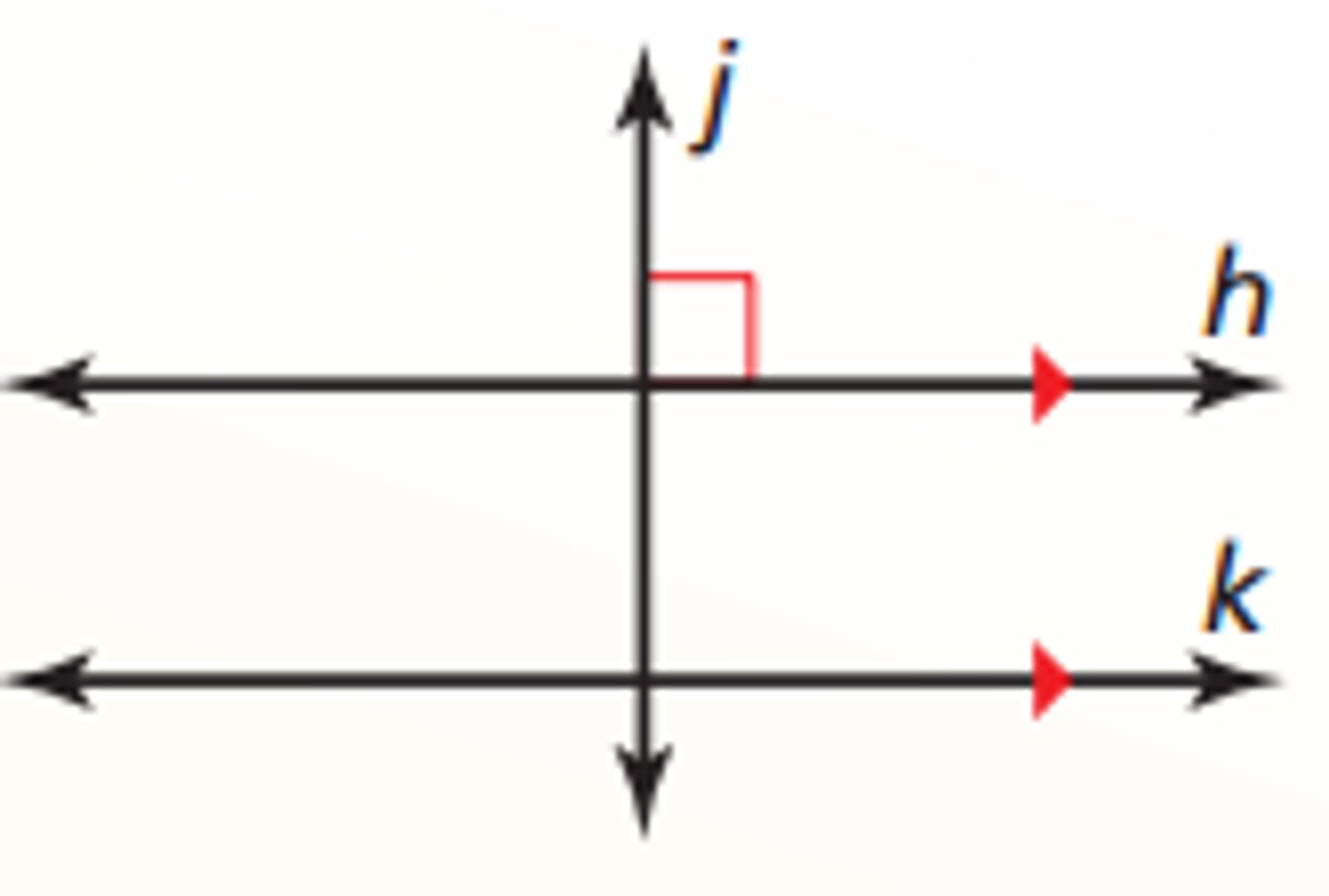
What is the perpendicular transversal theorem?

In a plane, if a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line

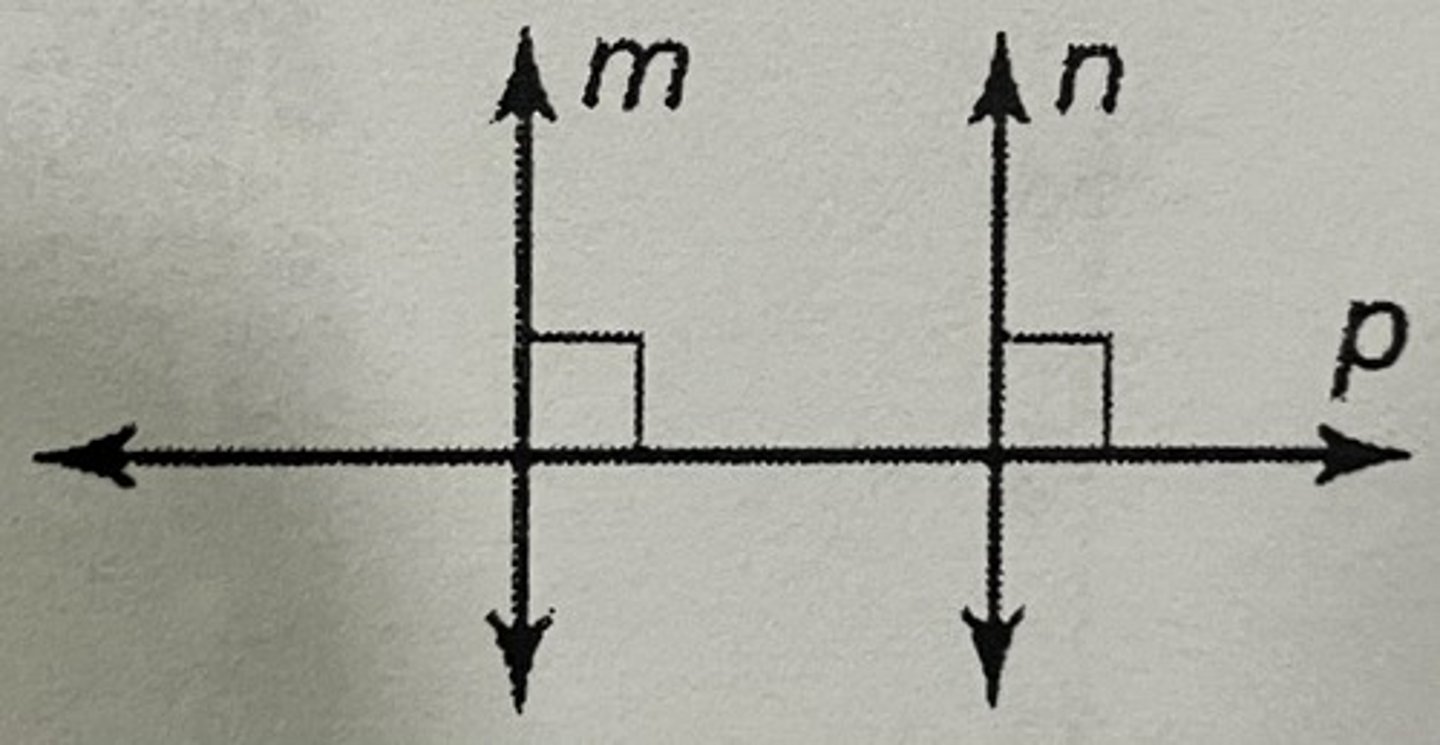
What is the lines perpendicular to a transversal theorem?

In a plane, if two lines are perpendicular to the same line, then they are parallel to each other

If (a,b) is reflected in the x-axis then its image is the point...

(a,-b)

If (a,b) is reflected in the y-axis then its image is the point...

(-a,b)

If (a,b) is reflected in the line y = x then its image is the point...

(b,a)

If (a,b) is reflected in the line y = -x then its image is the point...

(-b,-a)

What is a glide reflection?

A transformation involving a translation followed by a reflection

What is the composition theorem?

The composition of two (or more) rigid motions is a rigid motion

What is a translation?

It moves every point of a figure the same distance and direction

What is the point rotation of 90 degrees?

(-b,a)

What is the point rotation of 180 degrees?

(-a,-b)

What is the point rotation of 270 degrees?

(b,-a)

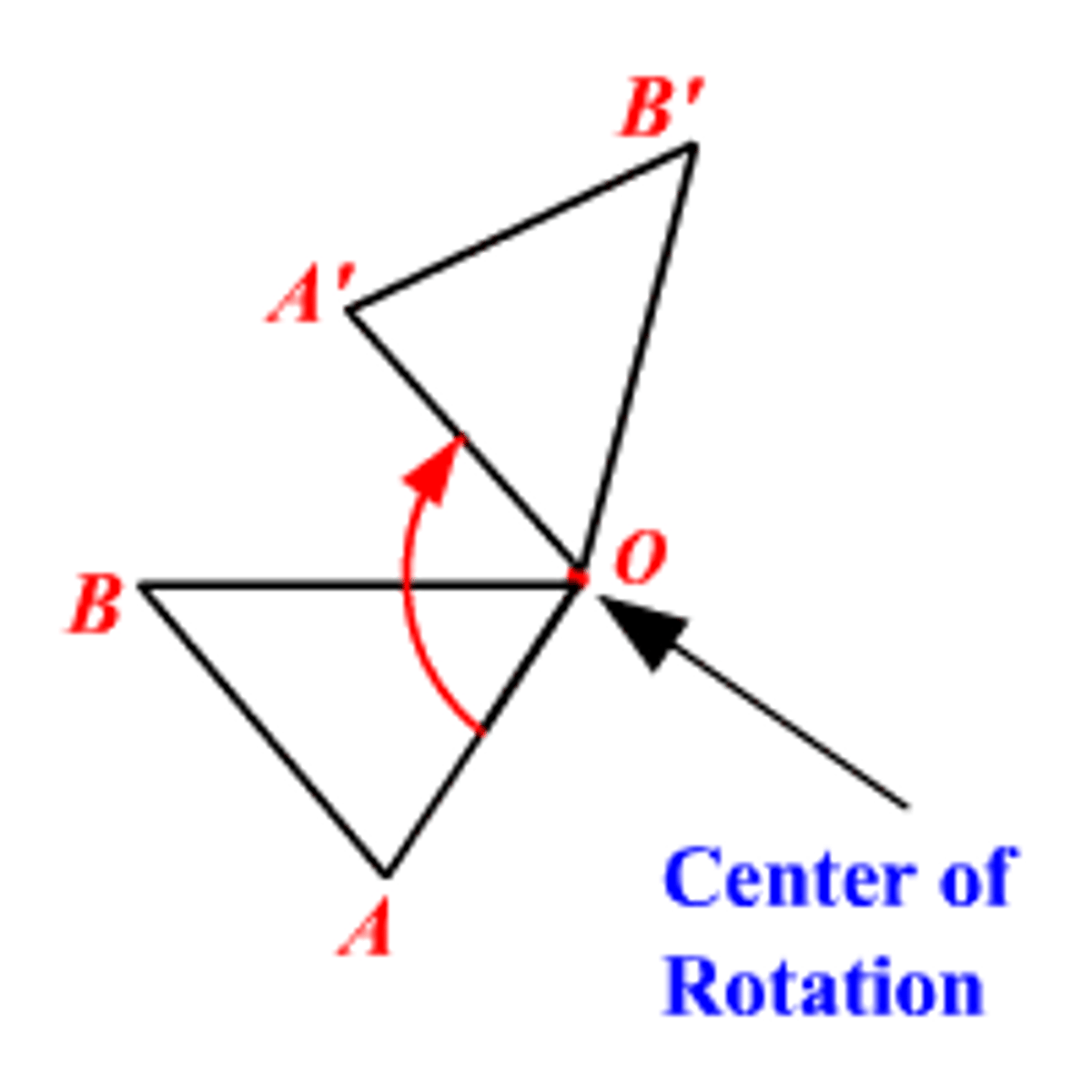
What is the center of rotation?

The fixed point of rotation

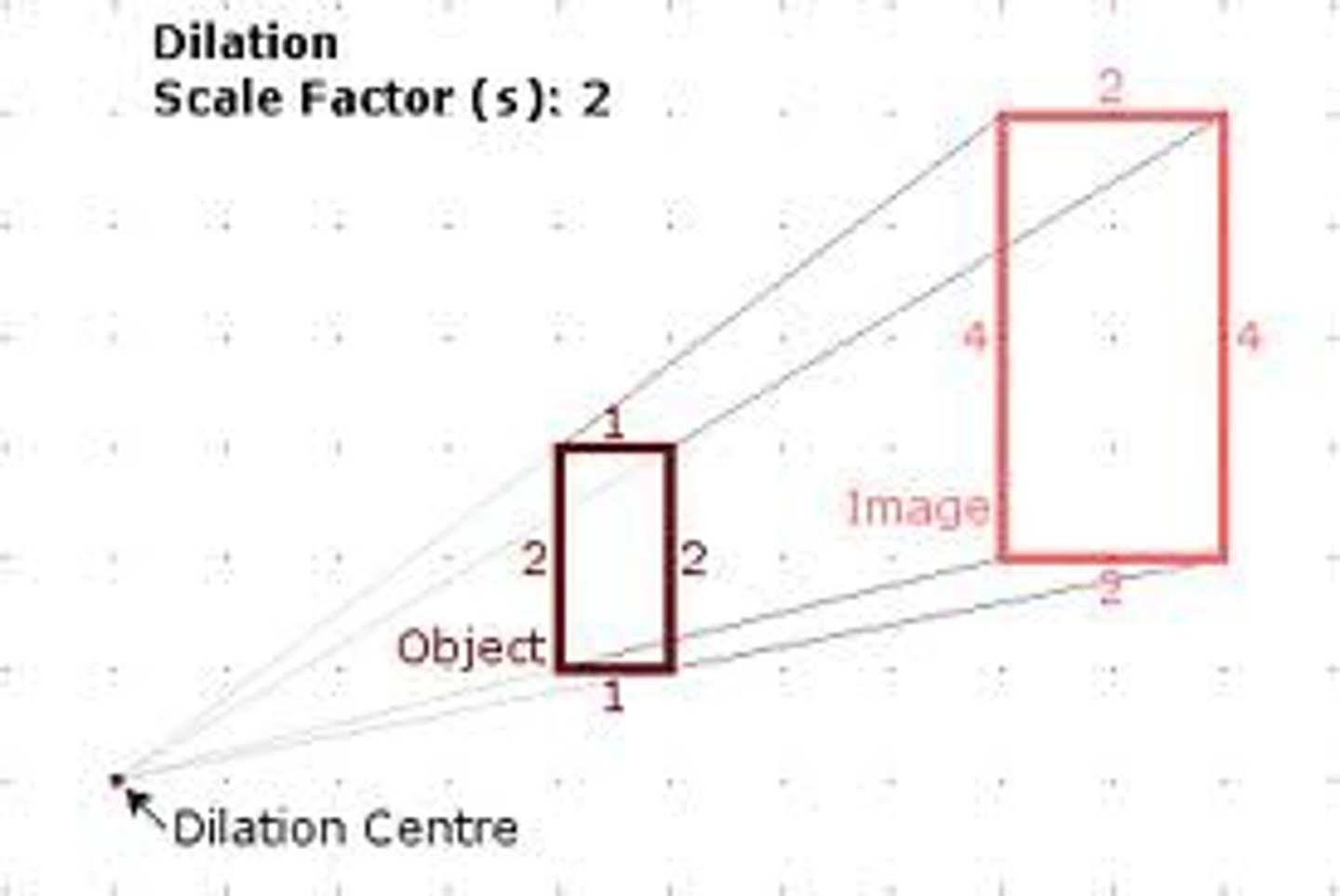
What is a dilation?

A transformation in which a figure is enlarged or reduced with respect to a fixed point C called the center of dilation and a scale factor

What is the scale factor?

The ratio of the lengths of the corresponding sides of the image and the preimage of a dilation

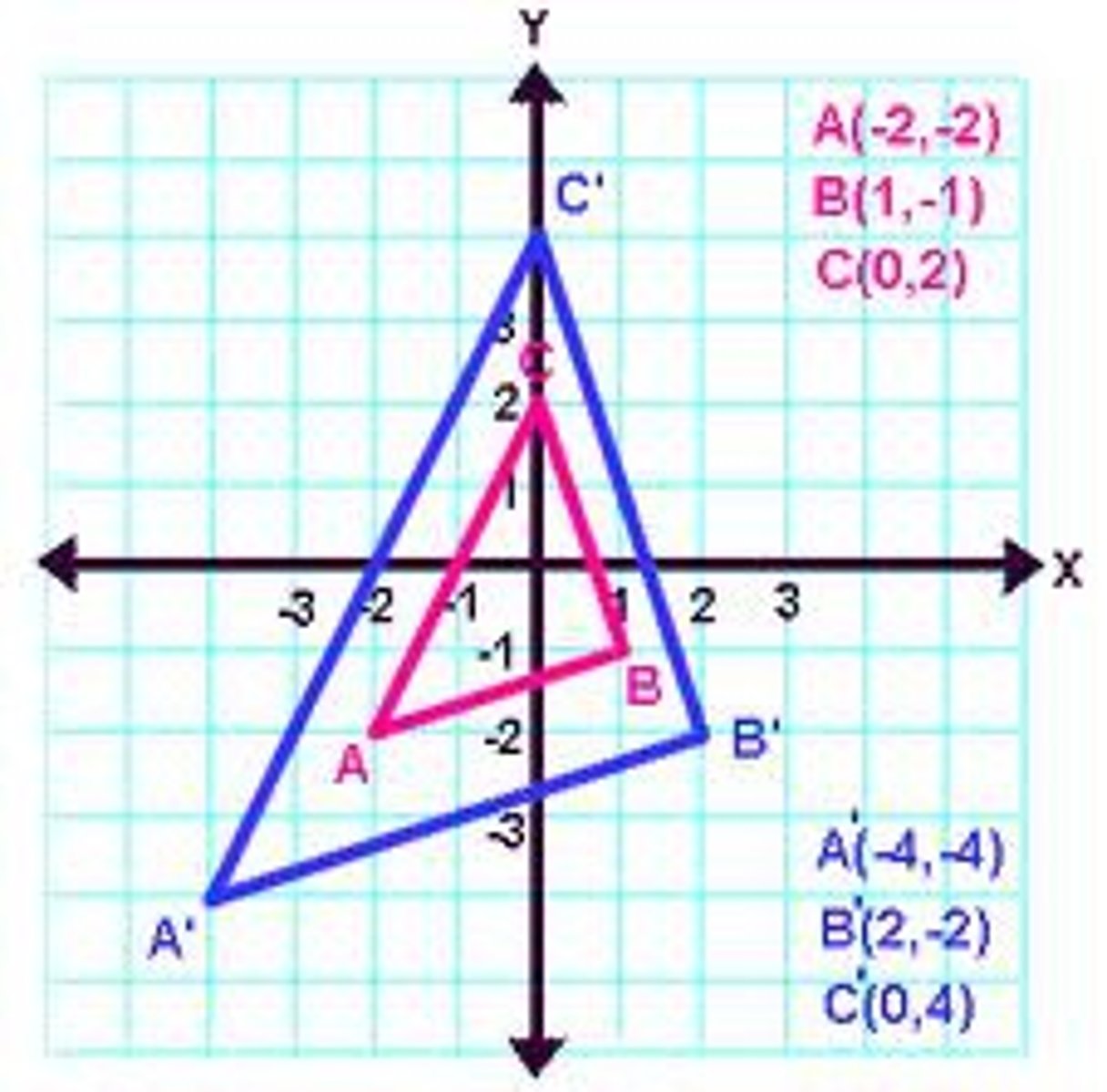
What is the difference between preimage and image?

The preimage is drawn first then the image

How do you label a image?

You label the angles with a '

Example: P' (angle P of the image)

What is an enlargement and reduction?

Enlargement - a dilation in which the scale factor is greater than one

Reduction - a dilation in which the scale factor is greater than zero and less than one

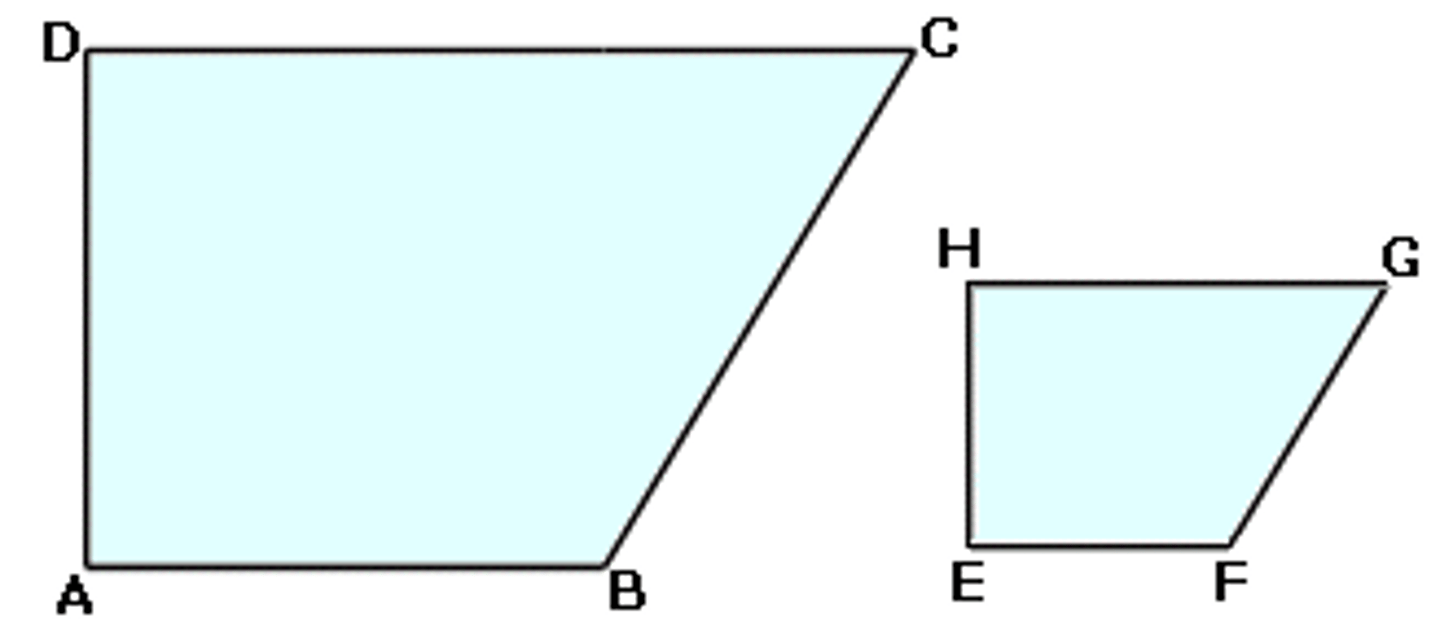
What is a similarity transformation?

A dilation or a composition of rigid motions and dilation

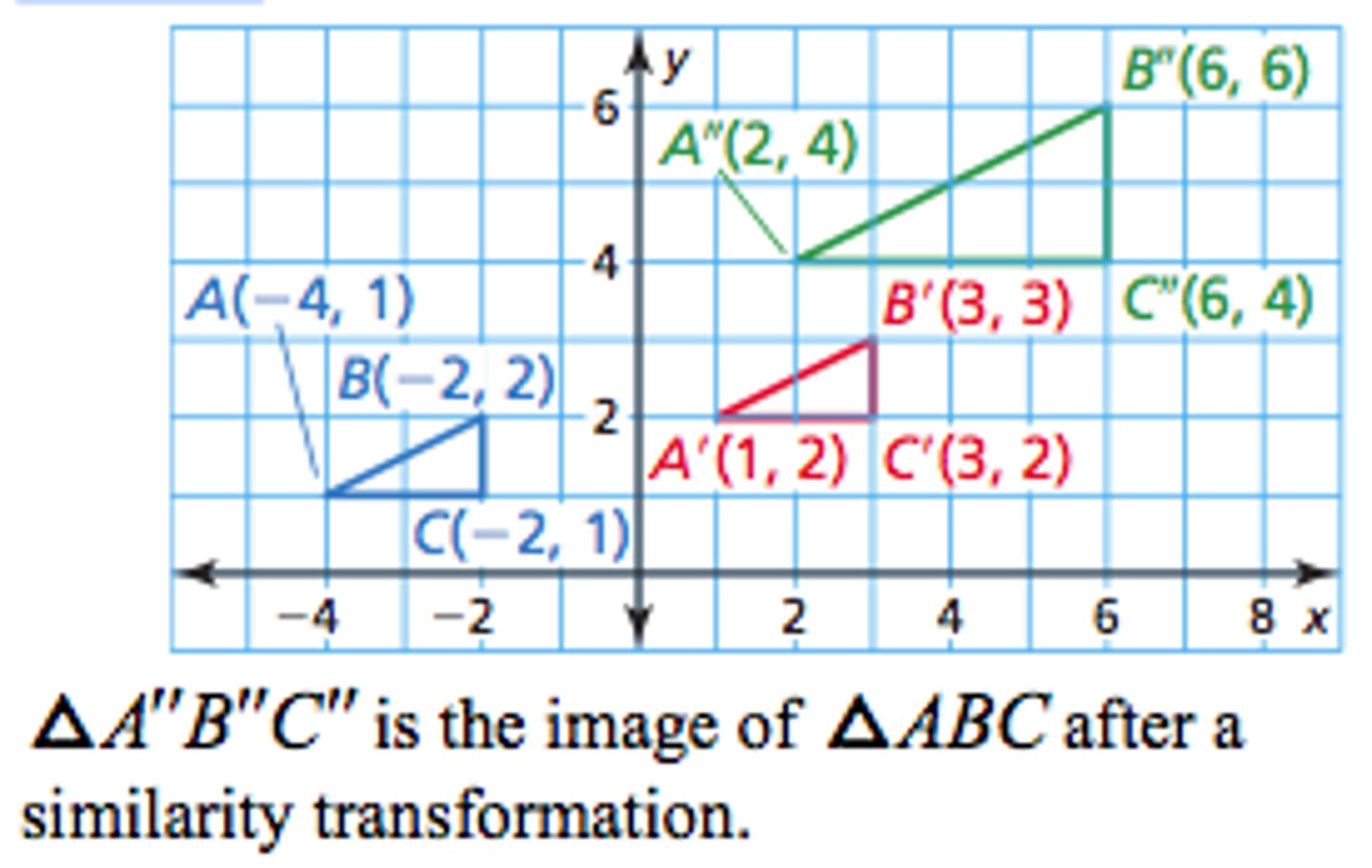
What are similar figures?

Geometric figures that have the same shape, but not necessarily the same size

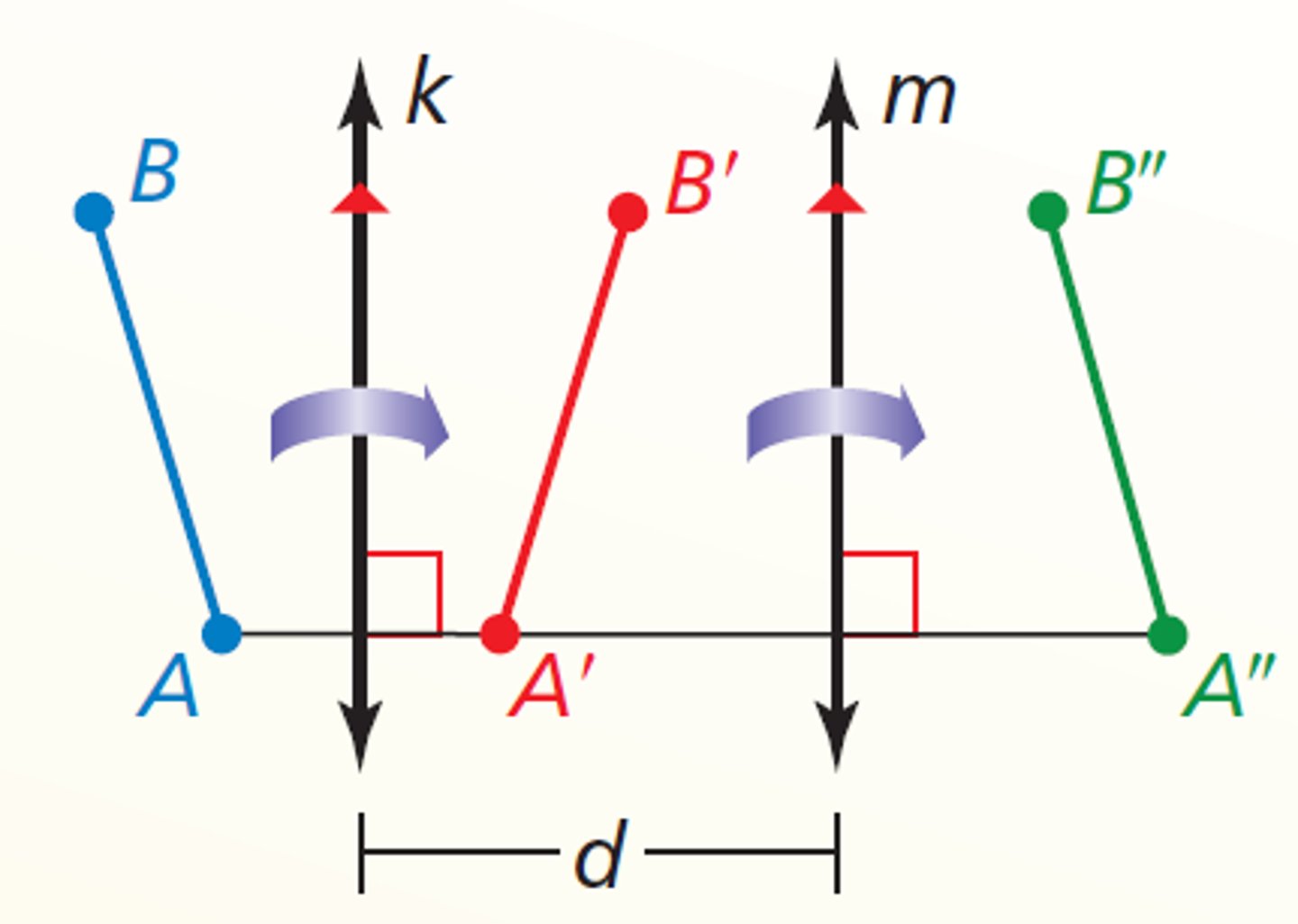
What is the reflection in parallel lines theorem?

If lines k and m are parallel, then a reflection in line k followed by a reflection in line m is the same as a translation

If image A" is the image of A, then

Line AA" is perpendicular to k and m and AA" = 2d, where d is the distance between k and m

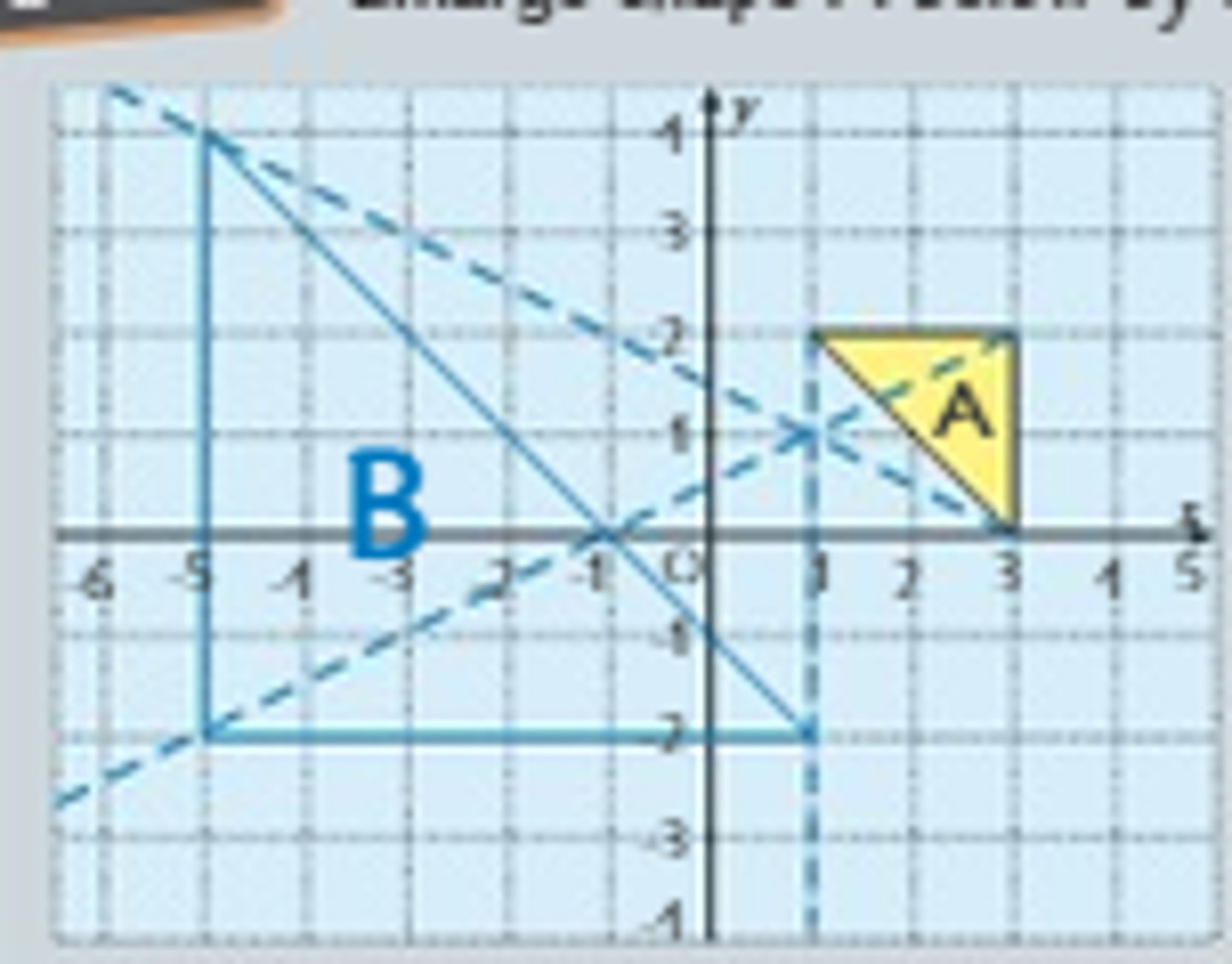
What happens if the scale factor is negative?

The figure rotates by 180 degrees

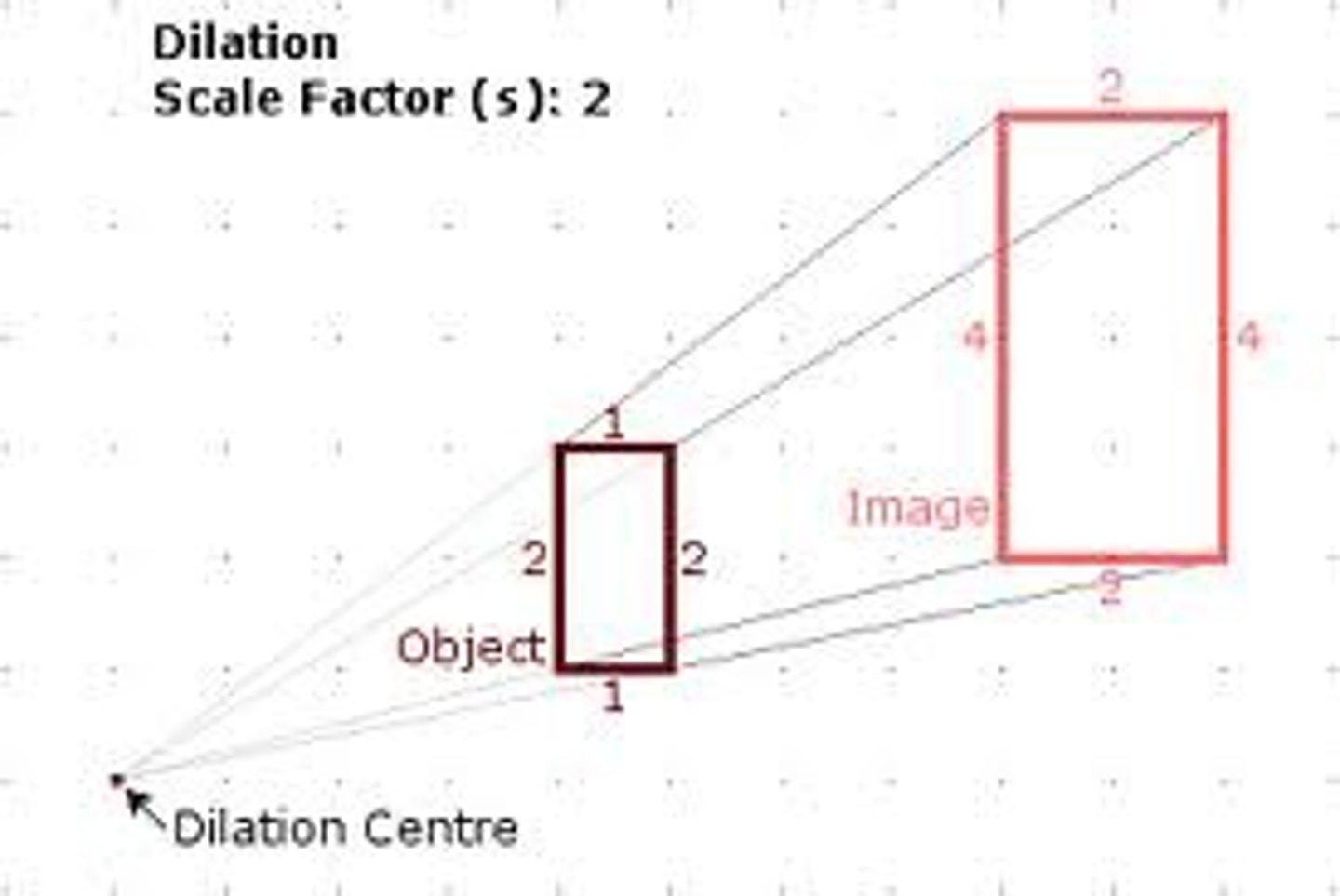
How do you find a scale factor?

Image/pre-image

What is a scalene triangle?

It has no congruent sides

What is an isosceles triangle?

It has at least two congruent sides

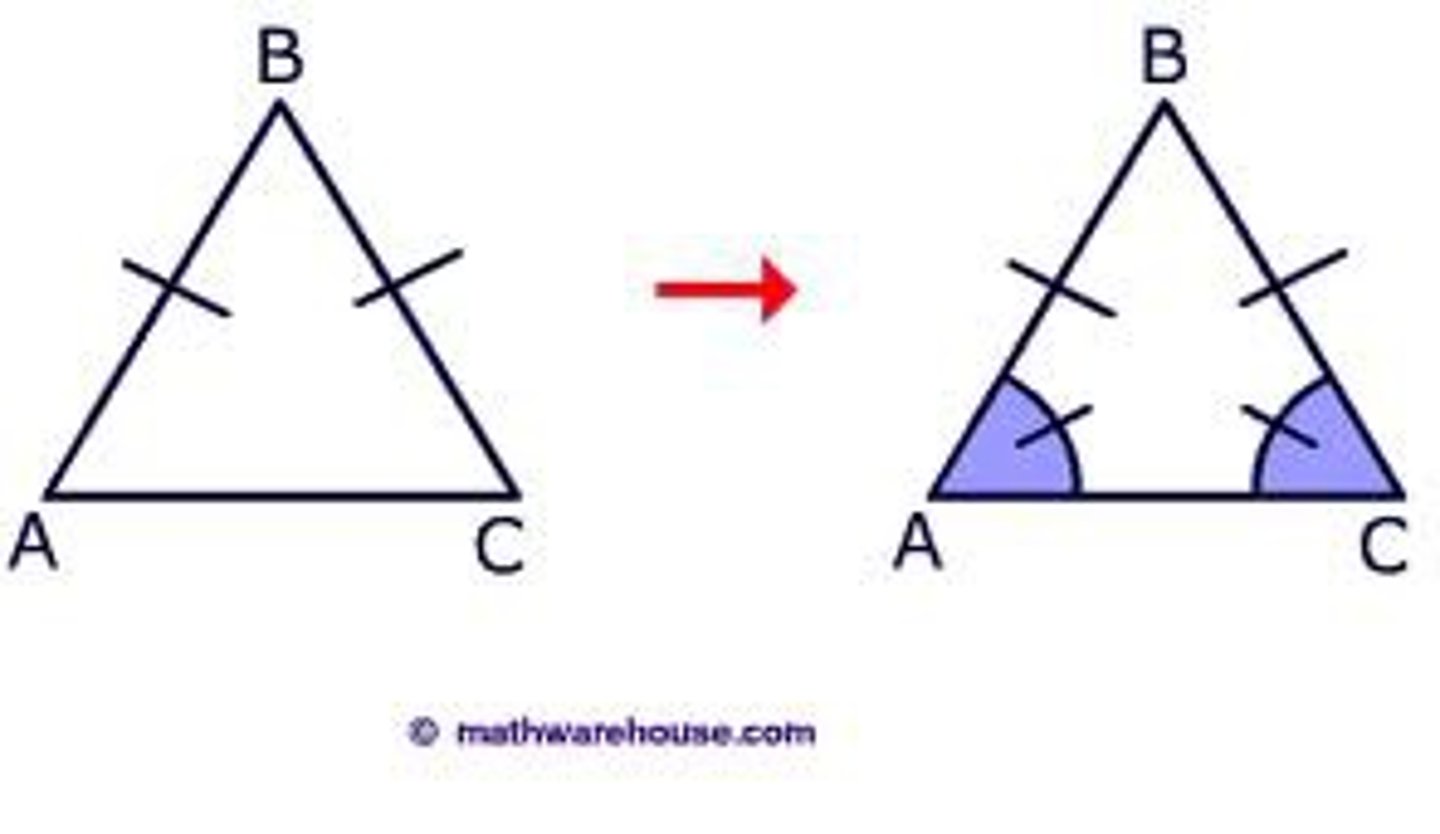
What is an equilateral triangle?

It has three congruent sides

What is an acute triangle?

It has three acute angles

What is a right traingle?

It has one 90 degree angle

What is an obtuse angle?

It has one obtuse anhle

What is an equiangular triangle?

It has three congruent angles

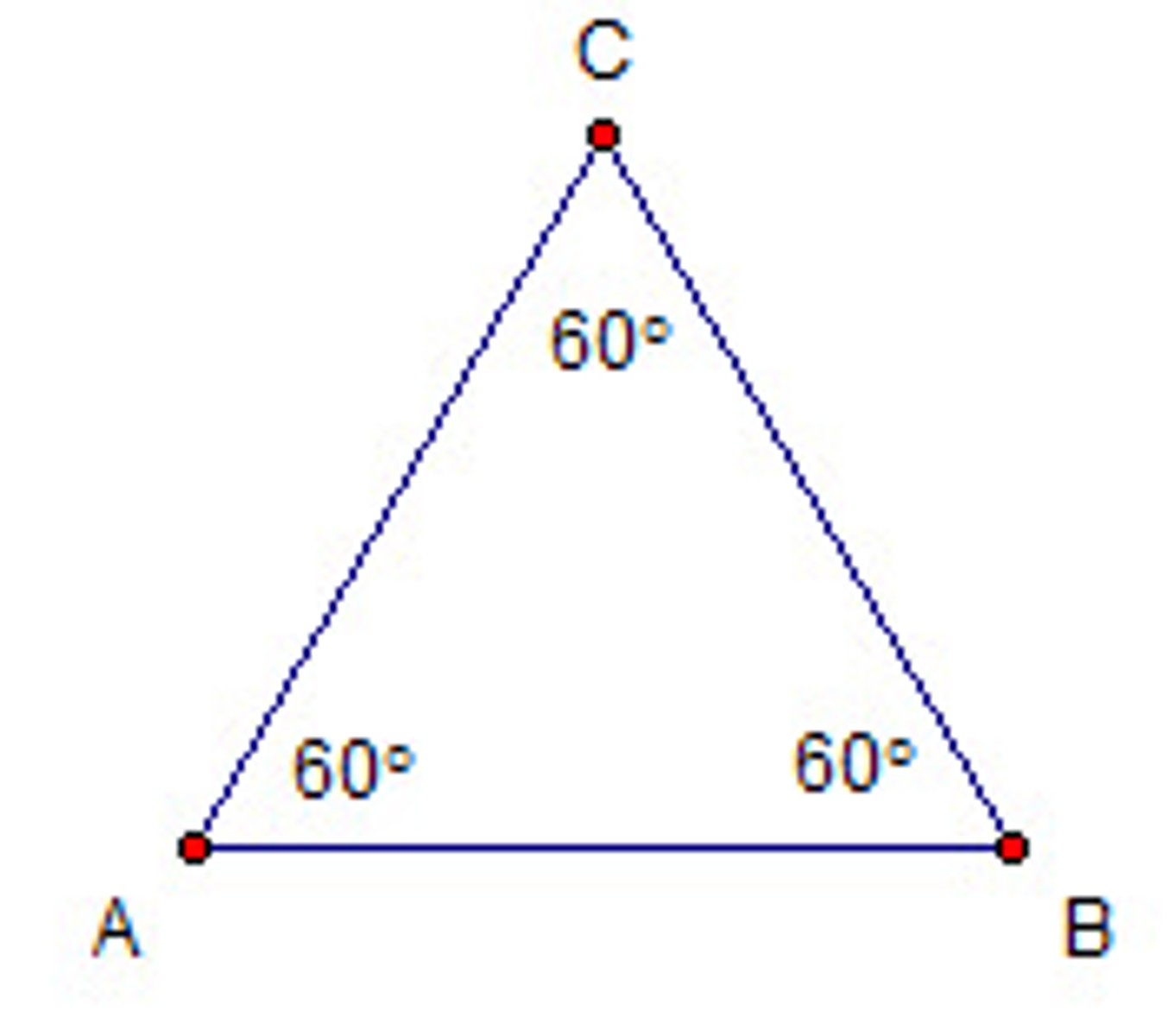
What are the angles of an equiangular triangle?

60 because 180/3 is 60

What do all the angles inside a triangle add up to?

180

What is the triangle sum theorem?

The sum of the measures of the interior angles of a triangle is 180 degrees

What are corresponding parts?

A pair of sides or angles that have the same relative position in two congruent figures

Corresponding angles :

What is the exterior angle theorem?

The measure of an exterior angle of a triangle is equal to the sum of the measures of two nonadjacent interior angles

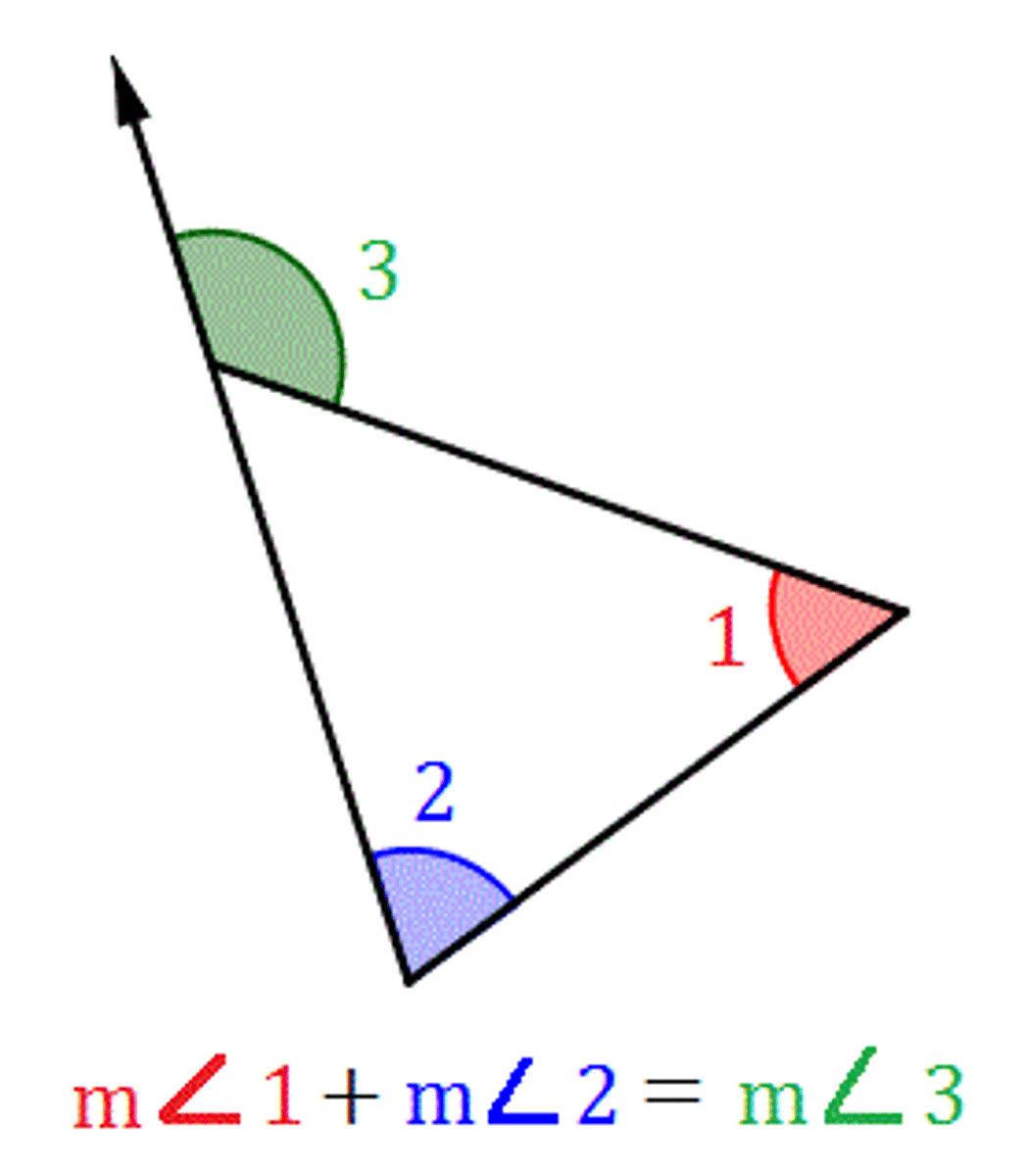
What is the third angles theorem?

If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent

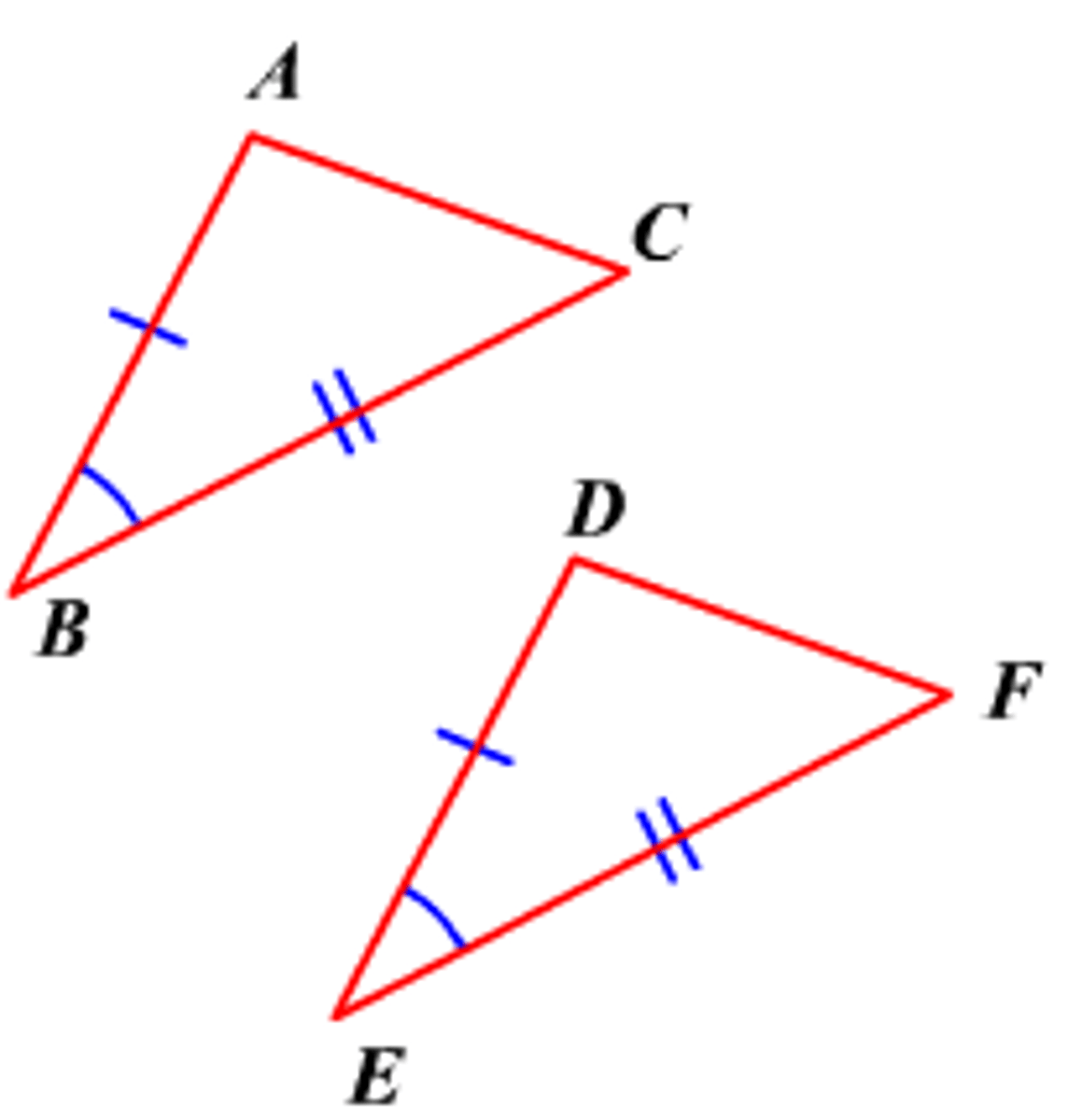
What is SAS?

If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the two triangles are congruent

If segment AB ≅ segment DE,

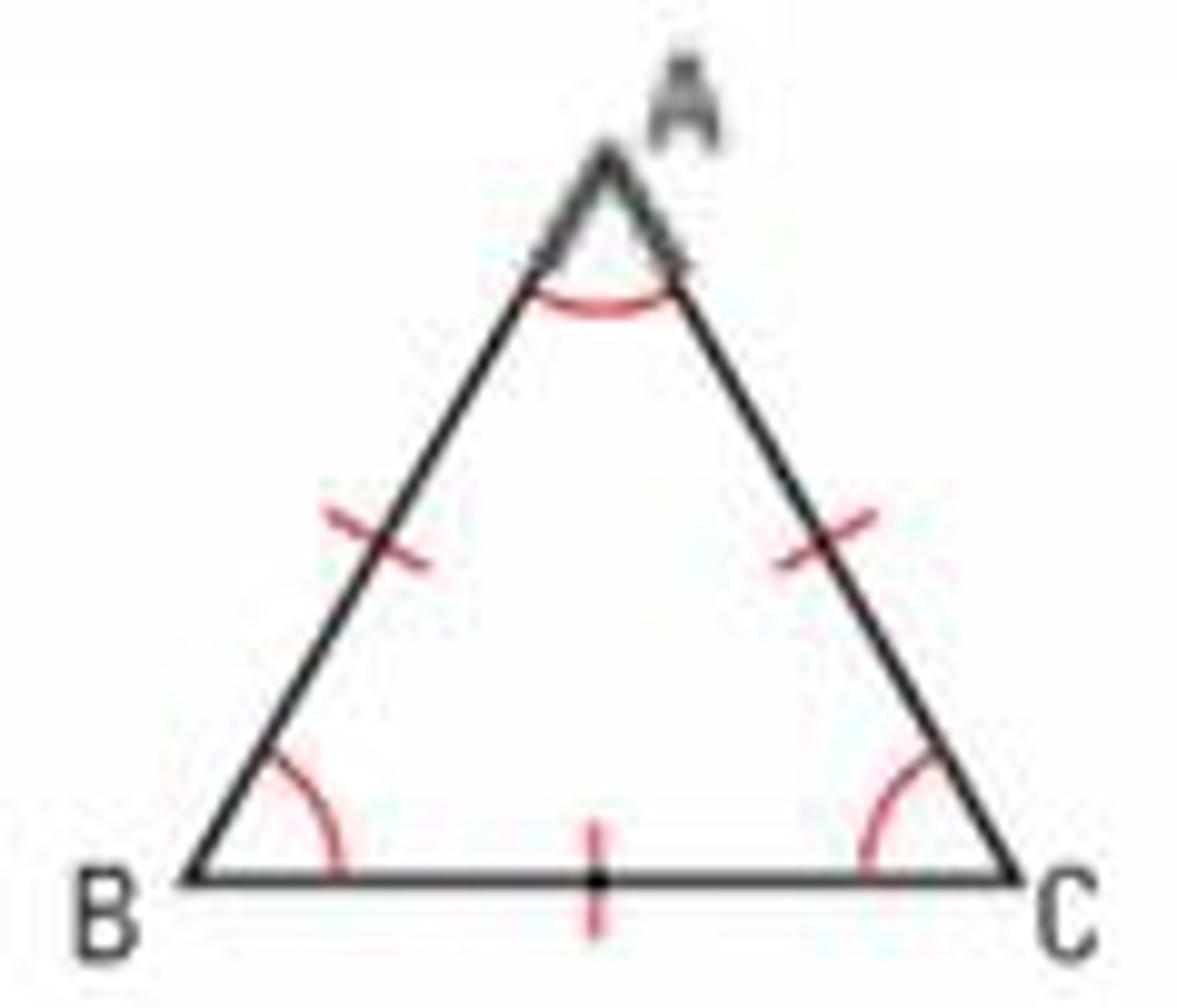
What is base angles theorem?

If two sides of a triangle are congruent, then the angles opposite them are congruent

If seg AB ≅ segment AC, then

What is converse of the base angles theorem?

If two angles of a triangle are congruent, then the sides opposite of them are congruentIf

How much do all the exterior angles of a triangle add up to?

360

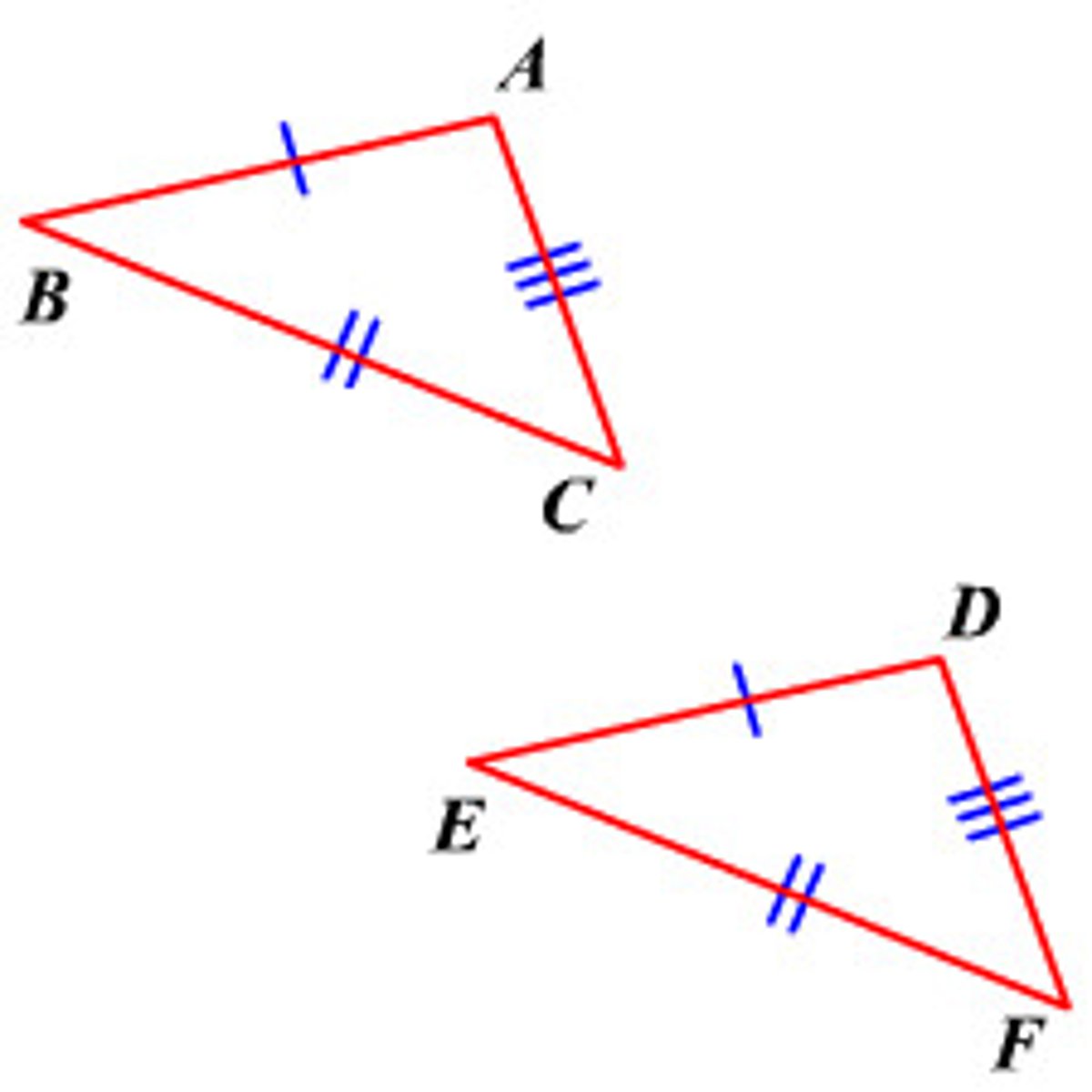
What is SSS?

If three sides of one triangle are congruent to three sides of a second triangles then the two triangles are congruent

What is hypotenuse leg theorem?

If the hypotenuse and a leg of a rt triangle are congruent to the hypotenuses and a leg of a second rt triangle, then the two triangles are congruent

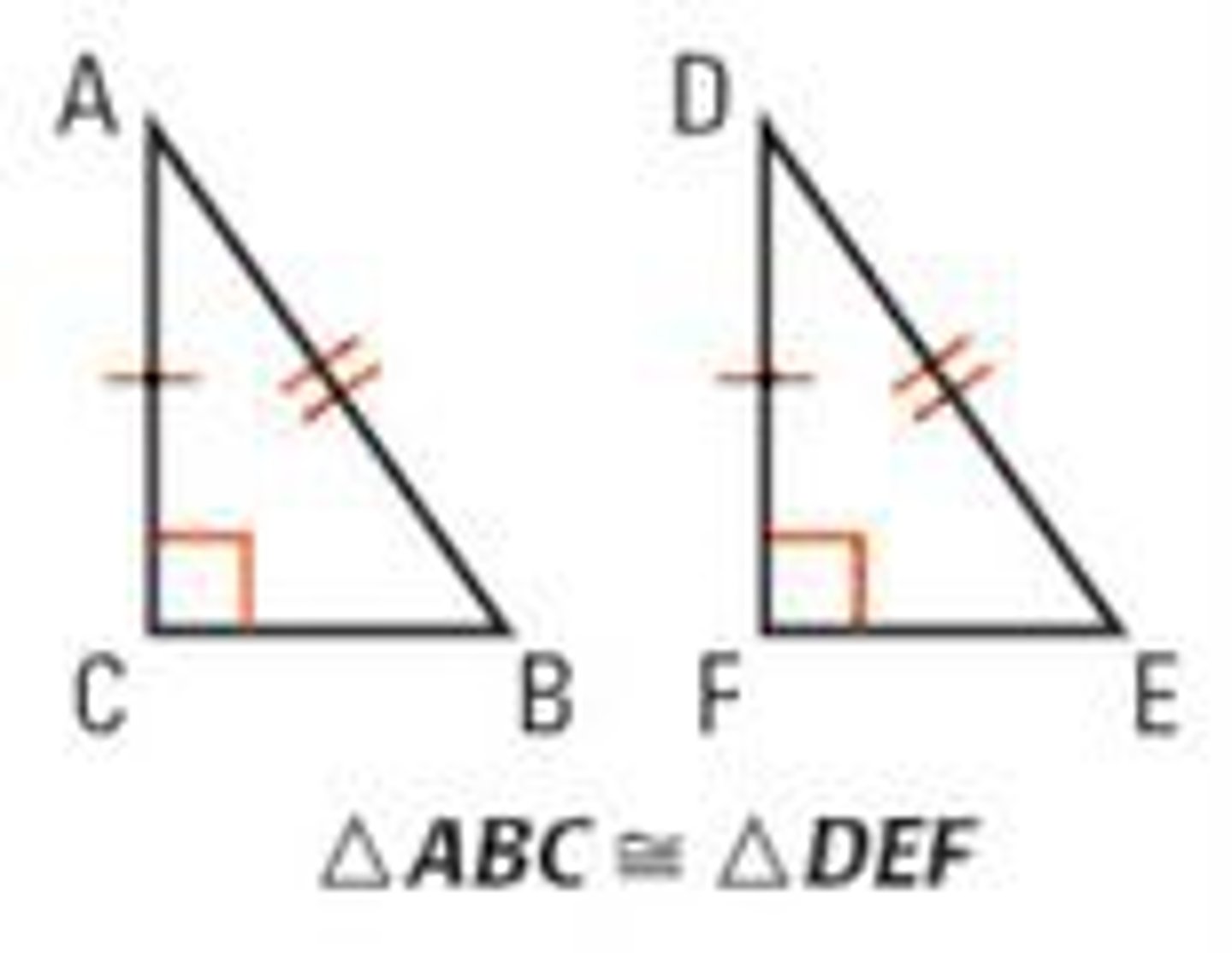
What is ASA?

If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent

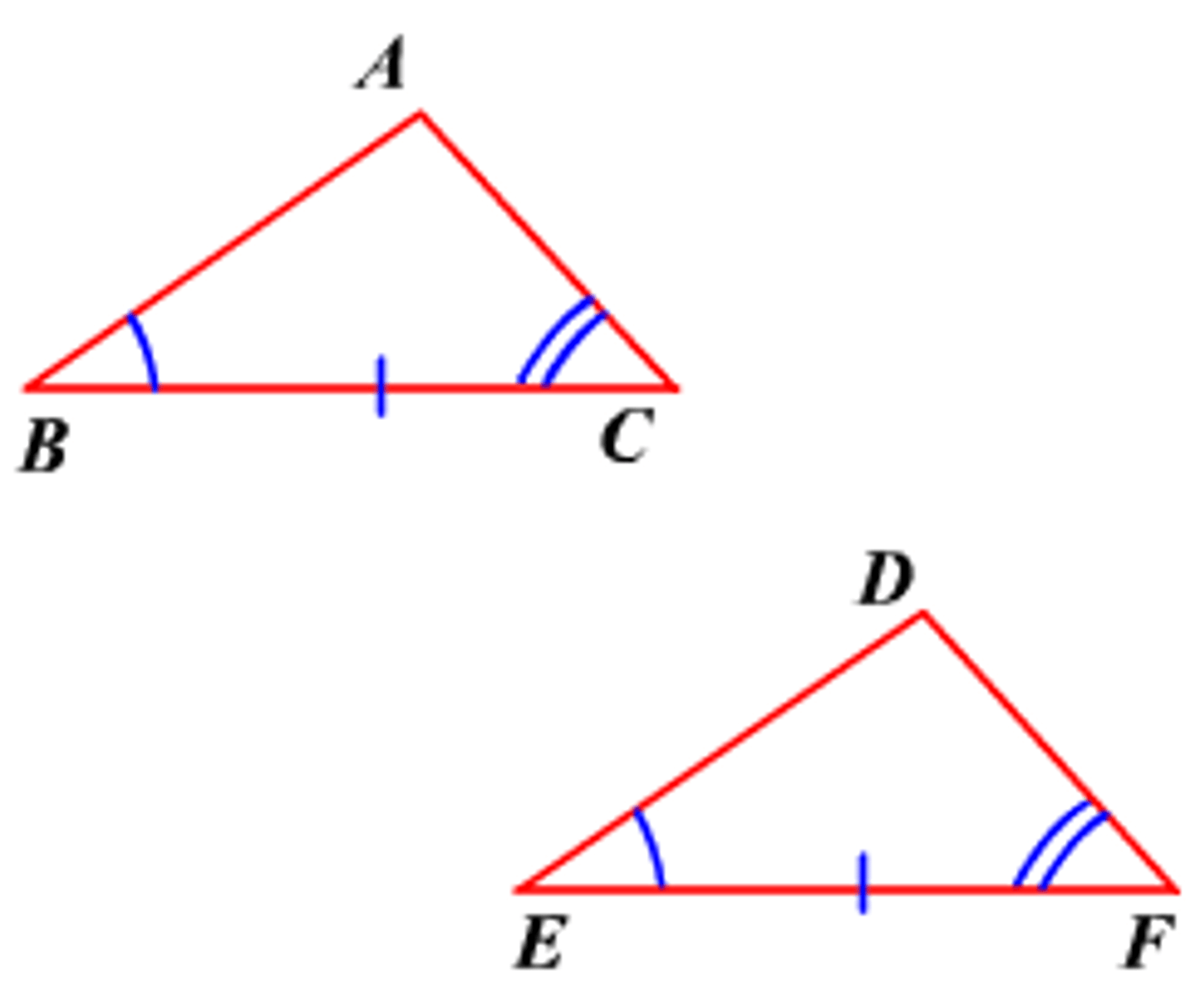
What is AAS?

If two angles and a non-included side of one triangle are congruent to two angles and corresponding non-included side of a second triangle, then the two triangles are congruent

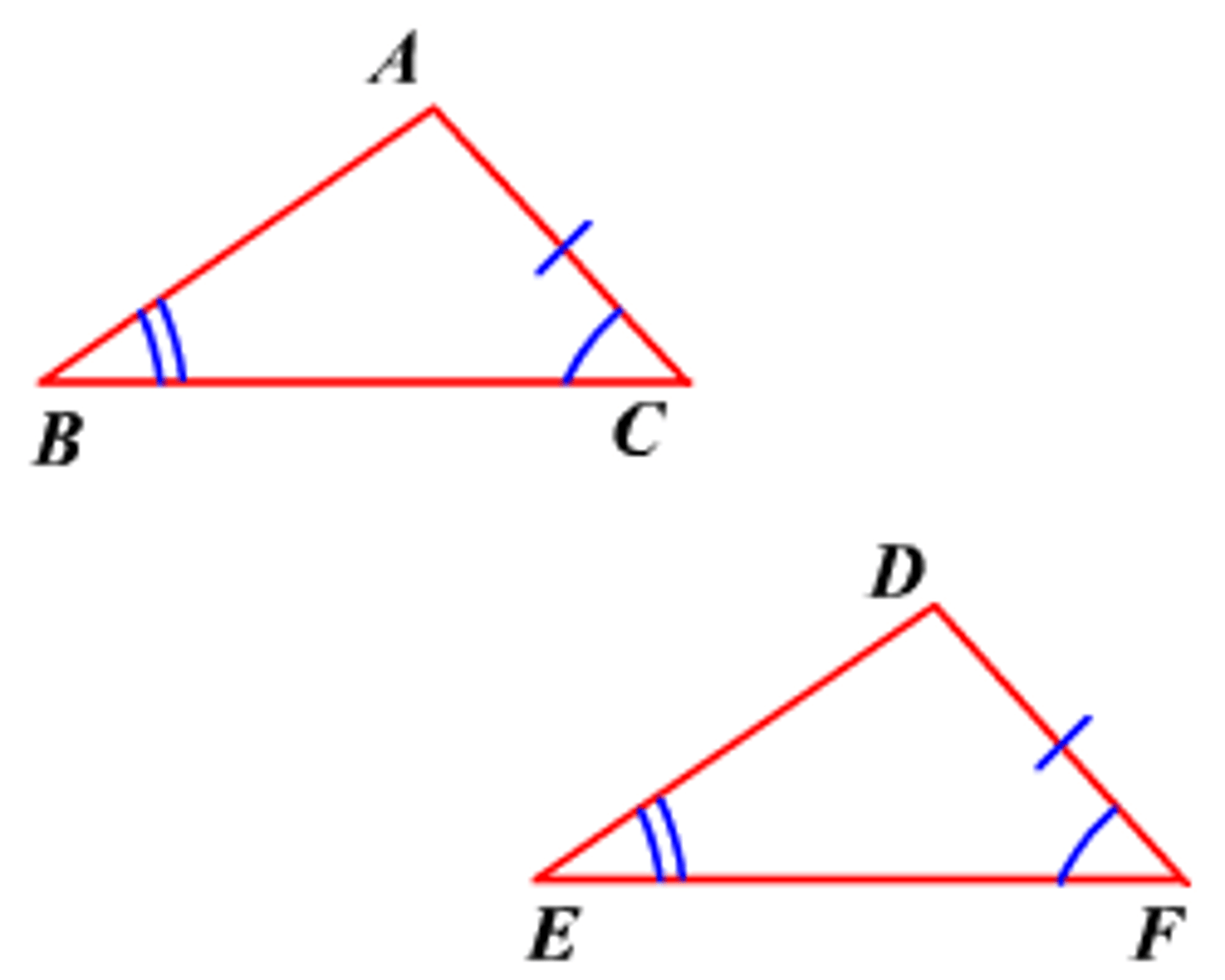
For the proof using definition of congruent triangles, what do you need to prove?

ALL three angles and sides

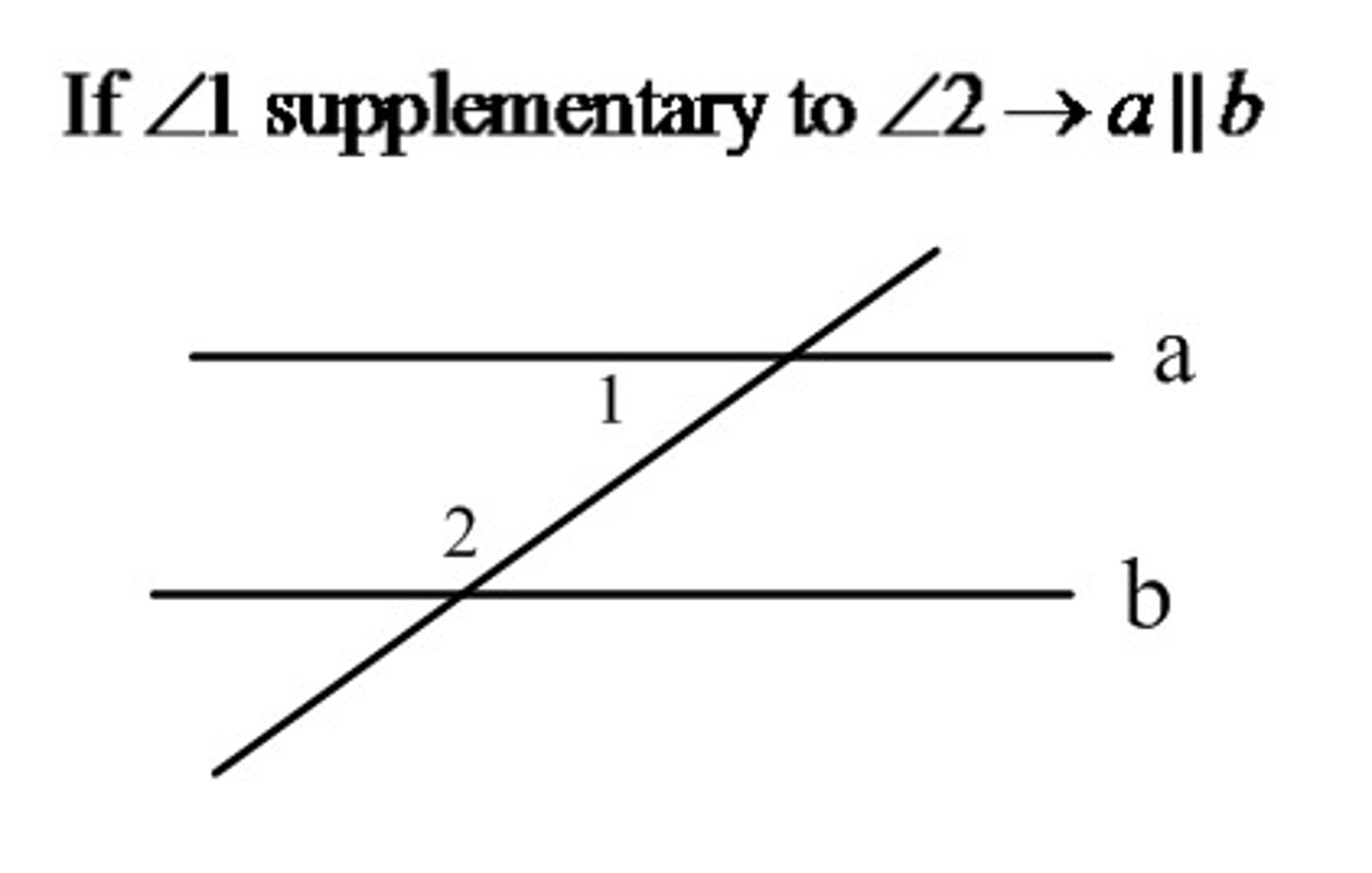
What cannot be used to show that lines m and a are parallel?

Angles one and two are supplementary