Inferential Statistics I-II

What is the purpose of inferential statistics?

To use a sample to make generalizations about a population, determining whether observed effects are likely due to chance or reflect real population effects.

What is the null hypothesis (H₀)?

A conservative baseline assumption stating no relationship between IV and DV; the IV does not affect the DV.
(Always assumed true at the start.)

What is the research/alternative hypothesis (H₁ or H_A)?

The hypothesis the researcher hopes is true; states that there is a relationship or effect of the IV on the DV.

What makes H₀ and H₁ “mutually exclusive and exhaustive”?

• Mutually exclusive: Both cannot be true at the same time.

• Exhaustive: They cover all logical possibilities—there is an effect or there is not.

What is the p-value?

The probability of obtaining the observed data (or more extreme data) if the null hypothesis is true.

What does a low vs high p-value mean?

• High p-value (> 0.05) → Results likely due to chance → retain H₀

• Low p-value (≤ 0.05) → Results unlikely due to chance → reject H₀ (significant effect)

What is alpha (α)?

The threshold for statistical significance; typically 0.05.
If α = 0.05, we accept a 5% chance of committing a Type I error.

What is a Type I error?

Rejecting H₀ when H₀ is actually true (false alarm).
Example: Saying there is an effect when there is none.

What is a Type II error?

Retaining H₀ when H₀ is actually false (miss).
Example: Failing to detect a real effect.

How are Type I errors related to alpha (α)?

Alpha sets the probability of a Type I error.
If α = 0.05 → expect 5 false rejections per 100 experiments (assuming H₀ is true).

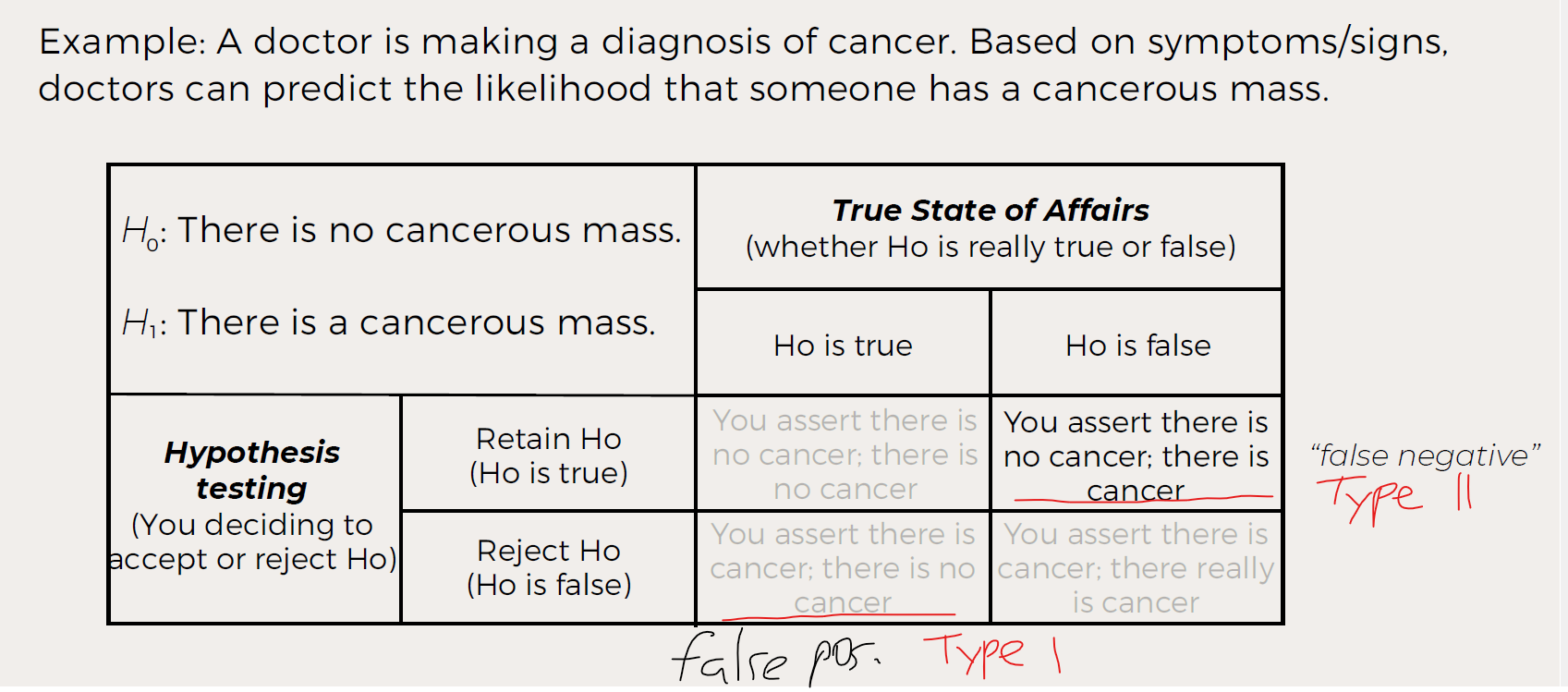
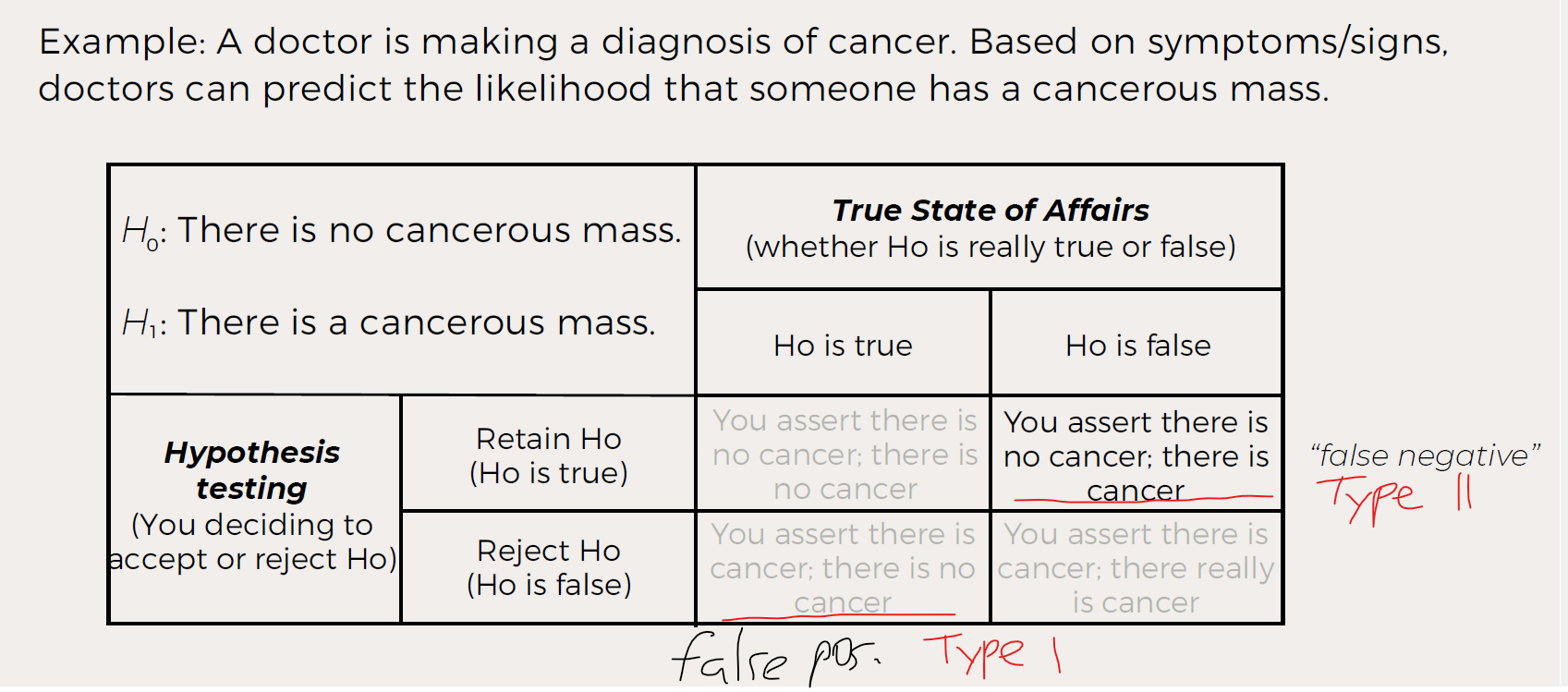
What is the doctor/cancer example illustrating?

• Type I error: Saying “cancer” when there is none (false positive).

• Type II error: Saying “no cancer” when it exists (false negative).

What is statistical power?

The probability of correctly rejecting H₀ when H₀ is false (detecting a true effect).
Power = 1 – β.

What does low power mean?

A higher chance of Type II errors (missing real effects).

What 3 factors influence statistical power?

• Sample size (larger → more power)

• Effect size (larger effects are easier to detect)

• Alpha level (α) (larger α → higher power)

How does increasing sample size affect power?

A larger sample yields more precise estimates → more power, especially helpful when effect sizes are small.

How does effect size influence power?

Larger population differences are easier to detect → higher power.

How does alpha (α) influence power and errors?

• Higher α (e.g., 0.25) → easier to reject H₀ → higher power but more Type I errors

• Lower α (e.g., 0.05) → harder to reject H₀ → lower power but fewer Type I errors

What happens when α = 0.05 in the camera example?

• Very strict; only detects strong movement

• Low Type I error (few false alarms)

• High Type II error (misses burglars)

• Low power

What happens when α = 0.25 in the camera example?

• Very sensitive; detects lots of movement

• High Type I error (false alarms from bugs/shadows)

• Low Type II error

• Higher power (better at catching burglars)

What are the 4 steps of NHST?

• State hypotheses and assume H₀ is true

• Collect data

• Calculate p-value given H₀

• Decide to retain or reject H₀

What does it mean to “reject the null hypothesis”?

The data were unlikely under H₀ (p ≤ 0.05), suggesting a significant IV → DV effect.

What does it mean to “retain the null hypothesis”?

The data were common under H₀ (p > 0.05), so insufficient evidence to say there is an effect.
(Not proving H₀ true—just not enough evidence to reject it.)

B) is correct → what if people get worse after going to office hours? etc. (Possible other outcomes we don’t contest for)

• Yes mutually exclusive (contradict each other)

• Better exhaustive hypothesis: There will be A DIFFERENCE/CHANGE vs directly saying they will do better (change research hypothesis)

  • “People who attend at least 1 office hours session will have a difference in their 217 Final Exam grade compared to students who have never attended an office hours session”.

• A) is correct because p-value > 0.05

  • Could be completely due to chance

B) is correct

A) is correct

What would a Type II error mean in this scenario? Express this in everyday language.

• Accepting the null hypothesis but it’s actually false

• Say Canucks record is the same but it actually changes due to coaching staff

• New coaching staff made a difference when we say they didn’t

B) is correct

C) is correct