Stat unit 1

not that bad

Categorical Variable

Names, labels

ex: marital status, eye color, race

Quantitative Variable

Makes sense to average

ex: height, test scores

Frequency

How many times something occurred

Marginal Distribution

Subset out of the whole sample.

Conditional Distribution

Parts out of a group/subgroup

Individuals

Subjects described by data set

Variable

Characteristic of individual

Association

One variable influences the other. The two are associated, but do not use correlated instead of associated.

Stacked/Segmented Bar Graph

Displays all components of a whole on top of each other as part of a whole bar.

Mosaic Plot

Segmented bar graph but widens the bars to be proportional to their respective sample sizes.

Dot Plot

Each data value is shown as a dot above its respective value on a number line.

Stem and Leaf Plot

Vertical Bar Graph but denotes the points as numbers with EVENLY SIZED BUCKETS. 

Requires a key for the buckets, can just say “5-9” for one bucket

Bar Graph

Denotes the amount of people who answered each response by a vertical y axis.

Histogram

Divides points by frequency and graphs similar to a bar graph, but with conjoined bars and buckets.

MUST INCLUDE A KEY FOR THE BUCKET SIZES. Can be 5 - 9

SOCCS

Shape, Outliers, Center, Context, Spread

Shape

Noteworthy features of graph. Unimodal(one hump), Bimodal(two humps), multimodal(many humps), Skew, or irregular(doesn’t fit any description).

Skew

Distribution of individuals on one side or the other of a graph. Usually the lower, more severe portion of the graph determines the skew.

ex: if the graph is a histogram with most people answering 50-60, but a fair few answered 60-70 and 70-80, we would say the graph is skewed right.

Outliers

Points that are statistical anomalies, that are greater than Q3 + 1.5(IQR) or less than Q1 - 1.5(IQR). 

Center

Can be median or mean depending on the skew of the graph, but describes the center.

Context

Context behind the data. Say “The (variable) typically varies from the mean by about…(s_x with units)“ or “on average, a (variable) is about (s_x with units) away from mean.“

Spread

Describes the distribution of the graph. Can use range, standard deviation, or IQR.

Range

Max - Min

IQR

Q3 - Q1

Standard Deviation

Formula given on equation sheet but essentially the average difference between an individual and the mean.

denoted by s_x on equation sheets and in writing

Median

The middle term of a distribution.

ex: in a sample of 11 people, the 6th person’s (after ordering from least to greatest) response would be the median. If the group was reduced to 10, the median would be the average of the 5th and 6th people’s answers.

Q3

The median of the upper half of the graph, excluding the median if it is just the middle term. If the median is the average of the two closest terms, take the greater term and include it in the median calculation.

Q1

The median of the bottom half of the graph, excluding the median if it is just the middle term. If the median is the average of the two closest terms, take the lower term and include it in the median calculation.

IQR

Q3 - Q1

Mean

Average of all responses from the sample. denoted by x with a bar on top in the equation sheet.

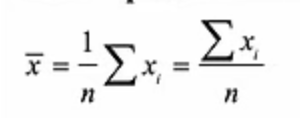
5 number summary

Min, Q1, Median, Q3, Max

Box Graph

Uses the 5 number summary to graph the distribution. Uses the Q1, median, and Q3 values to draw the box in the middle, with the median denoting the line in the middle of the graph. Min and Max describe the outer “stops“ of the graph.

Outliers in Box Graphs

Outliers are denoted either by an asterisk if wished, with the max/min being reduced to the next greatest/lowest point. If not denoted, nothing is needed.

Getting 1 Var Stats on graphing calculator

STAT —> CALC —> 1-Var Stats

How to create a list on graphing calculators

STAT —> EDIT —> input values into a list, likely L1

How to graph various graphs with graphing calculator

STAT —> WINDOW(set appropriate range) —> STAT PLOT(turn appropriate list on) —> GRAPH