6 Properties of Limits, Techniques and Computation (Theory)

3 Basic Properties of Limits

(1) limit of a constant

(2) limit of a variable

(3) right-sided and left-sided limits of rational functions

Basic Limit Property: Limit of a Constant

Basic Limit Property: Limit of a Variable

Basic Limit Property: One-Sided Limits of Rational Functions

What does this assumption mean?

(1) essentially if just two limits approach the same point

You can perform operations on limits if…

(1) if the limit of two different functions approach the same point you can apply the properties of the limits: meaning you can add, subtract, multiply, divide, separate exponents, and separate roots

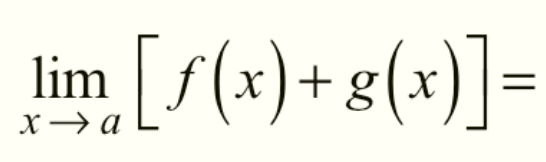
Addition of Limits

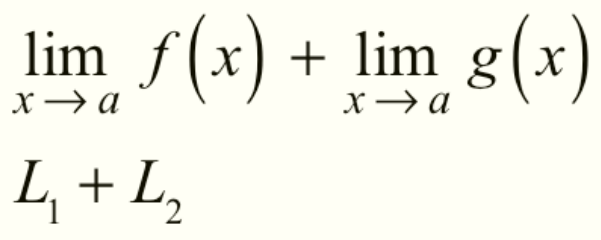
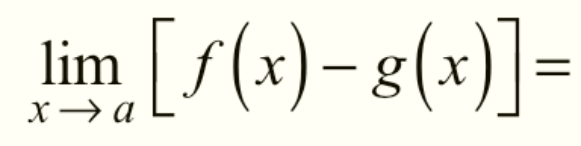
Subtraction of Limits

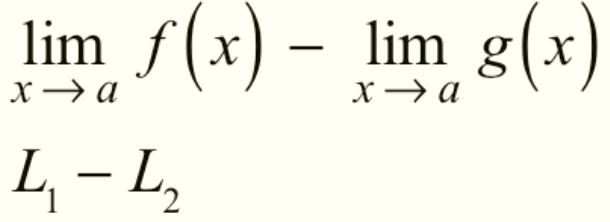
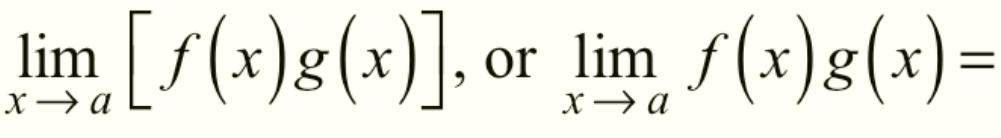
Multiplication of Limits

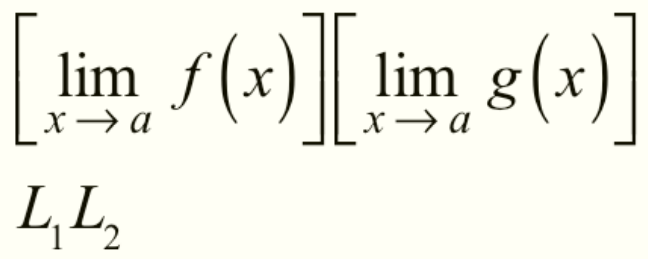
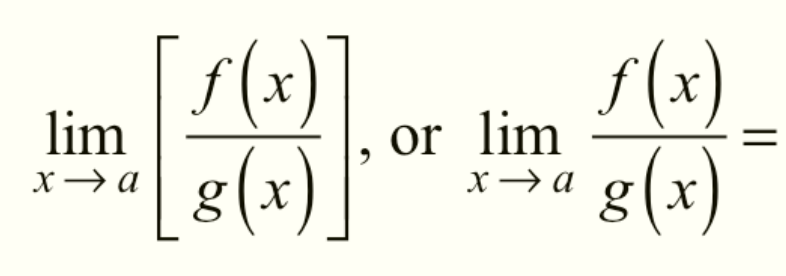
Division of Limits

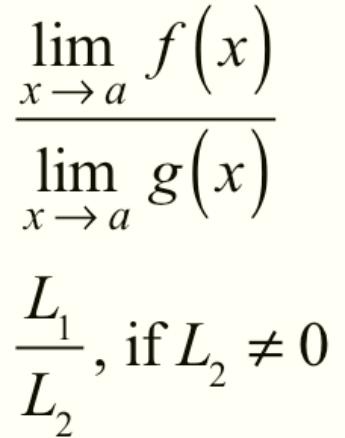
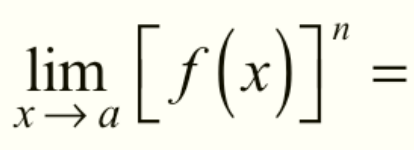
Power (Exponent) Property of Limits

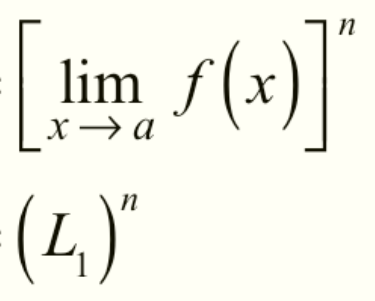
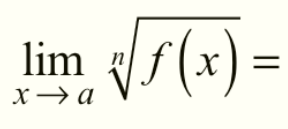
Root Property of Limits

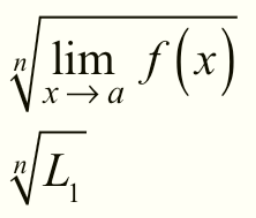
Steps to Finding the Limits of Polynomials (In General)

(1) To find the limit of a polynomial, just plug in “a,” and solve, just plug in the number and evaluate

Steps to Finding the Limits of Rational Functions (In General)

(!) To find the limit of rational functions, just plug in “a,” and solve, just plug in the number and evaluate

Steps to Finding the Limits of Radical Functions (In General)

(1) To find the limit of radical functions, just plug in “a,” and solve, just plug in the number and evaluate

Steps to Finding the Limits of Rational Functions (Holes, Factoring)

Step 1: Factor the denominator and solve for x’s to check if the point “a,” is one of the solutions of will make your denominator equal zero

Step 2a: If the denominator equals zero, factor out both numerator and denominator to see if any factors cancel,

— if they can cancel, you have a hole: plug in point “a” and evaluate as usual to find the limit

— if they do not simplify (cancel out), you have an asymptote

Steps to Finding the Limits of Rational Functions (Asymptotes, Factoring)

Step 1: Factor denominator and check for domain problem

Step 2: Factor denominator and numerator and simplify

— if they do not simplify (cancel out), you have an asymptote

Step 3: Sign Analysis Test
- set both your numerator and denominator equal to zero respectively, solve for points, and then plot them into your graph
- pick points around those points so you can figure out the behavior of your asymptote to find the limit

Step 4: Find the Limit
- if asymptotes both go to the same direction — the limit exists
- if asymptotes go to different directions — the limit doesn’t exist

Steps to Finding the Limits of Rational and Radical Functions (Rationalization)

Step 1: Check for domain problems in the denominator, plug in point “a” to see if denominator equals zero

Step 2: Rationalize the denominator or the numerator by (1) multiplying the rational by itself or (2) multiplying by the conjugate

Step 3: Simplify the denominator or numerator to get rid of the radical

Step 4: Leave either the numerator or the denominator unfactored

Step 5: Cancel out factors and simplify

Step 6: Find the limit

— plug in point “a” and evaluate as usual to find the limit

— Sign Analysis Test

Sign Analysis Test

Step 1: Set both your numerator and denominator equal to zero respectively, solve for points

Step 2: Plot those points into your graph

Step 3: Pick points around those points so you can figure out the behavior of your asymptote to find the limit

Limits are your __(1)__ on the _(1)_-axis

(1) outputs

(2) y