Lecture 4: Models

model

-simplified or idealised representation of a more complex thing

statistical models

-description of mathematical relationship between variables, that hold under specific assumptions

-doesn’t attempt to explain anything → just describing relationship

theoretical models

-description of the relationship between different mental processes

-makes assumptions about the nature of these processes

-attempts to explain and provide further predictions

behaviourism 

-suggested mind is like a black box → don’t know what is happening inside and we shouldn’t investigate it 

-only care about how input changes output behaviour 

cognitive psychology

-mind is like a black box

-if change inputs in a certain way and record outputs in a certain way can maybe make conclusions about processes inside black box

-enough experiments can understand what is happening in black box

box-and-arrow models

-models that describe the relationship between different mental processes, under the assumption that the mind operates like multi-staged information-processing machine

-not saying this is how cognitive processes works → just a simplified version that captures key elements the researcher wants to emphasise

-can add more boxes and arrows developing on previous models

cognitive models

-manipulating the input and observing the output can provide a glimpse to the machination of the mind and allow us to test our models 

-can expand and change models based on results 

formal cognitive models

-a mathematical description of the relationship between two variables

-usually expressed through computer code

-black box seen as working in same way as computers

simplification

-making something simpler

-don’t need to capture every small detail of a cognitive process

-only capturing parts we deem critical of what we are trying to represent

abstraction

-generating general rules and concepts from specific information 

-depends on question you are asking and what you are trying to convey 

-making the model useful for goals 

prediction and/or explanation

-models in science must produce some predictions

-predictions can be directional or numerical

-non-scientific theories explain after the fact but cannot provide falsifiable predictions

directional predictions

-give direction of what you think will happen

-no quantifiable amount specified - just direction

numerical predictions

-giving specific value with specific prediction

-can be more or less accurate

using models to predict and explain

1. data

2. hypothesis

3. model

4. theory

5. framework

data (using models to predict and explain)

-collected observations, often as part of an experiment

hypothesis (using models to predict and explain)

-narrow testable statement

model (using models to predict and explain)

-schematic representation of a theory

-more limited in scope

theory (using models to predict and explain)

-scientific proposition that provides relations between phenomena

framework (using models to predict and explain)

-conceptual system that defines terms and provides context 

explanation without prediction

-models of schizophrenia can indicate causes but cannot predict individual cases

-model predicts group differences but not individual cases

-consistent with theoretical models

prediction without explanation

• prediction error model

-some models can predict whether an individual will develop AD, even though we don’t understand the factors that explain AD

-may predict average directional differences between conditions

-prediction ignorant to components - do not know what variables mean and just observe correlation → consistent with statistical models

informal cognitive models

-verbal description of the relationship between different cognitive procedure

• assumptions are implicit

• provides directional predictions

formal/computational models

-mathematical description of the relationship between different cognitive procedure, often instantiated via computer program/simulation

• assumptions are explicit

• provides numerical predictions

using formal models to explain 

1. data point 

2. hypothesis 

3. implementation → specific instantiation of a specification → computer program able to simulate and predict numerical outputs from input 

4. specification → formal description of the relations described by a theory → formal model comprised of symbolic representations 

5. theory 

6. framework 

more accurate predictions (strengths of formal models)

-having a numerical simulation allows us to see if the model provides unreasonable predictions

-help us select which experiments to perform

-numerical predictions provide a more subtle form of hypothesis testing → can see how close a model is to predicting an actual result

counter-intuitive predictions (strengths of formal models)

-model can clearly describe which predictions follow from a model

-with informal models, it’s hard to notice when they make counter-intuitive predictions → formal models clearly produce such predictions

-numbers do not always match intuition (informal models) and intuition can go awry → formal models can show intuitions don’t match theory in an objective way due to theory being counter-intuitive 

benefits of explicit assumptions (strengths of formal models)

-by making assumptions explicit, can reveal unanswered questions, flaws in our reasoning, contradictory or unreasonable assumptions

-can make assumptions transparent for others to see 

limits of formal models

-require substantial expertise 

-only transparent for experts who can understand them 

-only comparable against other computational models 

-sometimes numerical predictions are premature 

-changing the model is costly time-wise and can limit progress 

-making a model simulate a cognitive task does not necessarily teach us much about cognition 

hype timeline

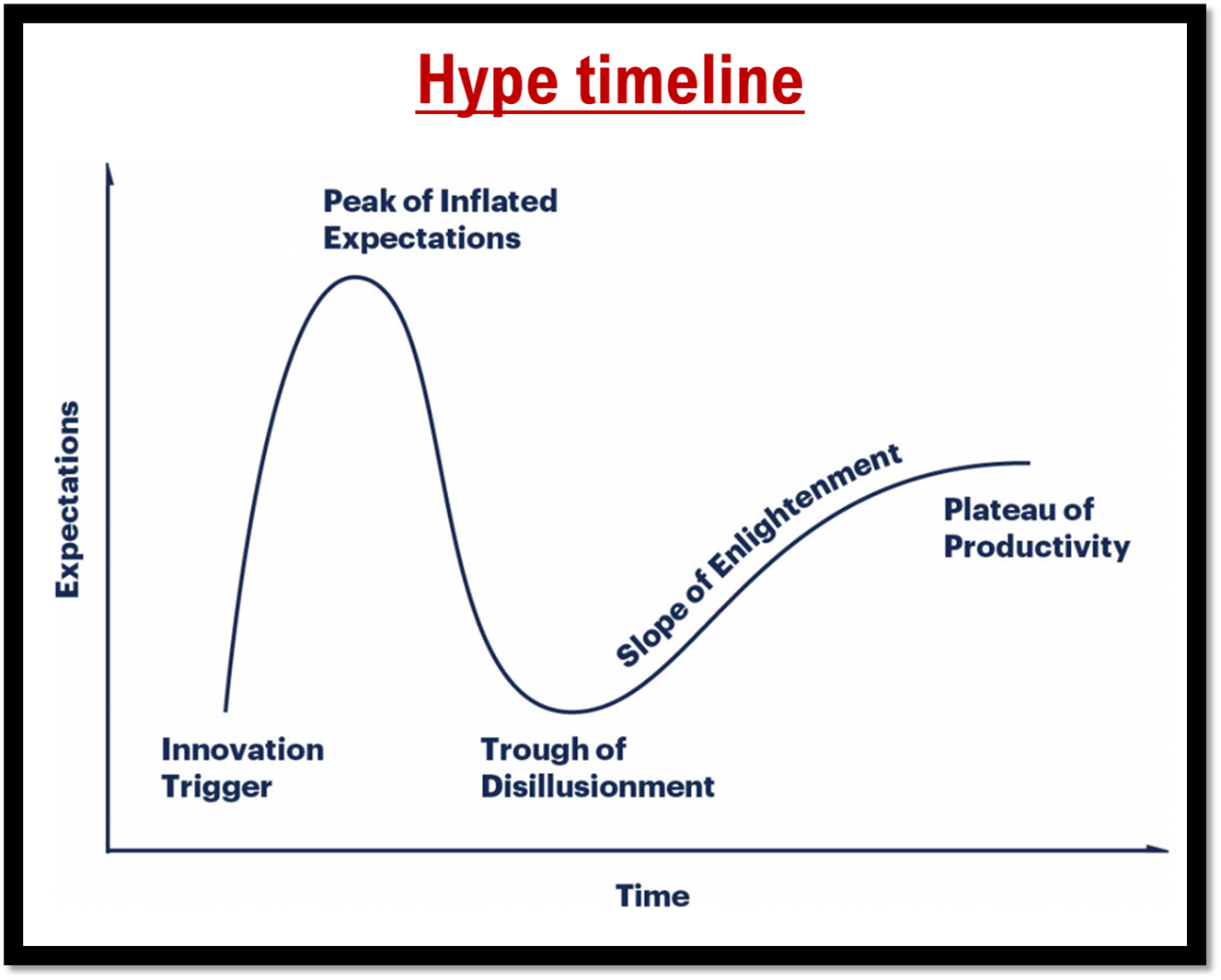
-lot of hype surrounding new tools

-but once they are understood better they reach a plateau of productivity

David Marr

-suggested we can understand and model a system at a number of levels

-pointed to three levels of understanding:

1. computation → problem being solved

2. algorithm → steps/rules to solve it

3. implementation → actual machinery

-suggested that something is more easily understood from its function rather than a single data point or the mechanisms (hardware) in which a function is embodied (top-down approach)

bottom-up approach (neuroscience & Marr)

1. implementation → machinery of neural circuits

2. rules → what representations and algorithms can we generate, given specific neural circuits?

3. problem → what problems are solved by these algorithms?

top-down approach (neuroscience & Marr)

1. problem → what is the problem we’re trying to solve 

2. rules → what representations and algorithms can solve this problem? 

3. implementation → how can these representations and algorithms be implemented in neural circuits? 

-much easier to disqualify bad explanations

-but not practical so bottom-up approach is more common

theory and implementation

-researchers can: 

• focus on implementation without theory 

• focus on theory without implementation

• approach problem assuming all levels (problem, rules and implementation) inform one another