Unit 2 Exploring Bivariate Data Vocabulary

Response Variable

Measures an outcome of a study

Explanatory variable

May help predict or explain changes in a response variable

Two-way table

A table of counts or relative frequencies that summarizes data on the relationship between two categorical variables for some group of individuals

Marginal relative frequency

Gives the percentage or proportion of individuals in a two-way table that have a specific value for one categorical variable. A [blank] relative frequency is calculated by dividing a row or column total by the total for the entire two-way table

Joint relative frequency

Gives the percentage or proportion of individuals in a two-way table that have a specific value for one categorical variable and a specific value for another categorical variable. A [blank] relative frequency is calculated by dividing the value in one cell by the total for the entire two-way table

Conditional relative frequency

Gives the percentage or proportion of individuals that have a specific value for one categorical variable among a group of individuals that share the same value of another categorical variable (the condition). A [blank] relative frequency is calculated by dividing the value in one cell of a two-way table by the total for the appropriate row or column

Segmented bar graph

Displays the distribution of a categorical variable as segments of a bar, with the area of each segment proportional to the number of individuals in the corresponding category

Mosaic plot

A modified segmented bar graph in which the width of each bar is proportional to the number of individuals in the corresponding category

Association

A [blank] between two variables if knowing the value of one variable helps us predict the value of the other. If knowing the value of one variable does not help us predict the value of the other, there is no [blank] between the variables

Scatterplot

Shows the relationship between two quantitative variables measured for the same individuals. The values of one variable appear on the horizontal axis, and the values of the other variable appear on the vertical axis. Each individual in the data set appears as a point in the graph

Positive association

Two variables have a [blank] association when the values of one variable tend to increase as the values of the other variable increase

Negative association

Two variables have a [blank] association when the values of one variable tend to decrease as the values of the other variable increase

No association

There is [blank] association between two variables if knowing the value of one variable does not help us predict the value of the other variable

Correlation

Gives the direction and measures the strength of the linear association between two quantitative variables

r

Correlation symbol

Correlation (formula)

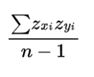
r=

Regression line

A line that models how a response variable y changes as an explanatory variable x changes. [blank] lines are expressed in the form ŷ = a + bx, where ŷ (pronounced “y-hat”) is the predicted value of y for a given value of x

ŷ

y-hat or regression line

Extrapolation

The use of a regression line for a prediction outside the interval of x-values to obtain the line. The further we [blank], the less reliable the predictions become

Residual

The difference between the actual value of y and the value of y predicted by the regression line. That is, [blank] = actual y – predicted y (or ŷ)

y-intercept

Predicted value of y when x = 0

Slope

The among by which the predicted value of y changes when x

b

The slope

a

The y-intercept

Least-squares regression line

The line that makes the sum of the squared residuals as small as possible

Slope (formula)

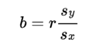
y-intercept (formula)

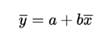
Residual plot

A scatterplot that displays the residuals on the vertical axis and the values of the explanatory variable (or the predicted values) on the horizontal axis

Coefficient of determination

Measures the percent reduction in the sum of squared residuals when using the least-squares regression line to make predictions, rather than the mean value of y. In other words, [blank] measures the proportion (or percentage) of the variation in the response variable that is accounted for (or explained) by the explanatory variable in the linear model

r²

Coefficient of determination

Standard deviation of the residuals

Measures the size of a typical residual. That is, [blank] measures the typical distance between the actual y-values and the predicted y-values

s

Standard deviation of the residuals

High leverage

Points with [blank] in regression have much larger or much smaller x-values than the other points in the data set

Outlier

A point in a regression that does not follow the pattern of the data and the has a large residual

Influential point

Any point in a regression that, if removed, substantially changes the slope, y intercept, correlation, coefficient of determination, or standard deviation of the residuals