ANOVA

ANOVA

• Compare 2 or MORE treatments / groups

• Compares groups to see if they are SIGNIFICANTLY DIFFERENT from each other

• Shows amount of OVERLAP between Group Variance

• Based on VARIANCE instead of Sample Mean Difference 

T-Test (ERROR w/ doing MULTIPLE T-Tests)

- Type I Error ← ANOVA adjusts for this

- Slower ← ANOVA is much quicker

- Shows Significance in Mean Difference ← ANOVA shows Overall Significance in Group Differences

ANOVA FORMULA:

F = Variance (DIFFERENCE) between Sample Means / Variance (DIFFERENCE) EXPECTED w/ NO treatment effect

ANOVA Terminology

FACTOR (IV)

• Main Variable that splits people into different groups in ANOVA

- What category the subjects are put into

EXAMPLE)

1. Temperature Condition (50, 70, 90) → Factor = Temperature

2. Types of Therapy (CBT, Medication, Control) → Factor = Therapy Type

3. Class Year (Freshmen, Sophomore, Junior, Senior) → Factor = Class Year

LEVELS

• Specific groups INSIDE your IV (Factor)

EXAMPLE)

Factor : Temperature

Level : 50, 70, 90

Factor : Class Type

Level : Freshmen, Sophomore, Junior, Senior

Appropriate Research Designs for ANOVA

1. Independent-Measures

2. Repeated-Measures

3. Studies with more than ONE Factor

ANOVA Hypotheses

1. Null Hypotheses

• Treatment has NO effect on Dependent Variable

H_0: μ_1 = μ_2 = μ_3

2. Alternative Hypotheses

• At least ONE Population Mean is Different from Another

H_1: μ_1 ≠ μ_2 ≠ μ_3

H_1: μ_1 = μ_2 ≠ μ_3

ANOVA Logic

Total Variability

• Combine ALL the scores into ONE general measure of Variability 

Between-Treatment Variability

• How DIFFERENT Group Means are from Each Other

- AKA, how much difference exists between the treatment conditions

EXAMPLE)

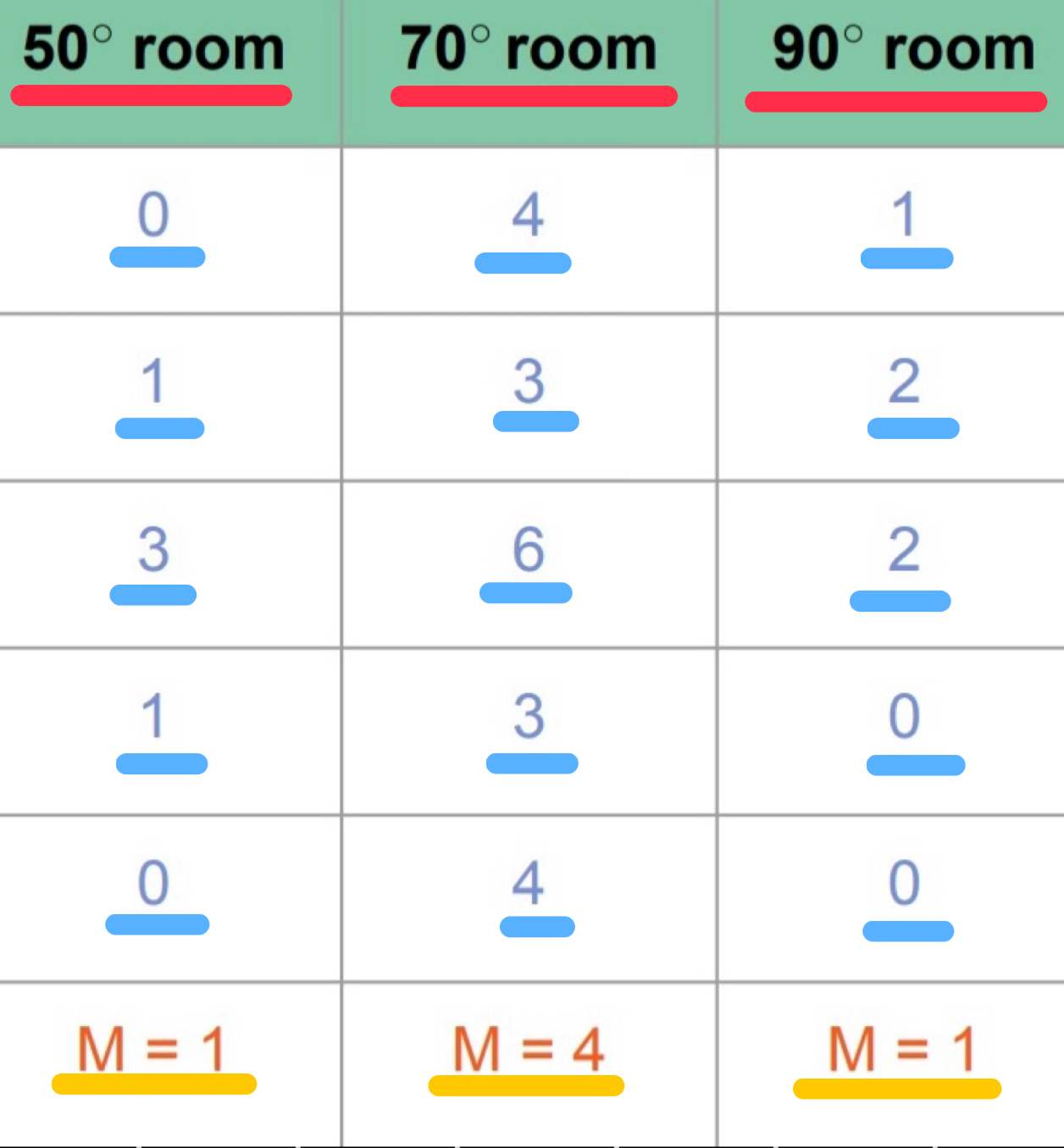
1) 50 Degree room → Mean =1

2) 70 Degree room → Mean = 4

3) 90 Degree room → Mean = 1

70 Degree room has HIGHER Mean → Between-Group Variability BIG

• If Groups MEANS are FAR APART → Treatment(Temp.) actually MATTERS

• If Groups are CLOSER TOGETHER → Treatment(Temp.) DOESN’T MATTER

- AKA, If all Group MEANS the SAME/CLOSER → Between-Group Variability SMALL/NONE

Within-Treatment Variability

• How Much do people Vary INSIDE the SAME GROUP

EXAMPLE)

50 Degree room Scores: 0, 1, 3, 1, 0 … They VARY a LITTLE/SIMILAR (same pattern for other Groups)

• People INSIDE Each Group are SIMILAR → Within-Group Variability SMALL

• If people INSIDE Each Group VARY a LOT → Within-Group Variability BIG

Explanations of Variability

Systematic Treatment Differences

• Differences CAUSED BY Treatment/FACTOR

• Group DIFFERED b/c Treatment/FACTOR Had an EFFECT

Random, Unsystematic Differences

• Differences CAUSED just b/c people Vary Naturally

• Random Noise → NOTHING to do W/ Treatment/FACTOR

- Result of Individual Experiences

- Result of Experimental Error

F-Ratio

GENERAL FORMULA:

F = Variance BETWEEN Treatments / Variance WITHIN Treatments

IT’S ALSO KNOWN AS

F = Systematic Treatment Effects + Random, Unsystematic Differences / Random, Unsystematic Differences

NOTE: Denominator = Error Term

ANOVA Notation … i

Individual

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• 50° room scores: 0, 1, 3, 1, 0

• 70° room scores: 4, 3, 6, 3, 4

• 90° room scores: 1, 2, 2, 0, 0

____________________________

(Example: In the 50° room, the score 3 is from person i = 3.)

• An Individual’s SPECIFIC SCORE

i = 3

ANOVA Notation … j

Treatment Condition / FACTOR

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• (1) 50° room scores: 0, 1, 3, 1, 0

• (2) 70° room scores: 4, 3, 6, 3, 4

• (3) 90° room scores: 1, 2, 2, 0, 0

____________________________

• Which Group the SCORE BELONGS TO

EXAMPLE)

j = 1 → 50° room

j = 2 → 70° room

j = 3 → 90° room

ANOVA Notation … k

Number of Treatment Conditions

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• (1) 50° room scores: 0, 1, 3, 1, 0

• (2) 70° room scores: 4, 3, 6, 3, 4

• (3) 90° room scores: 1, 2, 2, 0, 0

____________________________

• How MANY Groups TOTAL

EXAMPLE)

3 rooms TOTAL → k = 3

ANOVA Notation … n

Number of Scores in Each Treatment Condition

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• (1) 50° room scores: 0, 1, 3, 1, 0

• (2) 70° room scores: 4, 3, 6, 3, 4 → (5 people)

• (3) 90° room scores: 1, 2, 2, 0, 0

____________________________

• How MANY PEOPLE in Each Group

Each Room HAS 5 PEOPLE → n = 5

ANOVA Notation … N

Total Number of Scores In Entire Study … N = kn

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• (1) 50° room scores: 0, 1, 3, 1, 0

• (2) 70° room scores: 4, 3, 6, 3, 4 → (5 people)

• (3) 90° room scores: 1, 2, 2, 0, 0

15 Scores

____________________________

• All Scores … N = 3 × 5 = 15

ANOVA Notation … X_ij

“Individual Score”

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• (1) 50° room scores: 0, 1, 3, 1, 0

• (2) 70° room scores: 4, 3, 6, 3, 4 → (5 people)

• (3) 90° room scores: 1, 2, 2, 0, 0

15 Scores

____________________________

• Putting i and j next to each other (just a label)

EXAMPLE)

Person 5 in 90 Degree (group 3) room Scored 0 → X_53 = 0

• reads as “The score from individual 5 in condition 3 is 0” … X_53 = 0

ANOVA Notation … X̄_.j

Mean of a Treatment (Average Score for each j (room/group))

____________________________

Context Example

Factor: Room Temperature
Levels: 50°, 70°, 90°
Each room has 5 scores.

Sample data (same as lecture):

• (1) 50° room scores: 0, 1, 3, 1, 0

• (2) 70° room scores: 4, 3, 6, 3, 4 → (5 people)

• (3) 90° room scores: 1, 2, 2, 0, 0

15 Scores

____________________________

Example)

X̄_.1 (50 Degree room) = 1

X̄_.2 (70 Degree room) = 4

X̄_.3 (90 Degree room) = 1

ANOVA Notation … X̄_..

Mean(Average) of ALL Scores Combined … X̄_.. = 2 → same calc for OG Mean

ANOVA Notation … SS_Total Variability

How Much ALL Scores DIFFER from X̄_..

• Including STE & RUD

SS_TV = SS_Between + SS_Within

OR

SS_TV = ∑(X_ij -X̄_..)²

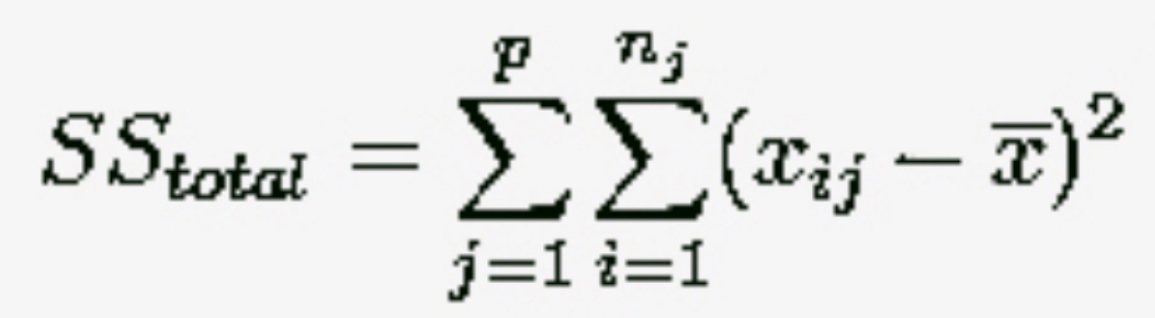
ANOVA Notation … SS_Between

Variability Between Treatments

SS_Between = n∑(X̄_.j - X̄_..)²

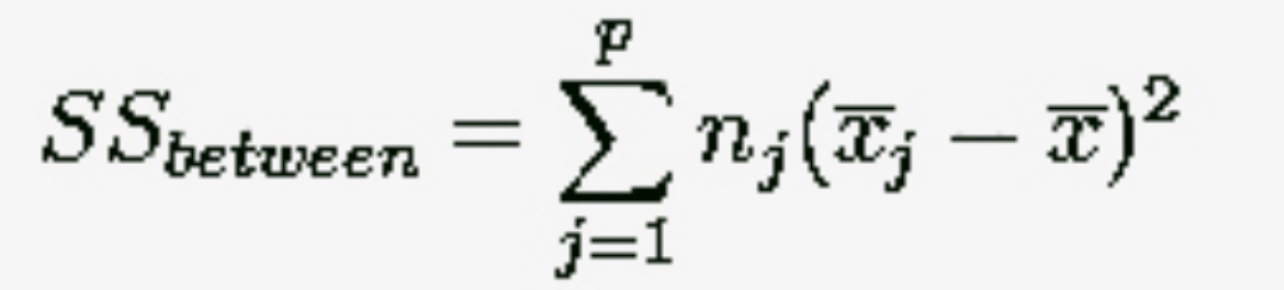
ANOVA Notation … SS_Within

Variability Within Treatments

SS_Within = ∑(X_ij - X̄_.j)²

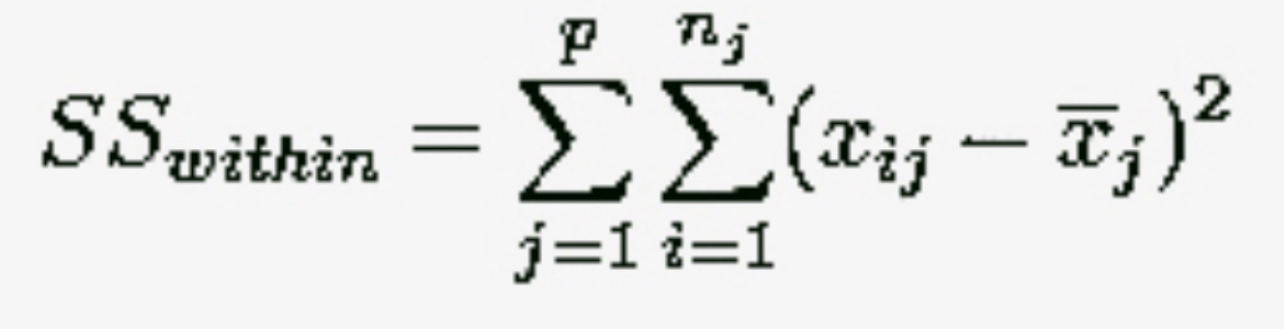
ANOVA Notation … df

dfbetween = k - 1

dfwithin = k(n -1)

dftotal = kn - 1 … N - 1 … dfbetween + dfwithin

Significant F Statisics

• Indicates NOT ALL Population Means are Equal

- μ ≠ μ

- omnibus test

• DOESN'T Say WHICH μ are DIFFERENT from each other

• Tests SPECIFIC HYPOTHESES … H_1

Planned & Unplanned Comparisons

POST-HOC Tests

• Additional Hypotheses Test

- conducted AFTER ANOVA

- Determine EXACTLY WHICH Mean Differences are Significant OR Not

PLANNED COMPARISONS

• SPECIFIC Mean Difference that are Relevant to SPECIFIC Hypotheses

- Researcher had in mind BEFORE STUDY was conducted

UNPLANNED COMPARISONS

• Making ALL POSSIBLE COMPARISONS

- Chance a Significant Differences will APPEAR

Controlling Error Rates Post Hoc Comparisons

• Type I Errors keep INCREASING when we make MULTIPLE COMPARISONS

FAMILYWISE ERROR RATE (FWR)

• FWR = 1(1 - α)^k-1

• PROBABILITY a Family of Conclusions will Contain at least ONE Type I Error

- Control this ERROR RATE

BONFERRONI α LEVEL

α = α/C

C ← TOTAL NUMBER of Mean Comparisons being Made