Topic 12: Gravitational Fields - Model Answers

1. Define gravitational field

A region where a mass experiences a force.

2. Define gravitational field strength.

The gravitational force per unit mass g = F/m.

3. Recall Newton’s Law of gravity.

• The attractive gravitational force that acts between two masses is directly proportional to the product of their masses, and inversely proportional to the square of the distance between their centres.

• The force that acts between two masses, m₁ and m₂, whose centres are separated by a distance of r is given by: F = - Gm₁m₂ / r²

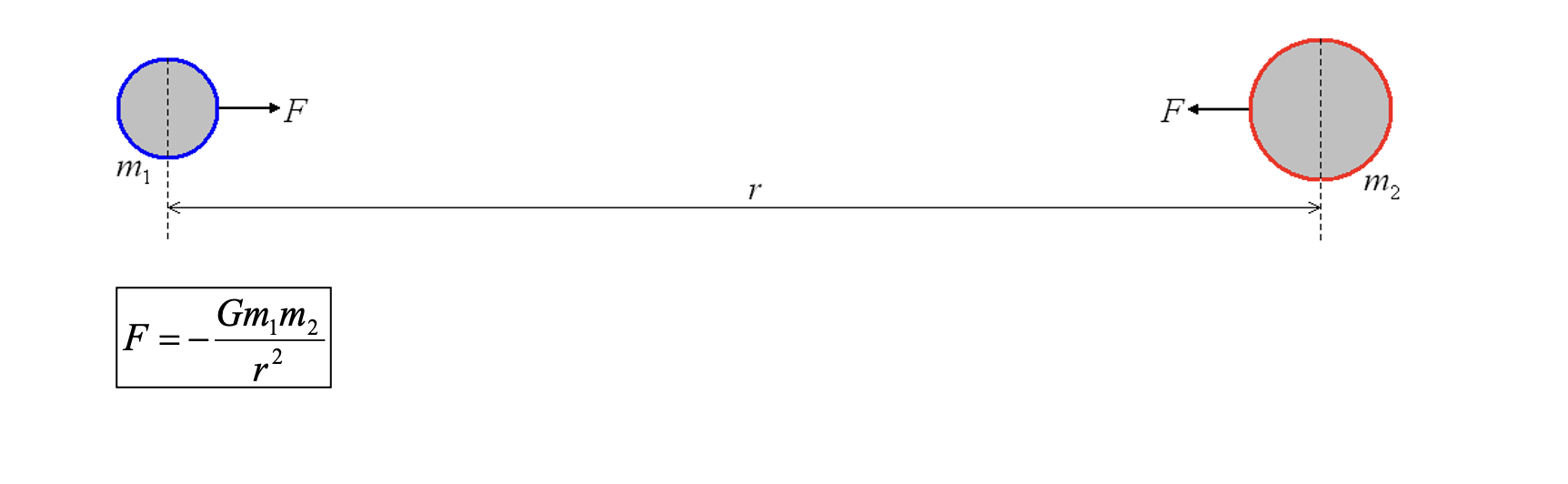
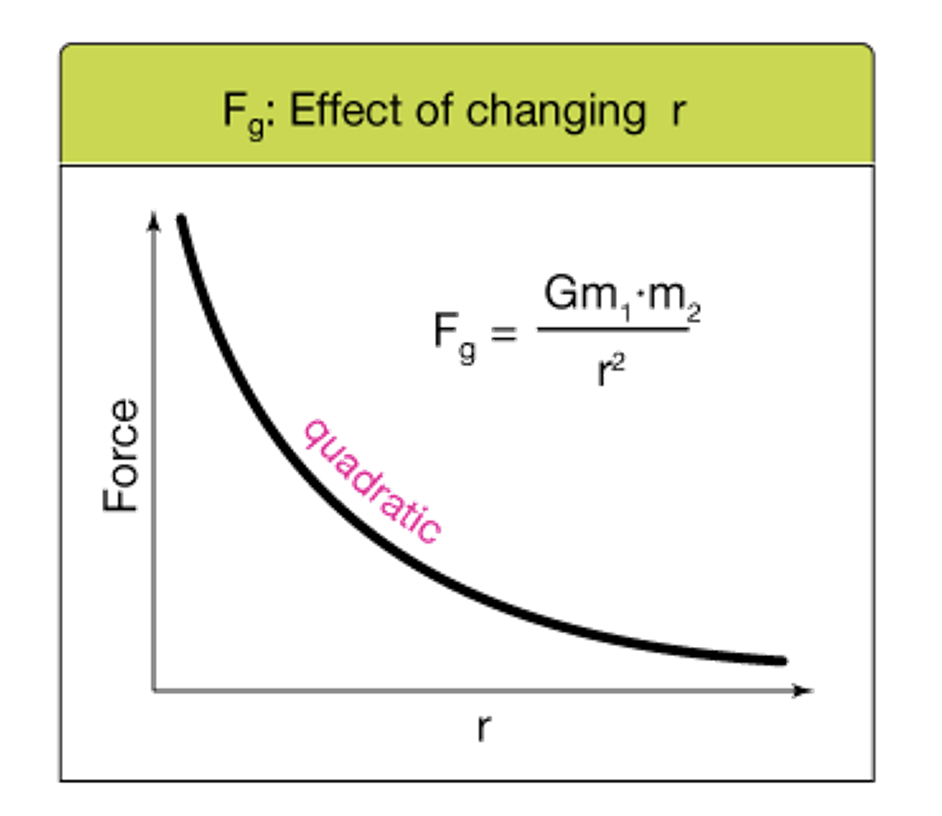
4. Explain what an inverse square law relationship between force and distance means and how to prove it using data.

• The inverse square law relationship means that force is proportional to 1/r²

• Ways to prove this:

1. Plot a graph of F against 1/r² - should be a straight line through the origin.

2. Plot a graph of F against ln r - should be a straight line with gradient -2.

3. From data, calculate three seperate values of Fr² - all of these should equal the same constant, k.

4. From data, determine the values of r when F doubles (do this at least 3 times). Identify whether r is increased by a factor of 4.

5. Sketch a graph of F against r, as you move away from a point mass.

(Inversely proportional graph)

6. Describe what gravitational field lines show.

The field lines show the direction, that a mass in a gravitational field would experience a force.

7. Draw the field lines for the Earth as seen from a distance, and close up.

Distance: radial field

Close up: uniform field.

ALWAYS towards Earth.

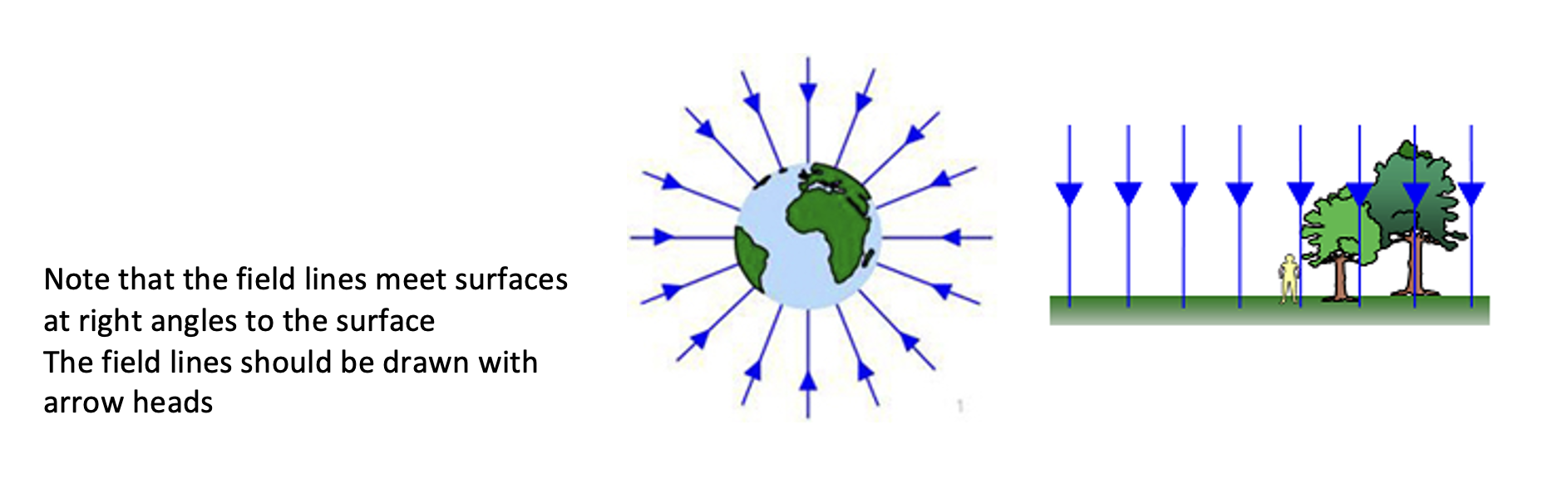
8. Describe what is meant by a uniform field.

• A uniform field is one in which the gravitational field strength is constant everywhere.

• The field lines are parallel in a uniform field.

9. Describe what is meant by a radial field.

• A radial field is one in which the field obeys an inverse square law.

• The gravitational field strength decreases with the inverse square of the distance, from the centre of the mass.

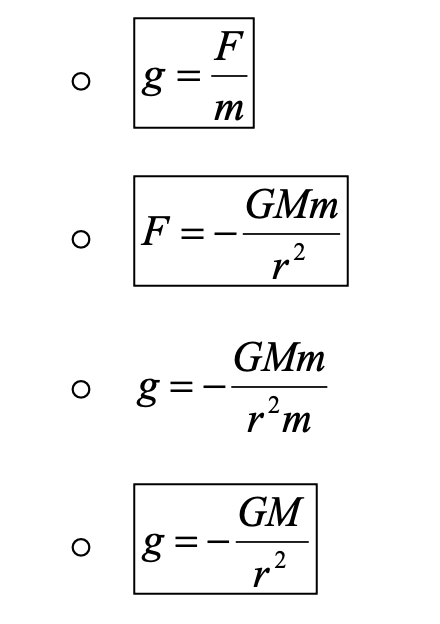
10. Derive the equaltion for gravitational field strength a disthce r away from a body of mass, M.

Start with g= F/m

Plug in formula for F (remember -ve)

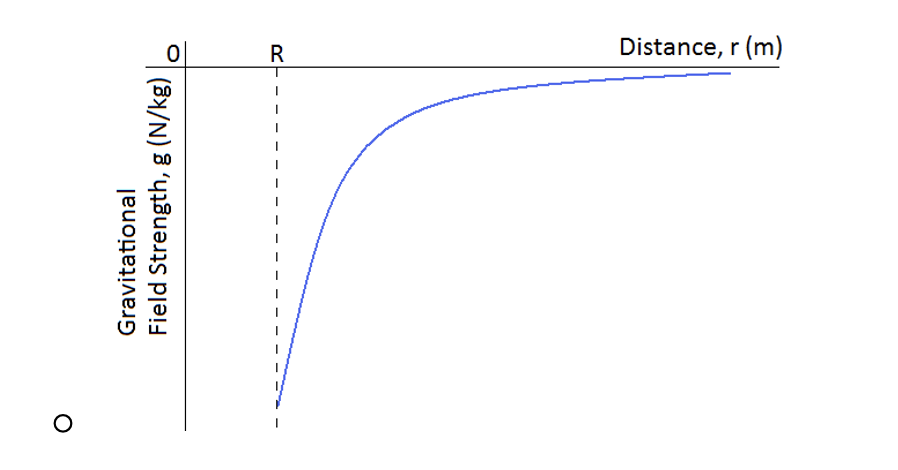
11. Sketch a graph of the gravitational field strength against distance from the centre of a mass of radius, R.

(g is proportional to -1/r²)

12. Explain why the mass of the orbiting body (e.g.Earth around the Sun or Moon around the Earth) has no effect on the gravitational field strength - link to the equation.

• g = -GM/r² is the equation for gravitational field strength - the gravitational force per unit maths.

• M is the mass of the gravitational field creator

• In the gravitational field strength definition, it is the force per unit mass, so the mass of the orbiting body is irrelevant as it does not appear in the equation.

13. Define centripetal force and explain where it comes from in gravitational fields.

• The centripetal force is the resultant force that acts towards the centre of a circle when an object moves in a circle.

• In gravitational fields, the centripetal force is provided by the gravitational force.

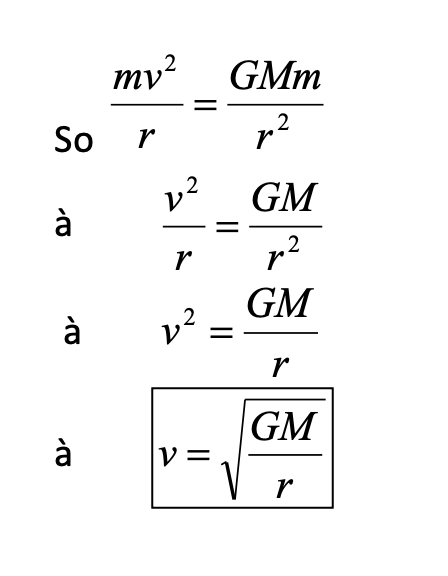
14. Link the cenrtipetal force to gravitational force for objects in orbit, and hence derive the relationship between orbital velovity and radius of orbit.

• F = GMm / r² is the gravitational force acting on an object and is the resultant force.

• If the object is in circular motion, this resultant force is equal to the centripetal force F = mv² /r .

• …

15. Explain why fast moving distant objects (e.g. distant comets) will not move in circular motion around the Earth.

• The gravitational force is low when an object is far away from the Earth, as F = Mm/r² so when r is high, F is low.

• The required centripetal force for circular motion, is high F = mv²/r as v is very high.

• Therefore, the gravitational force is not high enough to provide the required centripetal force as F = mv²/r for circular motion.

16. Explain why the mass of the orbiting body has no effect on its orbital velocity.

• The orbital velocity of an orbiting body is v = Root(GM/r).

• Therefore the velocity only depends on the distance, r from the centre of the field creating mass, the mass M of the field creating mass, and the gravitational constantly.

17. Explain what happens when the orbital velocity as an objects’ radius orbit increases.

• The orbital velocity decreases as radius r increases.

• Orbital velovity is proportional to the inverse square root of the radius of orbit.

18. Link the centripetal force to gravitational force for objects in orbit and hence derive the relationship between radius and time period (Kepler’s Law).

• F = GMm / r² is the resultant force

• If this object is in circular motion, this resultant force is equal to the centripetal force, F = mrω²

• so …

• (remember ω = 2π/T)

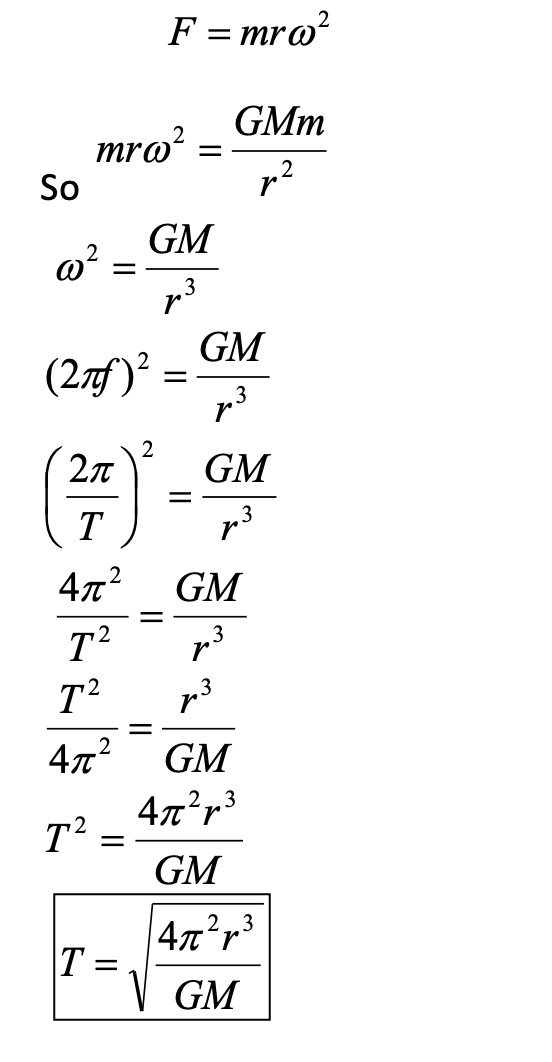
19. Describe how a change in radius affects the time period.

• As the radius increases, the time period increases

• The time period squared is proportional to the radius cubed.

20. Describe key differences and similarities between electric and gravitational fields.

• Gravitational fields are regions in which a mass experiences a force due to its mass.

• Electric fields are regions in which a charge experiences a force due to its charge.

• Both types of field have an infinite range.

• In each type of field, the force varies as an inverse square.

• The force between masses is always attractive whereas the force between charges can be attractive or repulsive.

• The force between charges at any given separation is much stronger than the force between masses at the same separation.

21. Define gravitational potential.

The work done per unit mass against the field to move a point mass from infinity to that point.

22. State the equation for the gravitational potential at a distance r from a mass, M.

The gravitational potential at a distance r from mass M is give by: (always negative)

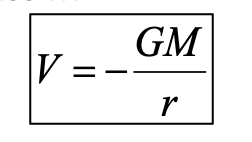
23. Explain why the gravitational potential is negative for gravitational fields.

• The value is negative because the potential at infinity is zero and as we move towards the mass, the potential or energy decreases.

• The gravitational field is attractive so work is done by the field in moving the mass, meaning energy is given out.

24. State the units of gravitational potential.

Gravitational Potential, V_grav is measured in Jules per kilogram, J kg^-1

25. Is gravitational potential a scalar or a vector?

Scalar

26. Explain how to calculate the gravitational potential due to multiple bodies.

• Separately calculate the value of the gravitational potential due to each body using V = -GM/r.

• Add each value up to calculate the total potential.

27. Sketch the graph of gravitational potential against r for a body of radius R.

(Negative recipracol graph)

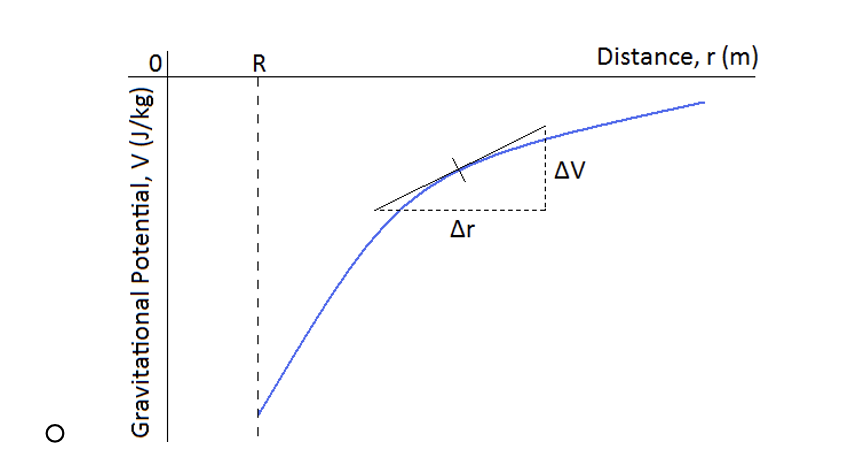
28. Explain how to determine the gravitational field strength from a potential, distance graph (V,r graph).

The gradient of the gravitational potential graph gives us the gravitational field strength at that point. To find the gradient at a point on a curve, we must draw a tangent to the line then calculate the gradient of the tangent.

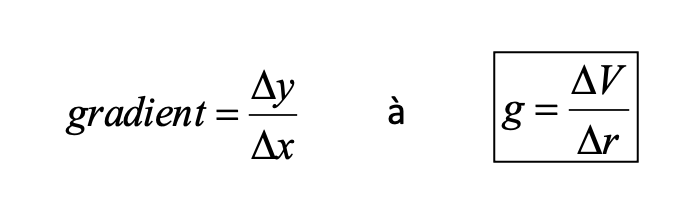
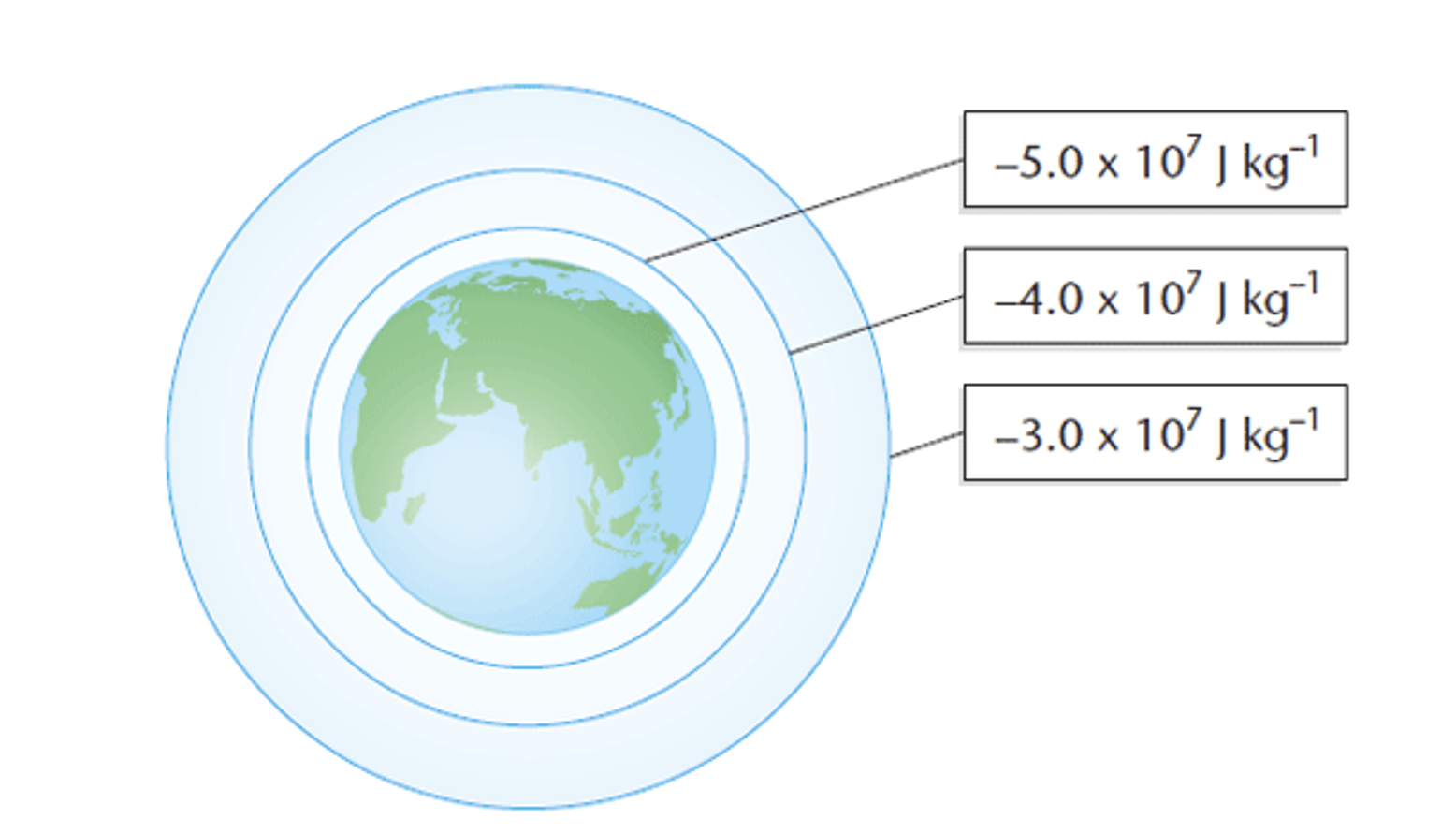
29. Draw equipotential surfaces around the earth.

(Rings get further apart)

30. Explain the differejce bewteen gravitational potential and gravitational potential energy.

• Gravitational potential energy is the work done against the field to move a point mass from infinity to that point.

• Gravitational potential is the work done per unit mass against the field to move a point mass from infinity to that point.

(potential is for per unit mass only)

31. Explain how to calculate the GPE gained in moving a mass between equipotential surfaces.

• ∆GPE = m∆V

• Calculate the change in potential ∆V and then multiply this by the mass that you are moving bewteen the surfaces.

• If you are given values of V, it is simple: ∆V = V₂ - V₁

• If you are not given any values, you need to calculate each value of the potential:

• V₁ = -GM/r₁ and V₂ = -GM/r₂

• The subtract ∆V = V₂ - V₁ as above.

32. A student uses the equation ∆GPE = mg∆h to calculate the change in gravitational potential energy as a mass is moved from the Earth to a satellite 500km above the Earth’s surface. a) Explain why this is the wrong approach. b) Explain when ∆GPE = mg∆h can be used.

• This is the wrong approach because the gravitational field strength, g, is not constant across that 500km distance.

• g = -GM/r² and so this decreases with the inverse square of distance from the centre of the mass

• Instead, ∆GPE = m∆V should be used, where ∆V is the change of potential between the Earth’s surface and the satellite.

• ∆GPE = mg∆h can only be used in the region where g is approximately constant - ie. close to the Earth’s surface.

33. Derive the expression for the total energy of a body in orbit.

1. Total energy = Kinetic energy + Potential energy (or E_T = E_k + E_p)

Inbetween steps get v² = GM/r from using F_centripetal = F_{gravitational} where the centripetal force = mv²/r.

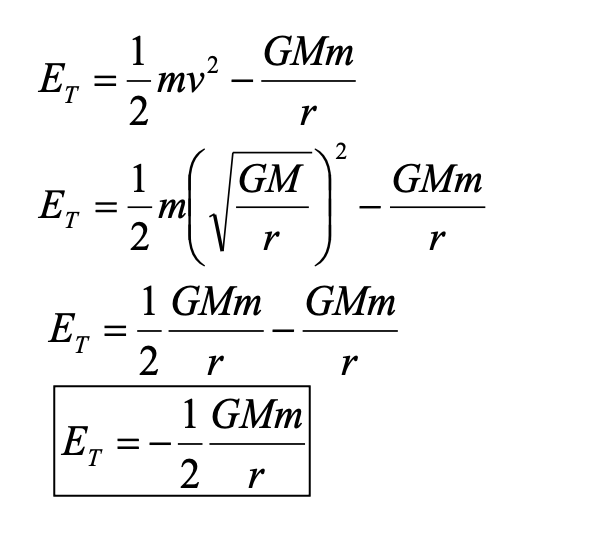
34. Explain what happens to an object’s kinetic energy as its radius of orbit increases.

• As the radius of the orbit increases, the kinetic energy would decrease, as kinetic energy = ½ mv² = ½ m x GM/r

• So as r increases, kinetic energy decreases.

• This is because kinetic energy is transferred into gravitational potential energy.

35. Derive the equation for escape velocity. Explaining each step.

For an object to be thrown from the surface of a planet and esape the gravitational field (to infinity), the initial kinetic energy it has at the surface, must be equal to the potential energy (work done) to take it from the surface to infinity. All of the kinetic energy is transferred to potential energy in its journey.

36. Explain what is menat by ‘weighhtlessness’.

• Weightlessness is when an object only experiences weight.

• An object standing on the ground would ‘feel’ the normal contact reaction force pushing them upwards.

• When the normal contact froce is zero, the object does not ‘feel’ a push upwards, and this is described as the sensation of ‘weightlessness’

• (reaction/normal contact frocelessness)

37. Explain why a person on a rollercoaster ride that falls with an acceleration of g feels ‘weightless’.

• When the ride and person falls down at g, they must experience a resultant force F = ma = mg due to Newton’s secodn law.

• Therefore the only force acting on them must be weight = mg.

38. Explain why we feel heavier when we are in a lift that is accelerating upwards at 0.2 ms^-2.

• When we are accelerating upwards at 0.2 ms^-2, the resultant force acting on us must be F = ma = 0.2m by Newton’s second law.

• The resultant force in this situation woruld be R - W, where R is the normal contact froce upwards and W is the weight downwards.

• So F_R = R - W = 0.2m

• So R = 0,2m + W

• In other words, the normal contact reaction force is higher than when the object is stationary, where the resultant force would be zero and reaction force would equal weight.

• As we ‘feel’ the reaction force acting on us, we should therefore ‘ feel’ heavier even though our weight is the same.