Stats Unit 1 Vocab

Individual

An object described in a set of data.

Variable

A attribute that can take dif. values for dif. individuals

Categorical Variable

Assigns labels that place individuals into a specific group called category

Quantitative Variable

Takes # values (quantities) ex. counts, measures, age

Discrete Vriaable

A quantitative variable that takes a fixed set of possible values w/ gaps between them. (ex. 1 - 2 - 3)

Continuous Variable

A quantitative variable that can take any value in an interval on the number line (ex. 0- infinity)

Distribution

Tells us what values the variable takes and how often

Frequency Table

shows # of individuals having each value

Relative Frequency Table

shows proportion/percent of individuals having each value

Bar Graph

shows each category as a bar, heights of bars show category frequencies/relative frequencies

Pie Chart

shows each category as a slice of a pie. Areas of slices are proportional to category frequencies/relative frequencies

Two-way-Table

Table of counts that summarizes data on the relationship between two categorical variable for some group of individuals.

Marginal Relative Frequency

Gives the %/proportion of individuals that have a specific value for one categorical variable. (tells you only about one of the variables in a two-way table)

Joint Relative Frequency

Gives the %/proportion of individuals w/ specific values for two categorical variables.

Conditional Relative Frequency

Gives the proportion of individuals that has a specific value for one categorical variable among individuals who share the same value of another categorical variable (the condition).

Association

There is association between two variable if knowing value of one, helps predict the other.

Graphs

Use a side by side bar graph, a segmented bar graph or a mosaic plot to compare the distribution of a categorical variable for two or more groups.

Dotplot

Show each data value as a dot above its location on a #-line

Symmetric Distribution

right side of dot plot = roughly a mirrored version on the left

Skewed Right

Right side is much longer and has less values

Skewed Left

Left side has less values and is much longer

Graph Shape

Ex. The distribution is skewed right with a single peak at 1 goal. There is a gap between 5 and 9.

Outliers

An observation that falls outside of the overall pattern. Ex. Games where 9&10 goals were scored appear to be outliers.

Center

The median is 2 goals scored.

Variability

The data vary from 1 to 10 goals scored.

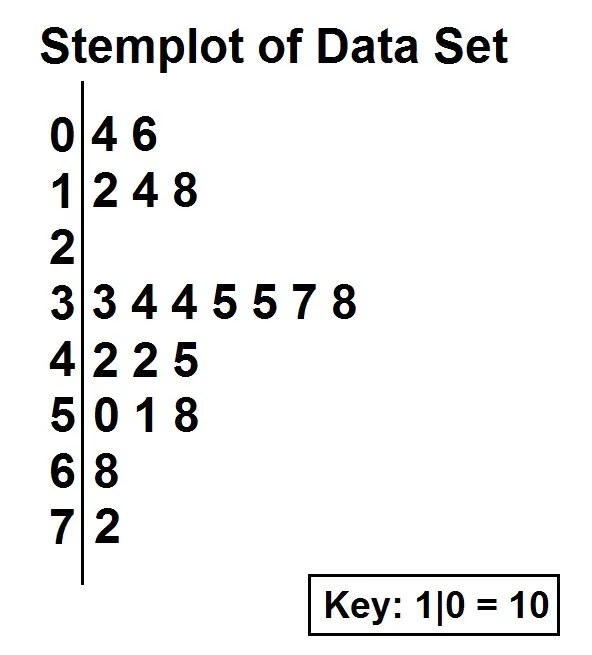
Stemplot

shows each data value separated into two parts.

A stem: consisted of all but the final digit

A Leaf: the final digit

Stems are ordered from lowest to highest in a vertical column

Leaves are ordered from smallest to largest number from the appropriate stems

Histograms

Shows each interval of values as a bar.

Heights of bars show the frequencies or relative frequencies of value in each interval.

Mean

The average of all the individual data values.

Statistic

A # that describes some characteristic of a sample.

Parameter

A # that describes some characteristic of a population.

Resistant

A statistical measure is resistant if it isn’t sensitive to extreme values.

Median

The midpoint of a distribution, half the observations are smaller, half are larger.

Comparing mean and median

Mean < Median : skewed left

Mean = Median : Roughly Symmetric

Mean > Median : skewed right

Range

The distance between the min. & max. value

Range = max - min

Ex. The data varies from 1 to 10 with a range of 9.

St. dev

measures the typical distance of values in a distribution from the mean

• always greater of equal to 0

• 0 when all values in a dsitrubtion = same

• increases with increased variation from mean

• measures variation about the mean

St dev formula

( value - mean)² = variance

square root variance = st. dev

Quartiles

the values that divide the distribution into 4 groups of roughly equal size. Arrange data least to greatest to find.

1st Quartile

the median of the data values that are left of the median

3rd Quartile

The median of the data values to the right of the median

IQR (interquartile range)

measures the variability in the middle half of the distribution

the distance between the 1st and 3rd quartiles of a distribution

IQR = Q₃ - Q₁

How to identify outliers

If it falls more than 1.5 x IQR above the 3rd or below the 1st quartile

Low Outliers < Q₁ - (1.5 x IQR)

High Outliers > Q₃ - (1.5 x IQR)

5 Number Summary

The 5 #;s of a distribution of quantitative data consists of the

minimum, Q₁, median, Q₃, maximum

Boxplot

A visual representation of the 5 # summary