AP Calc Unit 10 Study Guide

What is a monotonic sequence?

A sequence that constantly increases or constantly decreases

What is a convergent series?

A series with a partial sum that converges to a value as n approaches infinity.

What is a geometric sequence?

A sequence where the same number is multiplied to each term to get the next in the sequence.

When and where does a geometric series converge?

When the absolute value of r is less than 1, the series converges to a÷(1-r) where a is the first term.

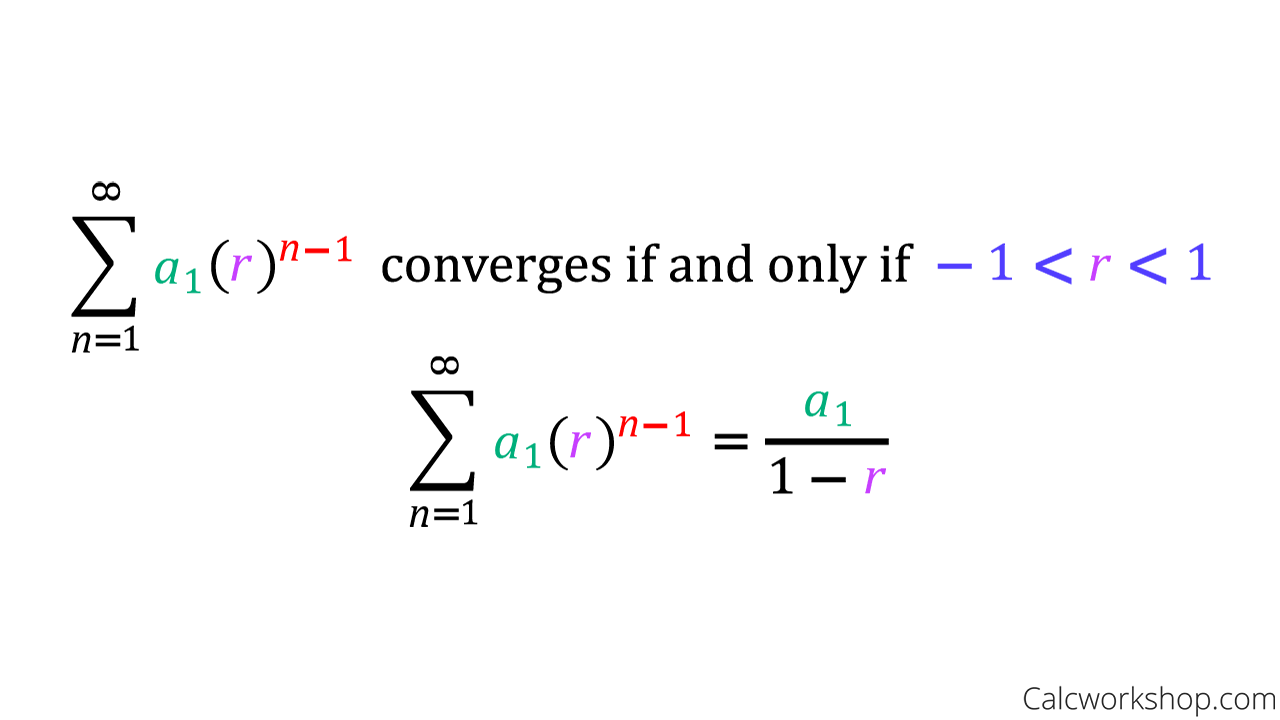
What is the nth term test for divergence?

If the limit of the nth term of a series as n approaches infinity doesn’t equal to 0, the series diverges.

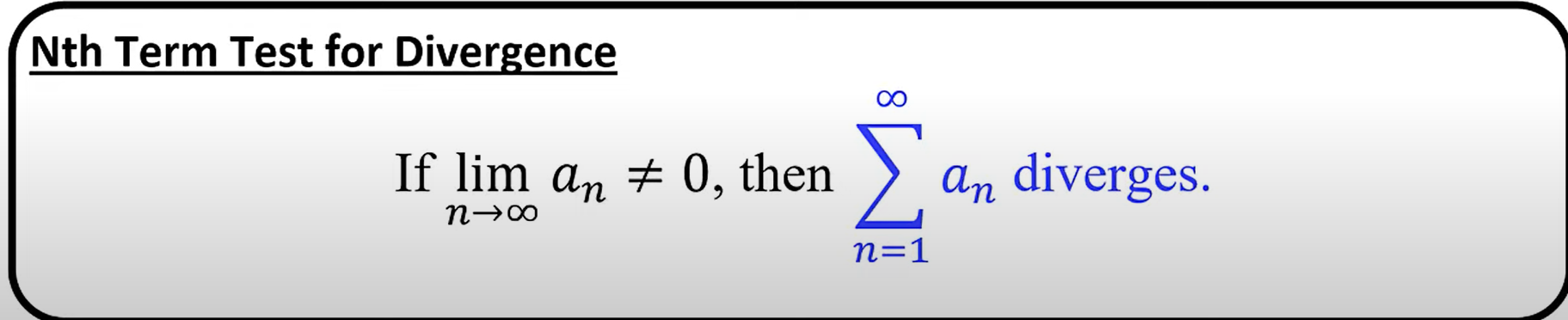
What is the integral test for convergence?

If f is a positive, continuous, and decreasing function for x ≥ k and a_n = f(x), then the sum of all terms in the series starting from n = k and the integral from k to infinity of f(x) both converge or both diverge.

When does a p series converge or diverge?

Converges if p > 1

Diverges if 0 < p ≤ 1

Do harmonic series converge or diverge?

Always diverge

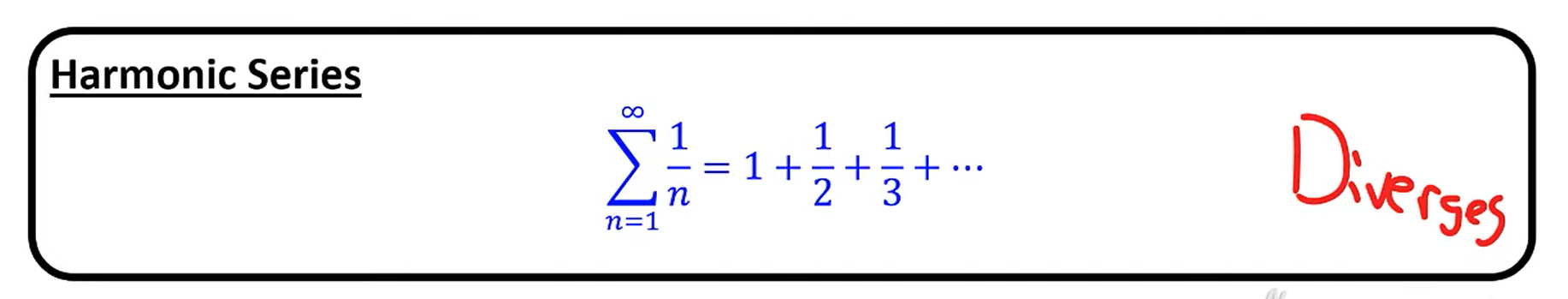
What is the comparison test for convergence?

If 0 < a_n ≤ b_n for all n, then if the partial sum of b converges, the partial sum of a must converge. If the partial sum of a diverges, the partial sum of b must diverge.

What is the Limit Comparison Test?

If both a_n and b_n are greater than 0 and the limit of a_n divided by b_n as n approaches infinity is finite and positive, then the partial sums of a and b either both converge or both diverge.

What is the Alternating Series Test?

If a_n > 0, the limit as n approaches infinity of a_n = 0, and |a_n+1| ≤ |a_n| for all n, then the alternating series must converge. Otherwise, it must diverge.

What is the Ratio Test for Convergence?

If an infinite series a_n has positive terms, then if the limit of a_n+1 divided by a_n as n approaches infinity is less than 1, the series converges. If it is greater than 1, the series diverges. If it equals 1, then you must use another test.

What is absolute and conditional convergence?

If the absolute value of a series converges, the original series must converge absolutely. If it instead diverges, the original series can either converge (converges conditionally) or both diverge (divergent).

What is the error bound for a converging alternating series?

The absolute value of the remainder (sum of the series - a partial sum to term n) must be less than or equal to the absolute value of term n + 1.

What is the difference between a Taylor polynomial and a Maclaurin polynomial?

A Maclaurin polynomial is a Taylor polynomial centered at x = 0.

What is the formula for an Nth Taylor polynomial or a Maclaurin polynomial?

What is the formula for the coefficient of an nth degree term in a Taylor polynomial centered at x = c ?

What is the formula for a Lagrange Error Bound?

What are the ways that a power series can converge?

1. Converges to an interval

   1. The radius is the distance from the center to the edge of the interval

2. Converges to all real numbers

3. Converges only to the center (x = c)

What is the Ratio Test for Interval of Convergence?

If the limit of the absolute value of a_n+1 divided by a_n is…:

• Less than 1: Converges to an interval

• Equal to 0: Converges for all real values of x

• Equal to infinity: Converges only to the center

What is a Taylor series?

The series that is equal to the function for many common functions.

What is the Taylor series for e^x?

What is the Taylor series for sin(x)?

Odd coefficients

What is the Taylor series for cos(x)?

Even coefficients

What is the Taylor series for 1/1+x?