Calc 2 Test 1 Memorization

∫sinx dx?

-cosx + C

∫cosx dx?

sinx + C

∫csc(x) dx?

ln |cscx-cotx| + C

∫csc^2(x) dx?

-cotx + c

∫sec(x)tan(x) dx?

secx + C

∫csc(x)cot(x) dx?

-cscx + C

∫(e^x) dx?

e^x + C

∫1/√(x^2+1) dx?

tan^-1(x) + C

∫1/√(x^2-1) dx?

sin^-1(x) + C

∫secx dx?

ln|sec(x)+tan(x)| + C

∫tanx dx?

ln|secx| + C

∫cotx dx?

ln|sinx| + C

∫e^-x dx?

-1/e^x + C

What does ln(1) = ?

0

ln(0) = ?

infinity

How to know when you have to do IBP?

If you can't u-sub and the integral has 2 functions that don't simplify into 1, ex: ∫(e^x)(sin(2x))dx

What is the integration by parts formula?

∫u dv = uv - ∫v du

When doing trig integration what do you do if there's an odd power of sine or cosine (ex: sin^3(x))?

Break off one factor (ex: sin(x)), then convert the rest using a pythagorean identity (like sin^2(x) + cos^2(x)= 1), then u-sub

goal: reduce power to get something like u^n du

When doing trig integration what do you do if both powers are even?

use power-reducing identities to rewrite everything in terms of cos(2x) or sin(2x) then u-sub

goal: create an integral with no powers

When doing trig integration what do you do if you see tan or sec (or cot and csc)?

look to use identities like tan^2(x)+1=sex^2(x), then save a factor like sec^2(x) or sec(x)tan(x) to help you u-sub

goal: turn integral into something like ∫u^n du

Tips for trig integration

1. Always check if du matches part of the integral (to u-sub instantly)

if not..

2. Try rewriting powers with identities

3. Try pulling out a factor like sinx or sec^2(x)

Trig integration summary of what to do table

The 3 different cases for trig sub:

Look for these if you can't just u-sub

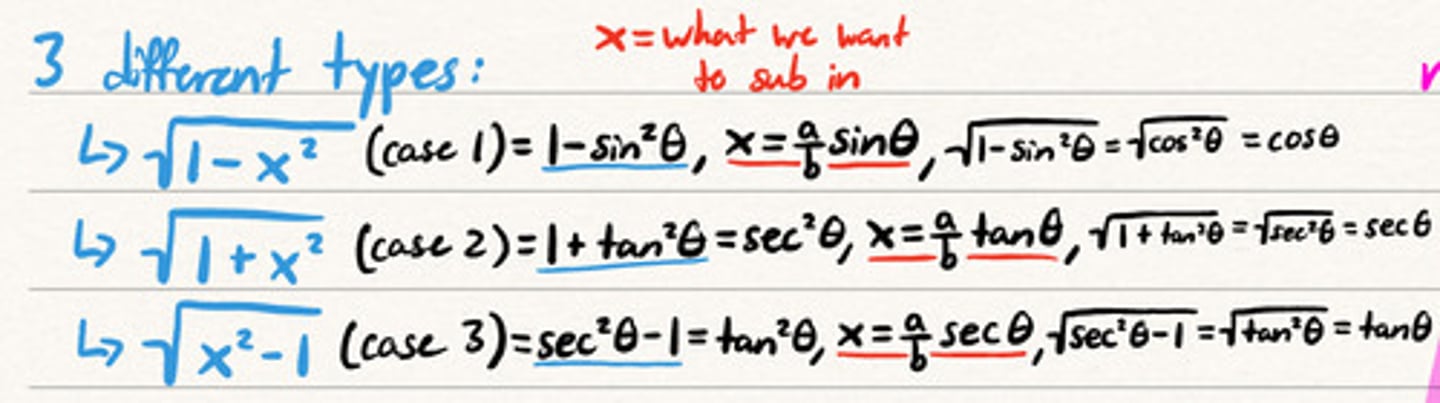
When doing trig sub and converting back to x from trig(theta) does the trig disappear or stay?

Disappear! Instead of tan(x/3) it should be x/3

Memorize the forms for partial integration:

For partial integration what format will your answer be in if your integral looks something like ∫1/(x-a) dx?

A ln |x-a| + C

For partial integration what format will your answer be in if your integral looks something like ∫1/(x^2+a^2) dx?

1/a arctan(x/a) + C

this is on your formula sheet, but it is good to know that this typically happens with irreducible quadratics with a constant numerator

The 1st type of improper integral (infinite bounds):

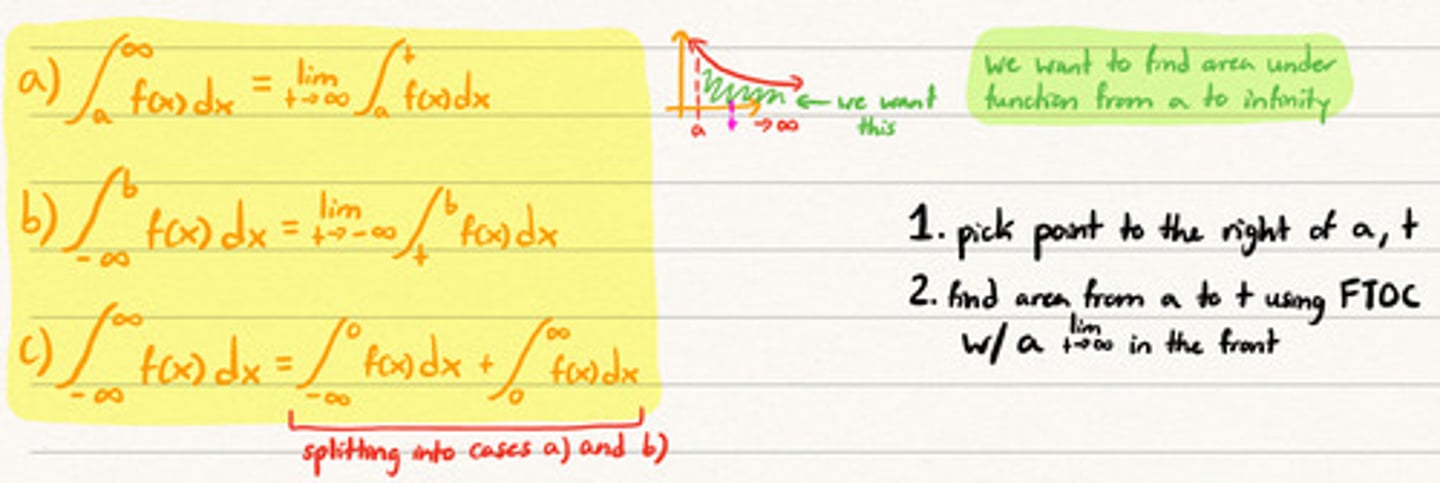
The 2nd type of improper integral (non-continuous):

If your answers looks something like: 1/3 + infinity does the limit converge or diverge?

diverge

What is it called when a limit exists? (ex: your answer is 2/3)

converge

Does anything you get in indeterminate form (ex 0-0) converge or diverge?

diverge

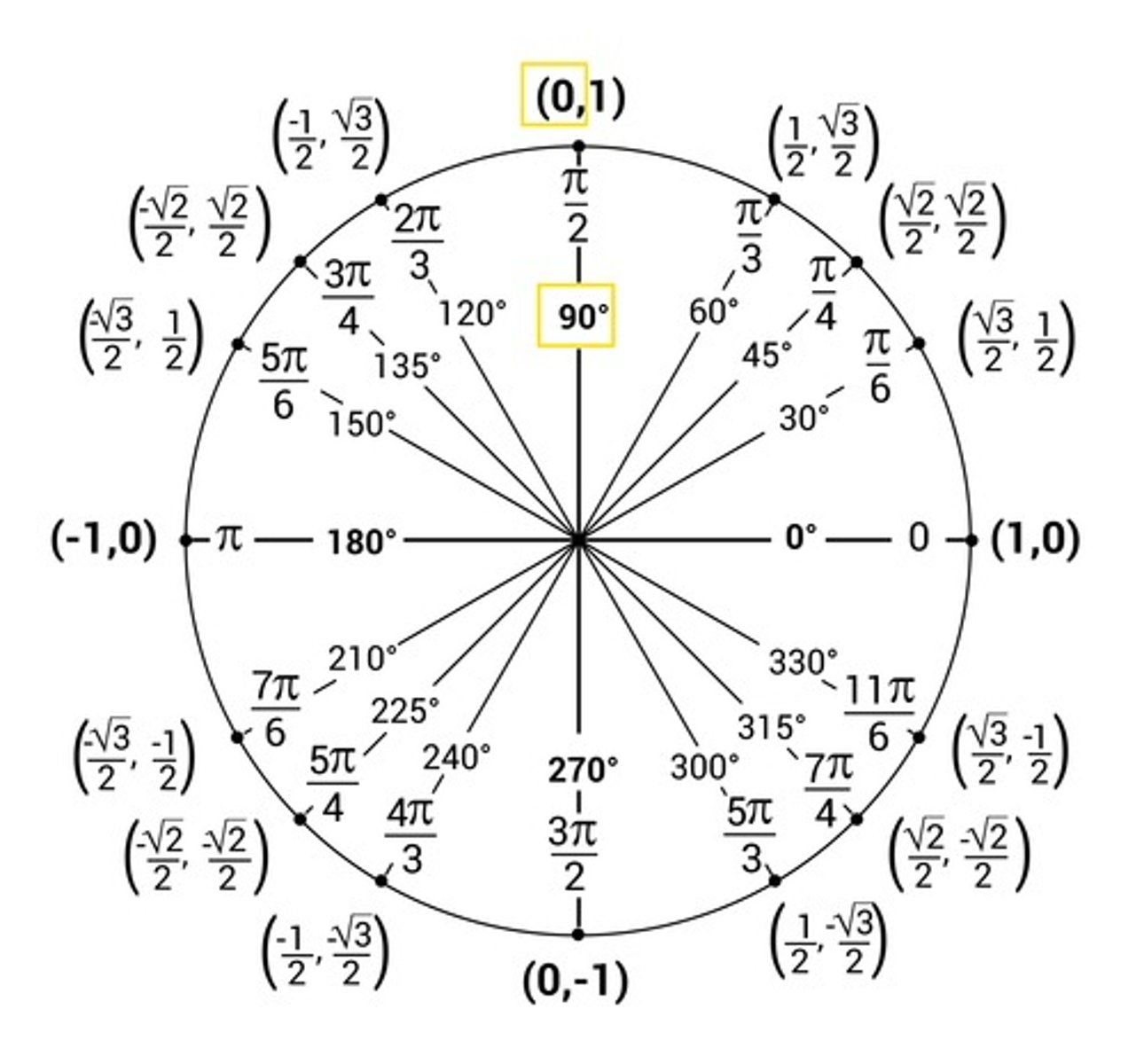
Know unit circle (for trig int):

When solving an indefinite integral make sure you don't forget to add....

+ C