12-01: Rates of Change

Rates of Change & The Slope of a Curve

Rate of change: the change in one quantity (dependent variable) with respect to another quantity (independent variable)

Slope = ∆y/∆x = (y2 - y1)/(x2-x1)

Rates of change are obtained this way

• Independent variables: are picked and can be controlled, e.g. time
• Dependent variables: depend on the independent variables, are an outcome

AROC - average rate of change: rate of change over an interval, between 2 points → corresponds to the slope of the secant line

IROC - instantaneous rate of change: rate of change at an instance, at a single point → corresponds to the slope of the tangent line

Find IROC from a table of values

Proceeding and Following method:

1. Look at the data that proceeds (comes before) and follows (comes after) the target data
2. Find AROC: (y2-y1)/(x2-x1)

Rates of Change Using Equations

Slope = ∆y/∆x = (y2 - y1)/(x2-x1)

can be written as

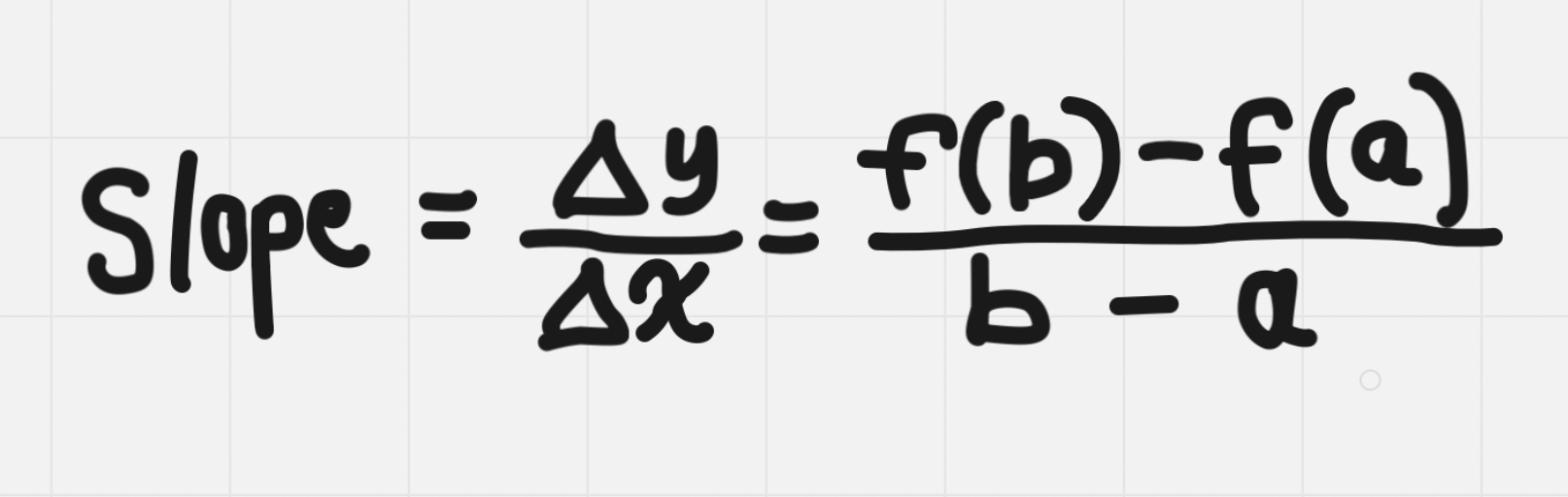
Difference Quotient - use for IROC

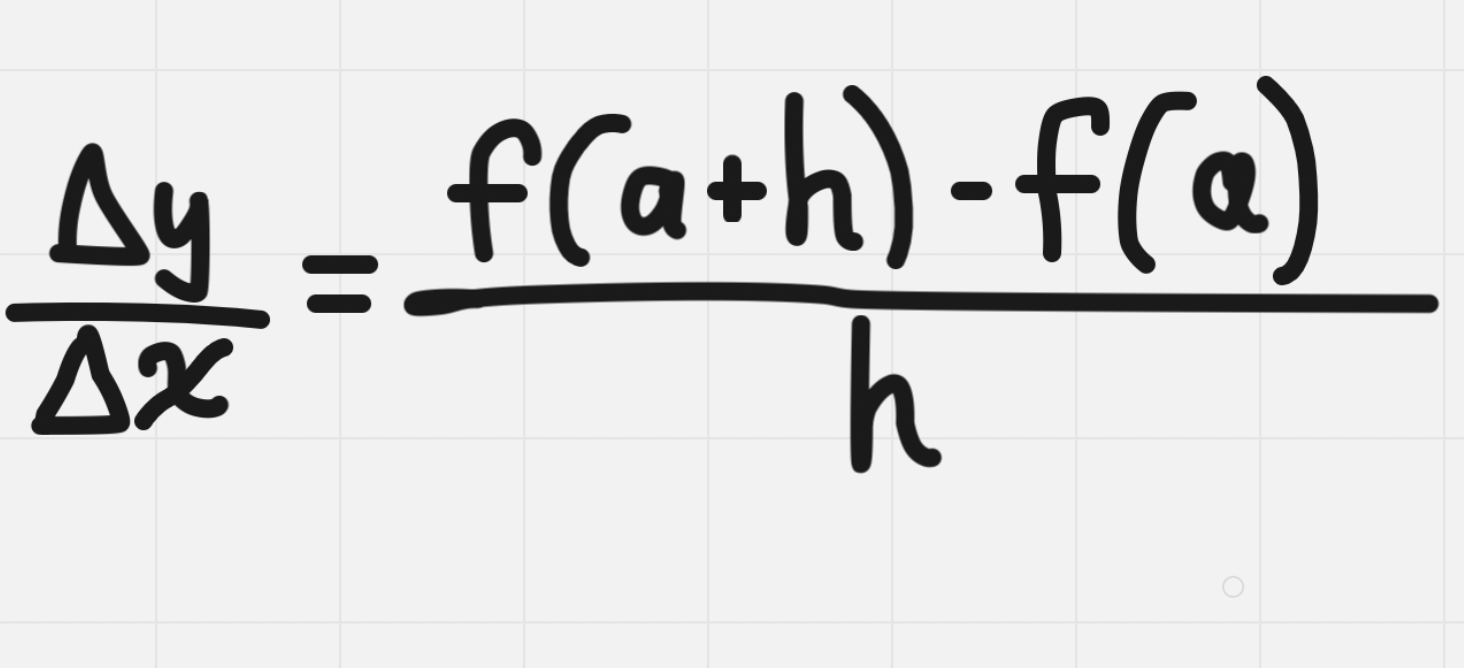
The closer h is to zero, the more accurate the estimate becomes

Limits

Using limits, the interval can be made infinitely small, approaching 0. As this happens, the slope of the secant line approaches its limiting value: the slope of the tangent line

• Gets closer to tangent as the secant numbers get smaller

Left hand limits: use values that are less than or to the left side of the value being approached

Right hand limits: use values that are greater than or to the right side of the right side of the value being approached

A limit is a boundary placed, saying that no matter how close it tries, it will never be equal to a

This is represented as

The limit exists if the following 3 criteria are met:

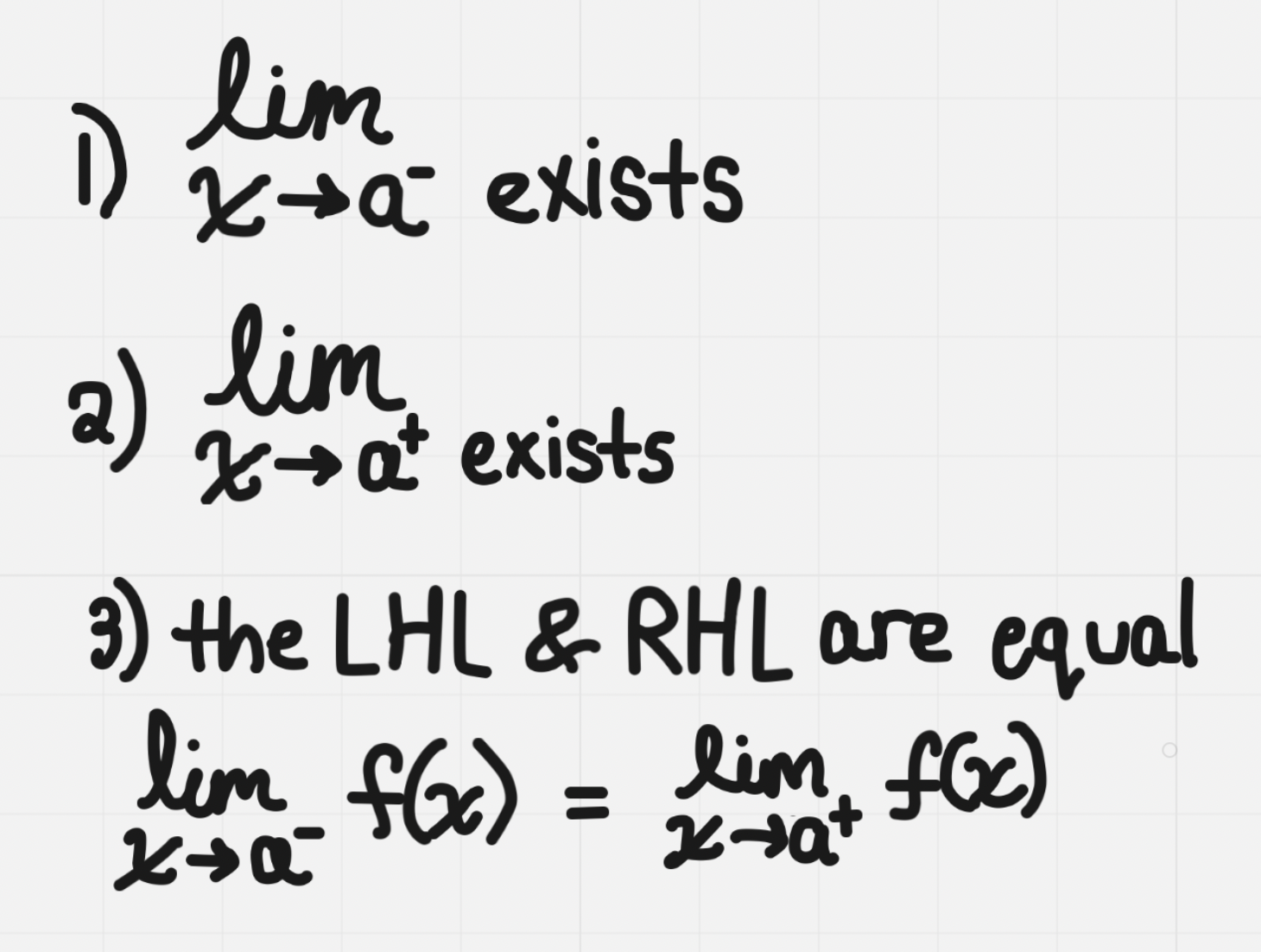
Continuous Functions

Continuous function: a function that is continuous at x for all values of xER

A function, f(x) is continuous at x=a if:

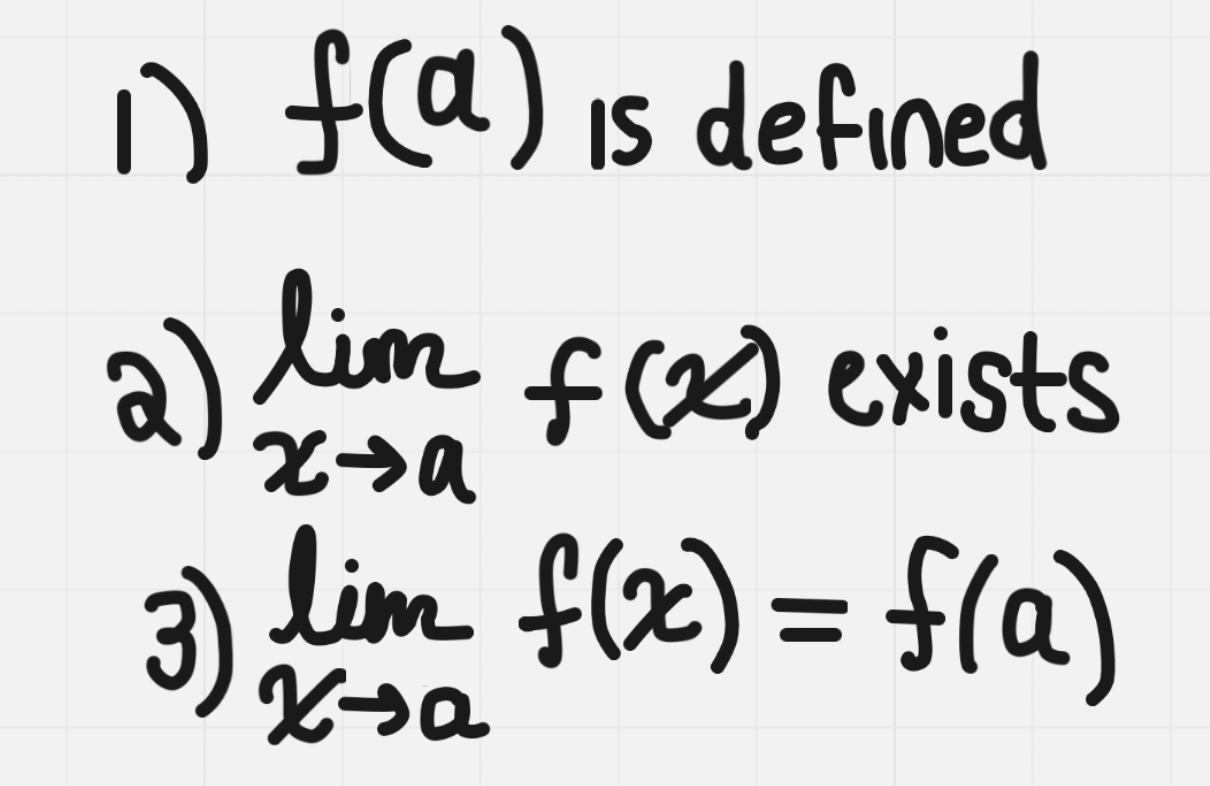
• A function is continuous if you can draw its graph without lifting your pencil
  • Holes, asymptotes, gaps mean that the it is discontinuous or has discontinuity at the point at which the gap occurs

Piecewise function: a function made up of 2 or more functions, each corresponding to a specific interval within the entire domain (each graph has its own domain). These are also discontinuous

Types of Discontinuity

Removable discontinuity: Hole (when factor cancels in equation). Function is undefined at a particular point

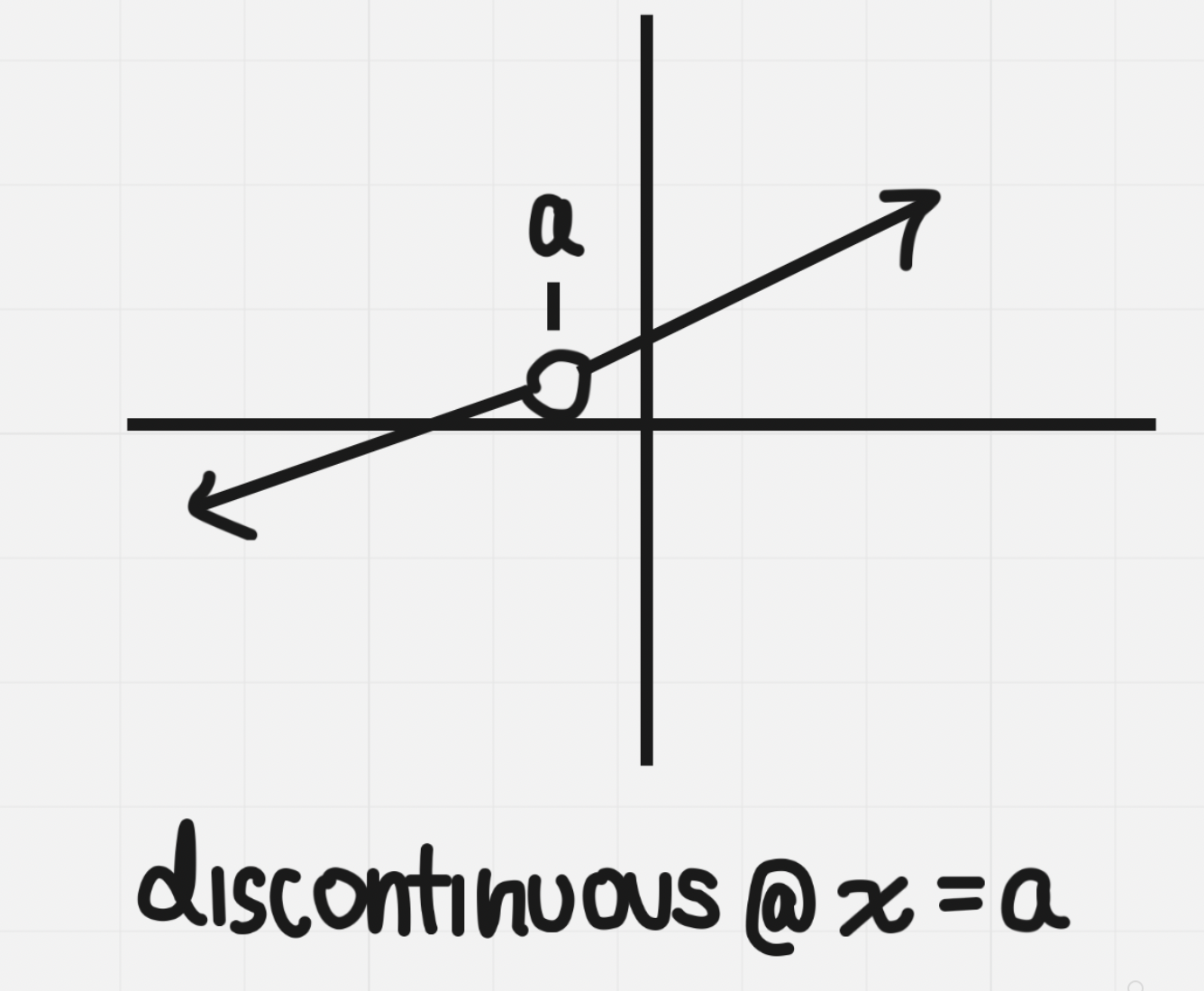
Jump discontinuity: One sided limits exist but are not equal

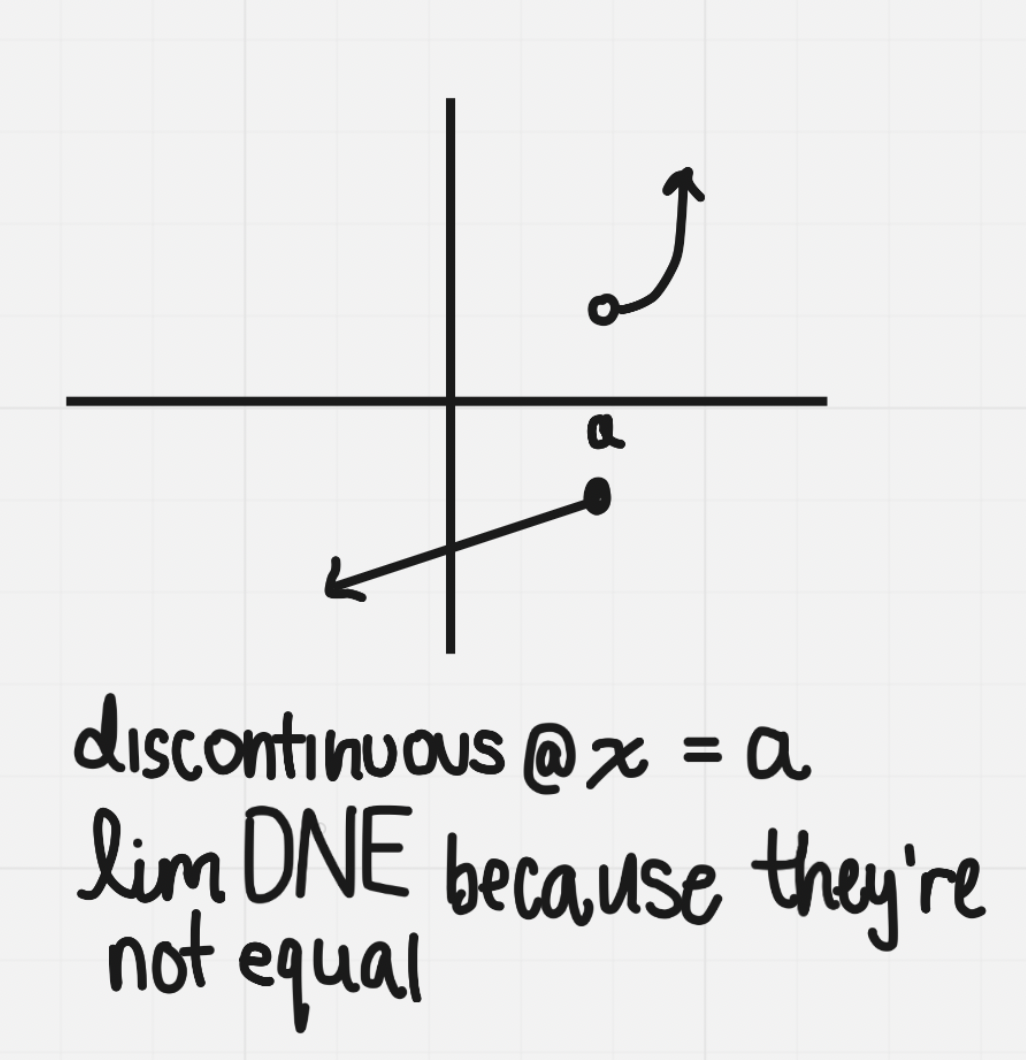
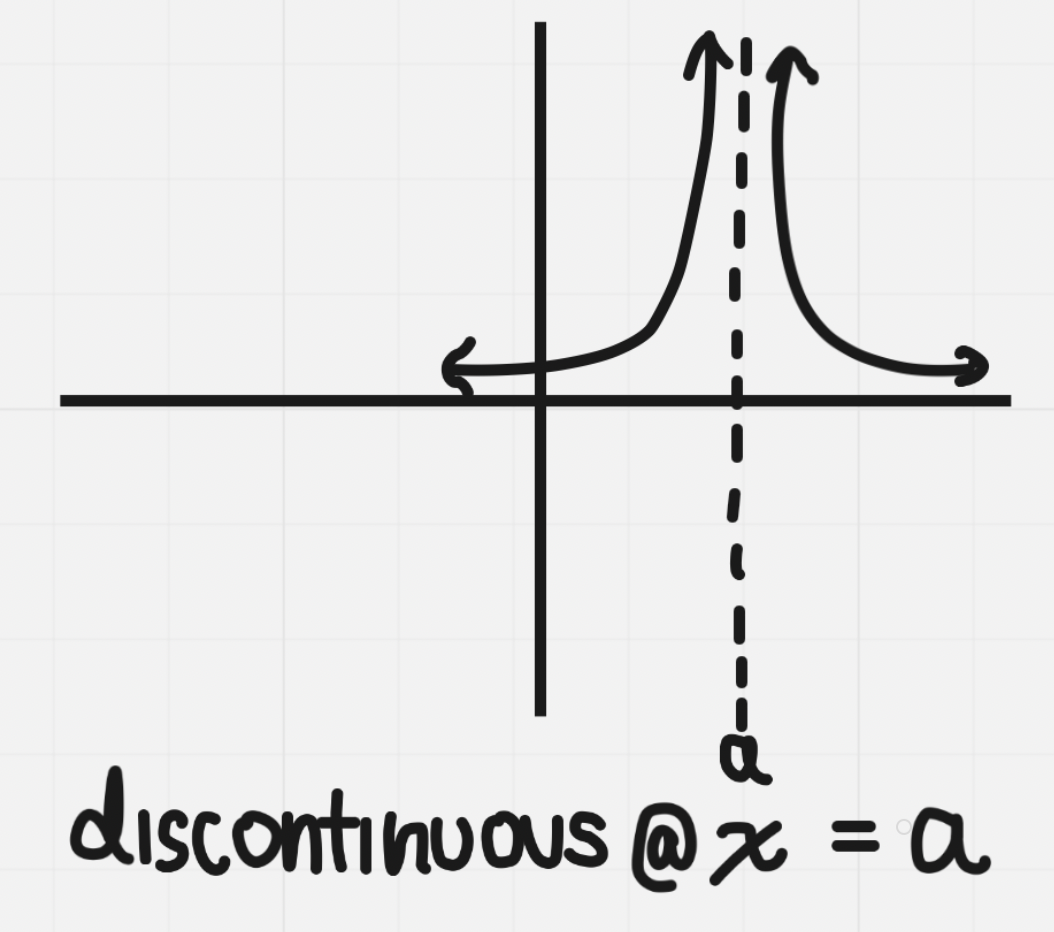
Infinitely discontinuity: one sided limit is infinite so limit doesn’t approach a particular finite value and limit does not exist

Properties of Limits: Evaluating Limits Algebraically

• Any constants are equal to their limit
• The limit of x as x approaches a is = to a
• The limit of a sum is the sum of the limits
• The limit of a difference is the difference of the limits
• The limit of a constant times a function is the constant times the limit of the function
• The limit of a product is the product of the limits
• The limit of a quotient is the quotient of the limits, provided that the denominator ≠ 0
• The limit of a power is the power of the limit, provided that the exponent is a rational number
• The limit of a root is the root of the limit provided that the root exists

Direct substitution: When you are evaluating a limit, you can substitute your a value in for x within the function to find it

• This doesn’t always work though because it may result in 0/0 (intermediate form)

Intermediate form: 0/0 as a result, we cannot conclude that this limit DNE so we need more tools to determine the limit. The tools we use are factoring, rationalizing both numerator and denominator, and simplifying and expanding

Derivatives

Differentiation: output is called the derivative which can be used to find the slope of the tangent at any point in the function’s domain

First Principles Defintion of the Derivative

• The difference quotient with a swapped out for x

• h is 0 because this is the smallest interval between 2 numbers

  

When this limit is simplified by letting h → 0, the resulting expression is expressed in terms of x

• This expression can be used to determine the derivative of the function at any x-value in the function’s domain
• In the end, you shouldn’t have any h’s left as they should all be swapped for 0 after simplifying

f’(x) is a way to communicate that it’s a derivative