Calculus BC | Unit 10A

FS 2024

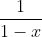
Power series for 1/1-x

1+ x + x² + x³ + … + x^n + …

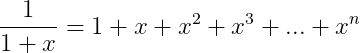
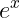
Power series for eˣ

1 + x/1! + x²/2! + x³/3! + … + x^n/n! + …

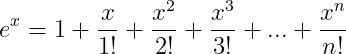
You can transform a series by. . .

1. anti-differentiating (take the antiderivative, remember c)

2. differentiating

3. multiply/divide

4. add/subtract (shift vs. modifying every x)

You can only substitute when transforming a series if. . .

the center remains correct.

You must use Taylor’s theorem if algebraic adjustments cannot be made.

The sum of a geometric series can be found with. . .

a/1-r

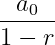
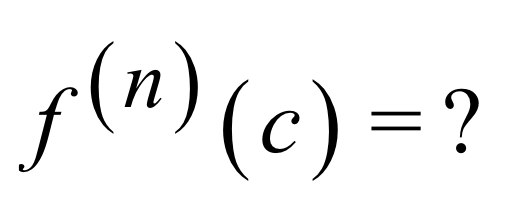
The nth derivative of a T series can be found with. . .

Coefficient of x^n term * n!

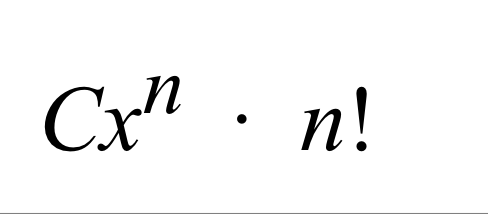
If f’’(x) is positive then. . .

f is concave up at that x value.

If f’’(x) is negative then. . .

f is concave down at that x value.

2nd derivative test for local extrema

1. use the 1st derivative test and endpoints for critical values (f’(x) = 0)

2. if f’’(x) = +: concave up, local minimum.
   if f’’(x) = -: concave down, local maximum.

2nd derivative test for absolute extrema

1. find critical points where the first derivative f’(x) = 0 or undefined (endpoints)

2. calculate 2nd derivative for all (positive = local min, negative = local max)

3. find original f(x) values for all of the locals & select the highest and lowest values.

When to use tangent line approximation vs. the sum equation for an infinite series

Sum of an Infinite (Geometric/Known) Series

• Exact

• “compute the sum”

• “determine the convergence of the series”

Tangent Line Approximation

• approximating values near a specific point
  “approximate the value of function g(t)”

A geometric series will converge if

|r| < 1

Conditions for finding the exact value/sum

1. Series must converge (geometric: |r|<1)

2. X must match the given range*

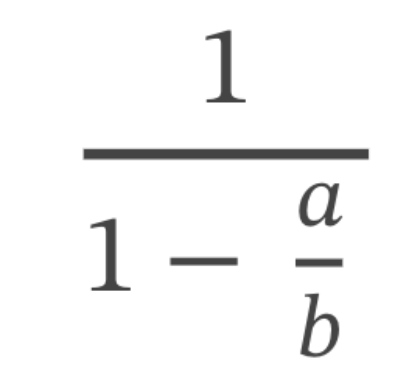
Fraction rules:

1/(1-a/b) = ?

b/(-a + b)

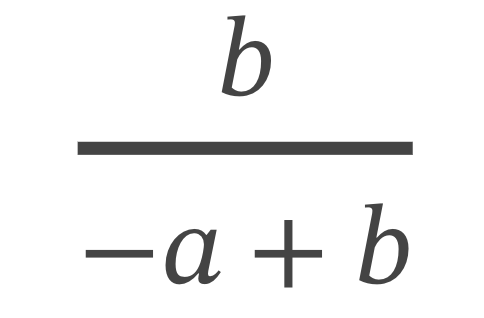
Tangent line approximation formula

f(x) ≈ f’(a)(x-a) + f(a)

0!

=1

f(x) * g(x)

PRODUCT RULE

f’(x)g(x) + g’(x)f(x)

f(x)/g(x)

QUOTIENT RULE

f’(x)g(x) - g’(x)f(x) / f(x)²