Boolean Operators etc

Boolean Operators

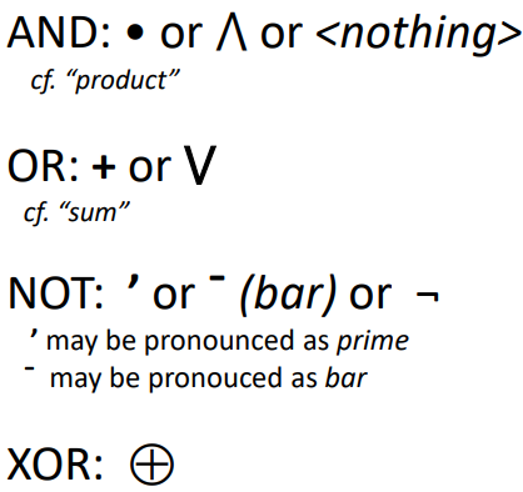
Truth Tables and Gates

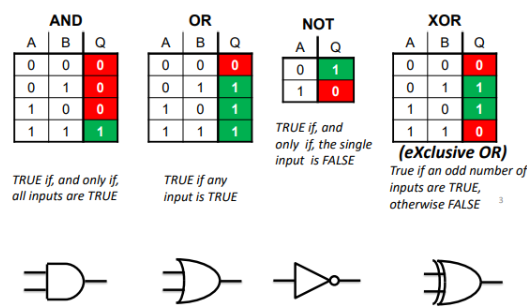
Inverted Logic Operators

In practice, different gates, called NANDs and NORs, are very commonly used instead of AND/OR/NOT/XOR gates

• A NAND B = (A AND B)’ 

• A NOR B = (A OR B)’

This is because NAND and NOR are “universal”: any binary logic circuit can be built entirely from NAND gates, or from NOR gates

• Also: using only NANDs (or NORs) makes circuit design significantly more cost-effective, as only one type of component is needed 

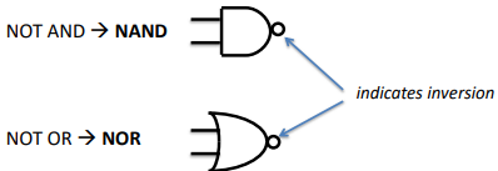
Building AND/OR/NOT from NAND/NOR

Boolean Algebra

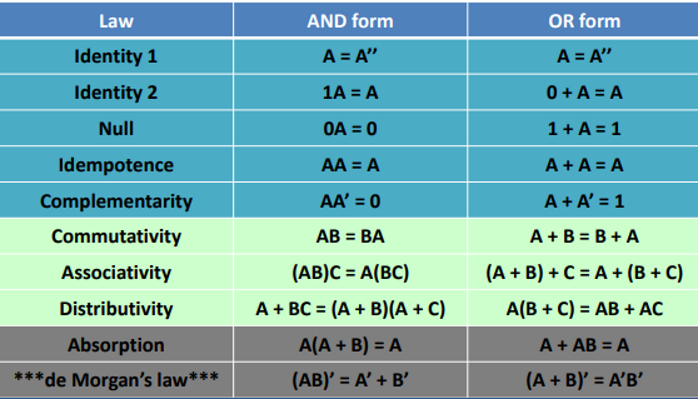
De Morgan’s Law

•  (AB)’ = A’ + B’         (A + B)’ = A’B’ 

Whenever we see an expression whose subexpressions are all ANDed together, or all ORed together, we can re-state by

1. negating the overall expression

2. negating the sub-expressions

3. flipping the operators from OR to AND, or vice versa

Designing Logic Circuits

• Write out a truth table for the desired logical function

• Derive a boolean expression by ORing together all the rows whose “output column” is 1

  • This is often called the sum-of-products form (cf. arithmetic “+”)

• Translate the Boolean expression to logic gates

  • May need to map to AND/OR/NOT gates or to NAND or NOR only

  • May need to use Boolean algebra or “Karnaugh maps” (se

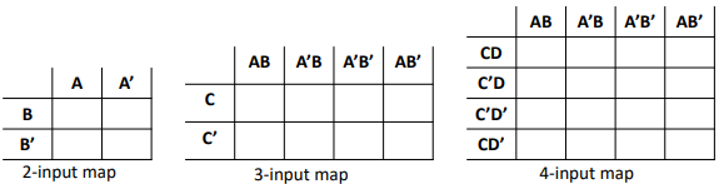
Karnaugh Maps

• A grid in which each square represents one possible combination of inputs

• Columns/rows are ordered so that only one input “changes” from col-to-col, and from row-to-row

• ‘Wrap’ left-to-right and top-to-bottom

• Pick a template with the required number of inputs, and put a 1 in any square for which we want an output of 1 

Solving a Karnaugh Map

Look for rectangular groups of 1s

• Groups must contain 2 or 4 or 8 … (2n ) cells

• Groups may overlap, and may wrap around the edges

• The larger the groups, and the fewer the groups, the better 

Result: for each group simply list the “unchanged” terms and OR them together (“changed” ones “cancel”)