congruences

Ça signifie quoi a ≡ b [n]

« a est congru à b modulo n »

Ou

« a et b sont congrus modulo n »

→ a et b on le même reste dans la |- par n

Comment on écrit « x n’est pas congru à y » ?

x ≢ y

Quel est le reste de 2 |- 5 ?

2

5×0+2

Montrer que le produit de 3 entiers consécutifs est un multiple de 3 ?

On prend tous les restes initiaux possibles

Puis on observe les restes possibles des deux termes qui suivent dans chaque cas

On trouve qu’après qu’on additionne les 3 dans tous les cas le reste est forcément égal à 0

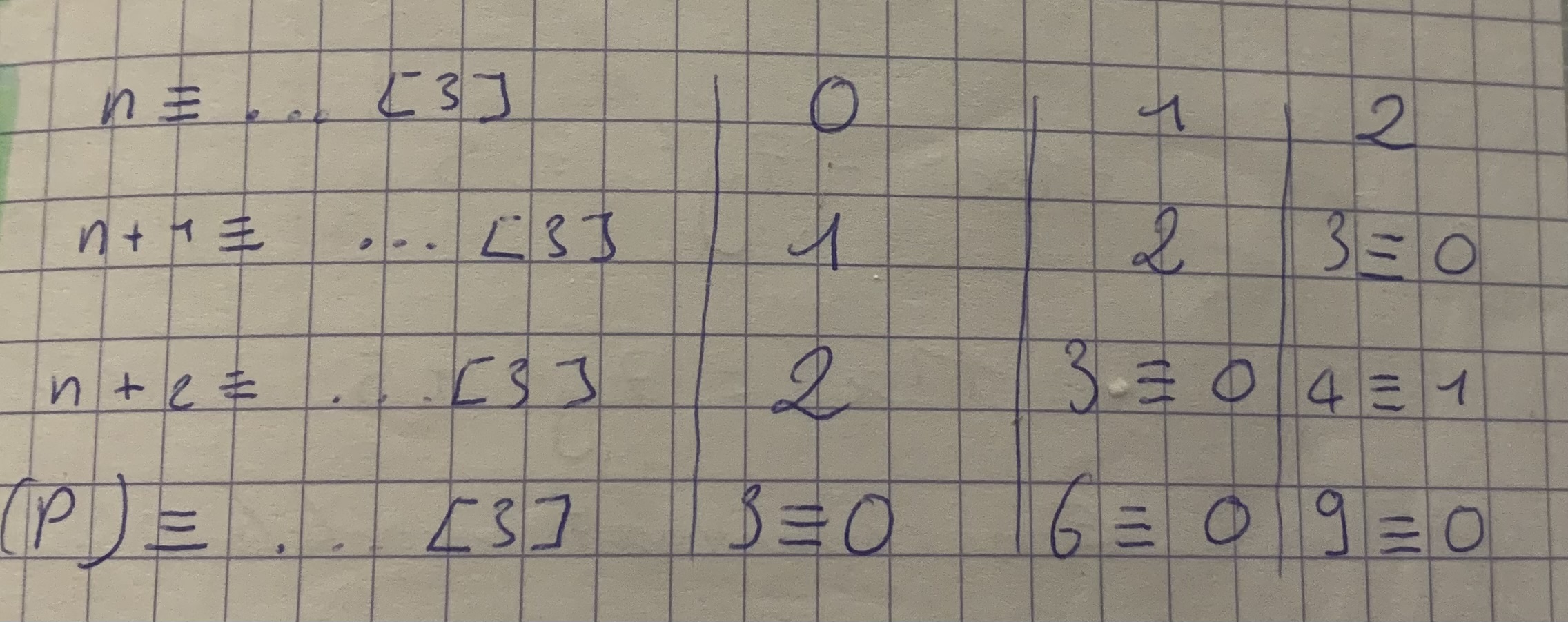
Comment j’écris 2x ≡ 4 [12] sous une autre forme ?

2x = 12q + 4

C’est quoi \frac{Z}{nZ} ?

L’ensemble des restes modulo n

Ex. Z/4Z = {0;1;2;3}

Comment simplifier notre manière de voir

7x²-4y² = 1 (dans Z) ?

Au lieu de l’étudier dans Z, on peut l’étudier dans Z/4Z car

-4y² ≡ 0 [4]

Donc on cherchera 7x² ≡ 1 [4]

Comment on trouve 7x² ≡ 1 [4] ?

À quoi ça sert de travailler une équation modulo quelque chose au lieu de la travailler dans z ?

• Vérifier si l’équation admet une solution

• Ensuite si l’équation admet des solutions modulo truc, il faut vérifier que ces solutions existe dans Z en ré-écrivant l’équation initiale grâce au solution trouvées sous la forme d’une |-

Résoudre 3x² + 7y² = 10^(2n)

Modulo 7

• Réduire au minimum chaque terme modulo 7 ( 7y²≡0 [7], 10^(2n) = 100^n ≡ 2^n [7] et 3x² ≡ 3x² [7] )

• Réécrire l’équation modulo 7 (ici 3x² ≡ 2^n [7] )

• Calculer d’une part tous les restes modulo 7 de 3x²

• Observer le cycle des puissances de 2^n (ici on observe que les n congrus à 0 [3] donnent un 2^n congru à 1[7], les n ≡ 1 [3] → 2^n ≡ 2 [7] et les n ≡ 2[3] → 2^n ≡ 4[7] )

• Plus qu’à comparer est-ce que parfois les restes sont les mêmes

Comment je trouve pour quel n une expression est congrue à u [m]

Ou

Pour quel n le reste d’une expression |- m vaut u

J’écris le tableau de congruence modulo m

n peut être congru à 0 1 2 3 etc.

Puis à chaque ligne j’applique une nouvelle opération à n et à tous ses restes

Jusqu’à obtenir l’expression, et alors je regarde pour quel n le reste est u

Calculer le reste de u^f |- v ?

• à combien est congru u [v] ? u’

• On regarde le cycle de puissance de u’^n → tout les combien de n est ce que le résultat, quand on prend son reste dans la division par v redevient la même (ce nombre de n on l’appelle w)

• À combien est congru f [w] ? f’

• On peut réécrire u^f |- 7 en u’^f’ ≡ (calculé à l’étape 2) [7]