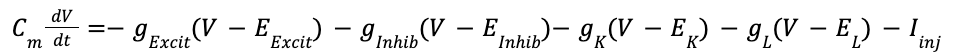NSCI 303 - Exam 1

What is a Turing machine?

A Turing machine is a theoretical computing device, proposed by Alan Turing

The machine has a finite number of internal states and has a sensory system to read, write, or erase. It reads symbols on a tape. Depending on the symbol, it can change the internal state, and the machine can change the symbol on the tape or leave it alone. Then it moves the tape to the left or right.

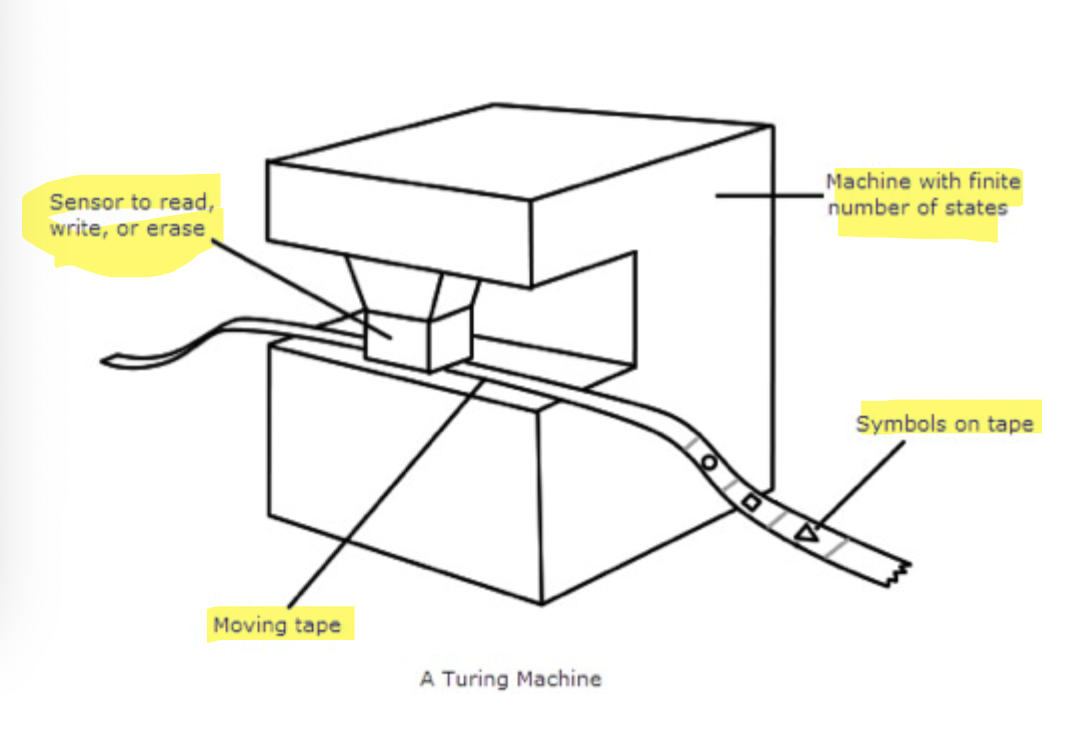
How does one represent a Turing machine?

A list of values following the structure

{internal state}{symbol on tape} → {new internal state}{mark tape}{move L or R}

What is a Universal Turing Machine?

A theoretical machine that can imitate any possible Turing machine

Describe some early steps in the development of machines that imitate what humans brains do

• Vaucanson’s mechanical duck (1764)

  • It can flap its wings, move its head, and simulate digestion

  • Early attempt to mimic biological processes mechanically

  • Not a true thinking machine

• Charles Babbage – Analytical Engine (1833)

  • Precursor to modern computers

  • Designed to perform general-purpose calculations using punched cards

  • Was not ever completed

• George Boole (1854)

  • Developed Boolean algebra, a mathematical system using binary logic (true/false or 1/0)

• EDSAC – first working modern computer (1949)

  • First practical stored-program computer

Properties of the lipid bilayer and their significance

Lipid bilayer has a hydrophobic core that allows selective permeability that permits

Hydrophilic heads, hydrophobic tails

Amphipathic phospholipid molecules (Hydrophilic heads, hydrophobic tails)

Channels and transporters are embedded to control movement ions and molecules

Neuropile is a mixture of axons and dendrites

Black blobs in the axon are mitochondria

Be able to write down the simplified Nernst equation and calculate equilibrium potentials

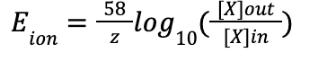
Know the major ionic concentration gradients across the membrane

What is a conditioned reflex? Who was Donald Hebb? What is Hebb’s rule?

Donald Hebb was a psychologist that proposed ‘Hebbian learning’, where ‘Cells that fire together, wire together’

If two neurons are repeatedly active at the same time, the connection between them strengthens

Ex. Initially, synapse a is strong, and synapse b is weak so ringing the bell has no effect on C. If A and B fire at the same time, B and C will be active at the same time. Thus, synapse b is strengthened via Hebb’s learning rule. Eventually, B on its own can cause salivation.

Be able to write down the equation relating current flow, conductance, voltage and the equilibrium potential

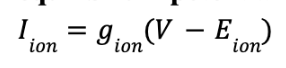
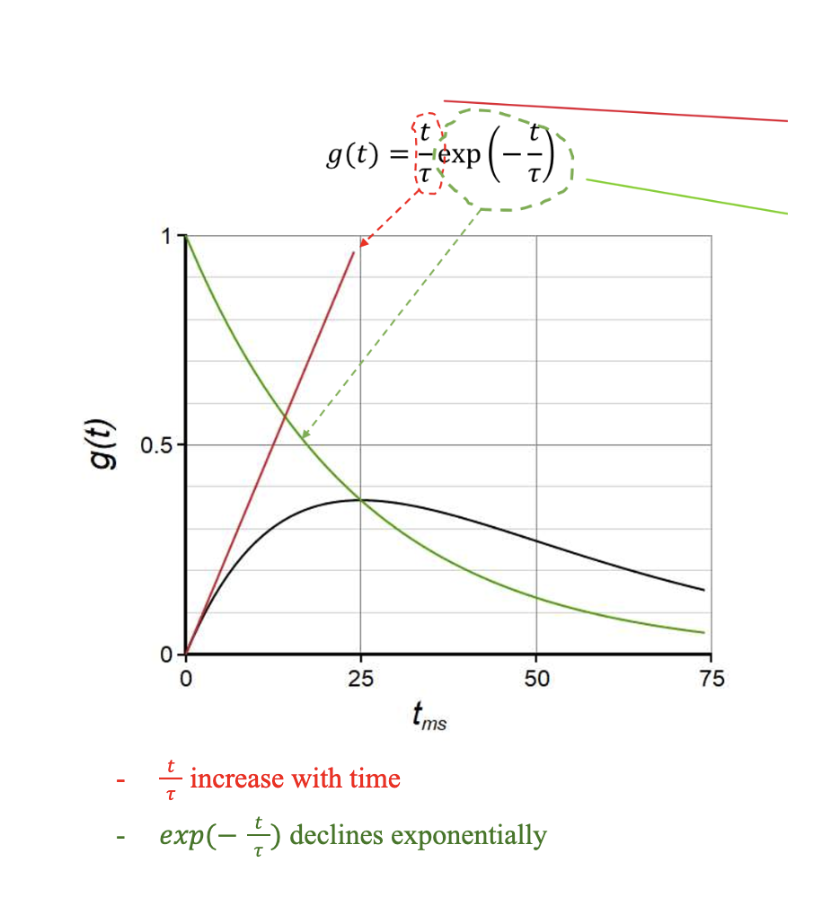
What is an alpha function and what is it used for?

• An alpha function models the time course of synaptic conductance changes following a neurotransmitter release

  • g is the conductance of the ion channel(s) affected by the transmitter

  • 𝜏 is the time course constant

  • t is the time following synapse activation

Draw the equivalent circuit diagram of an excitable neuron membrane?

Who were Hodgkin and Huxley and what are they famous for?

Andrew Huxley and Alan Hodgkin were neuroscientists known for solving the Hodgkin-Huxley equations, a mathematical model for describing how action potentials are initiated and propagated. Made this model based on careful, systematic empirical observation of experimental data.

What is ‘voltage clamp’?

The voltage clamp is circuitry which maintains the voltage of the system at a fixed level, which is done by delivering the right amount of current. You can then measure current flow, making it easier to interpret the system’s behaviours in terms of ion movement.

m3h and n4– what do they mean and what ion channels do they apply to?  

m3h represents the gating particles of voltage-gated sodium channels in the cell, and whether they are open or closed. The m represents the probability of 3 activating gates being open and the h gate represents the probability of 1 inactivation gate being open. When multiplied by peak Na conductance in the cell (g bar Na), this value shows Na conductance changes throughout the action potential. 

n4 represents 4 potassium gating particles and the probability of them being open. When multiplied by g bar potassium (peak K conductance), they show K conductance changes throughout the action potential. 

From the above you ought to be able to write down the main HH equation.

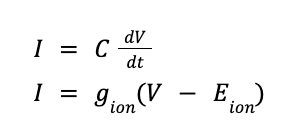
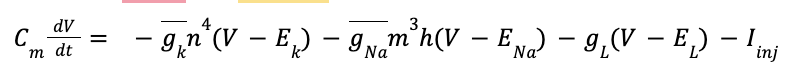
Where g_L (V - E_L) is equal to the leak channel current. (Writing the main HH equation probably won’t be on the exam but we should be comfortable with it) 

Describe the sequence of changes in current flows during the action potential.

During the AP, there is a fast positive self-terminating feedback loop. Depolarization opens Na+ channels which causes more depolarization. The inactivation gate causes self-termination. There is also a slow negative feedback loop where depolarization opens K+ channels and increases K+ conductance closer to Eion K+ and hyperpolarizes the cell.

Negative feedback loop stabilizes things.

What is meant by the term length constant and what factors determine it? (The equation will help.)

Describe what compartmental modelling is. What are its goals and what data are needed to do it?

Compartmental modelling takes an accurate geometrical model of a neuron and breaks it down into unbranched compartments, taking into account temporal dynamics and channel distribution between compartments. Creates a more accurate model of a neuron compared to simply a passive cylinder.

DATA NEEDED:

Accurate shape measurement of cell body, dendrites and spines

Passive membrane properties: Rm, Cm, Ri

Distributions of ion channels in cell body and neurites

Properties of channels (i.e. voltage-gated)

Synaptic input distribution

Conductance change and time course for each synapse

Define some of the questions compartmental modelling is intended to address. How might spine geometry be related to function?

Designed to address questions like:

What is the importance of spike timing in determining the firing of a post-synaptic neuron?

Can temporal patterns in the inputs be reproduced in the outputs or does information get lost?

Describe the question addressed by Mainen and Sejnowski and what they were able to show with modelling.

Mainen and Sejnowski showed that the shape of neurons may have a significant impact on the firing pattern of the neuron. 

• Unique patterns based on shape -> same current was injected to all neurons (Iinj was constant)
  

Conclusions from Mainen and Sejnowski:

• Shape has to do with function

• Compartmental modelling is quite good

What issues limit what can be done with the technique of compartmental modelling?

Still not fully understood, temporal patterns are important in inputs but can they be reproduced in outputs?

made assumptions

high processing power for all the compartments is needed

estimations of properties and distance

measurement limitations, hard to compare with experimental data

cannot capture all biophysical processes

Describe how the IF model works – what are the assumptions and simplifications?

The IF model is a simplified model used to describe the behaviour of neurons. The membrane potential integrates inputs over time and, once it reaches a certain threshold, it "fires" an action potential.

Assumptions:

Ignores cell shape: Assumes the neuron’s geometry doesn’t affect its behaviour

Different from compartmental modelling

Ignores Hodgkin-Huxley: Doesn’t take into account the ion channels or their conductance properties over time

Ignores spatial distribution of channels: Locations of ion channels across the membrane affects the behaviour of the neuron like shunting

Ignores distribution of synapses on the cell: Where the synapse is can affect the level of depolarization

What are the benefits of using the IF model? What is lost?

• Simple and efficient: 

  • Suitable for large networks 🐩

  • Manageable computational complexity

  • Don’t have to take HH equation into account for each neuron (simplified) 

• Lose: 

  • Complexity (not taking into account neuron shape, realism)

  • Technically HH is lost too but not as important 

What behaviours the term ‘integrate’ refer to?

The gradual accumulation of inputs (EPSPs or IPSPs) until it reaches the threshold for an action potential.

Take the HH equation and remove what is necessary to get the basic IF equation.

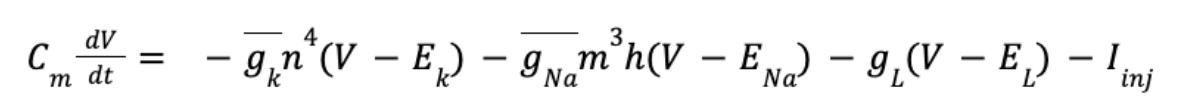
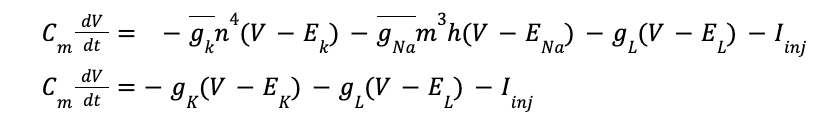
Include terms for inhibitory and excitatory conductances.