Lecture 20: factorial design (part 2)

what’s the difference between a control variable and a control condition?

• variable: variable that is held constant across all levels of the IV (something that could influence your results but that you don’t want to measure, ex: light, time)

• condition: one level of the IV that doesn’t receive the treatment (ex: not receiving a vaccine)

why would you have control variables?

to make sure that the IV explains the changes in the DV (internal validity)

*control variable: variable that is held constant across all levels of the IV (ex: lighting, time of day)

why would you have a control condition?

to compare the participants who received the treatment and participants who didn’t

*control condition: one level of the IV that doesn’t receive the treatment

true or false: a control condition can be a control variable (and vice-versa)

false: a control condition applies to one level of the IV (varies with the IV) while a control variable is kept constant

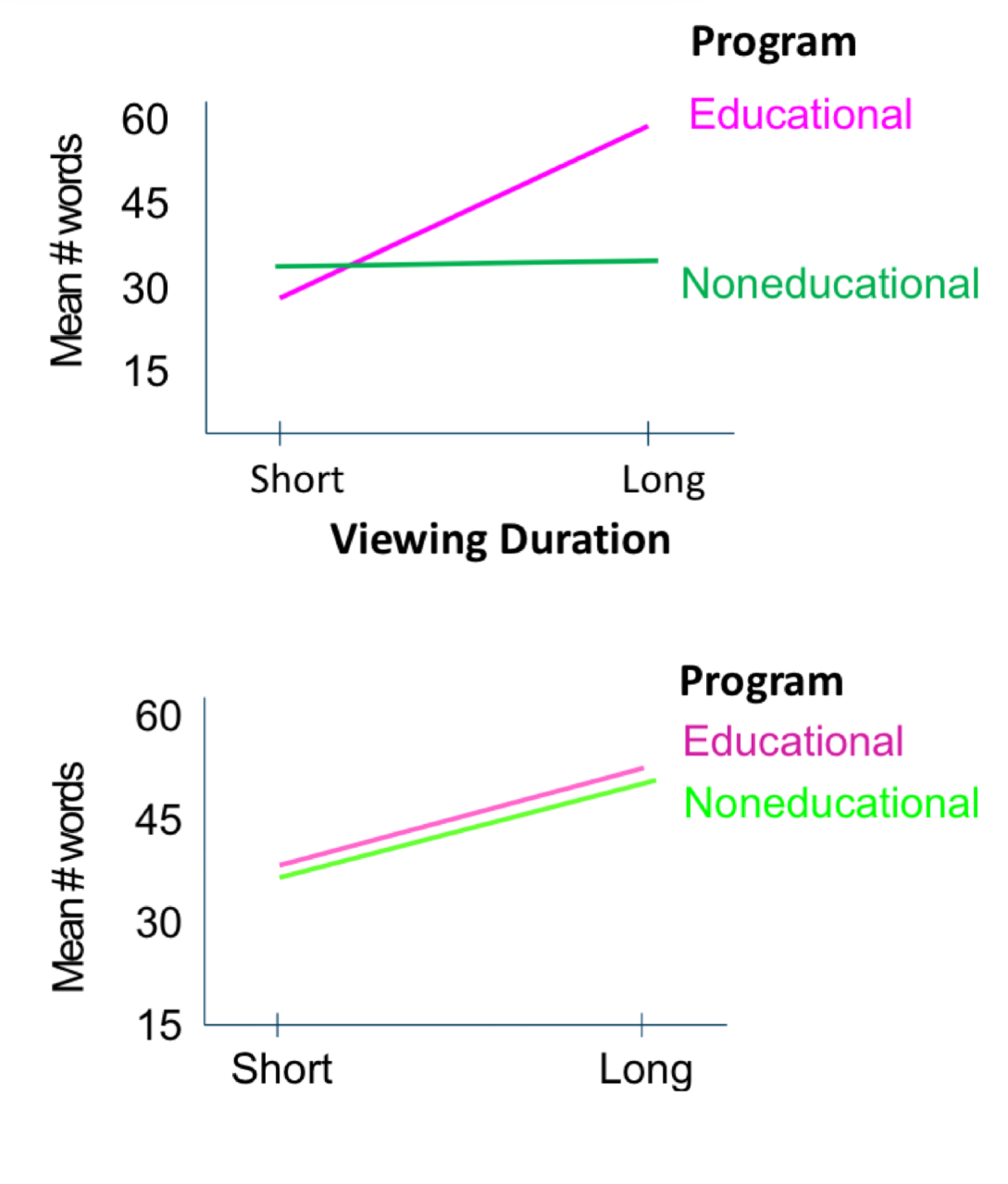
explain the difference between these two graphs knowing that

• factor A: TV viewing duration

• factor B: TV program

• DV: toddler’s vocabulary

• top graph: viewing duration (factor A, x-axis) impacts the number of world learned (DV, y-axis) depending on the program (factor B, lines)

  • interaction because the lines aren’t parallel

• bottom graph: TV viewing duration (factor A, x-axis) will increase the number of words learned (DV) regardless the TV program (factor B, y-axis)

  • no interaction: lines are parallel

what are the types of factorial designs? (3)

• pure (between-subjects) factors

• within-subjects factors

• mixed designs (between + within-subjects factors)

define “higher order factorial designs”

factorial designs with 3 or more factors

define “pure factorial designs”

• AKA between-subjects factorial design

• all factors are being manipulated across participants

• different groups of participants are randomly assigned to each condition (one participant goes in one condition)

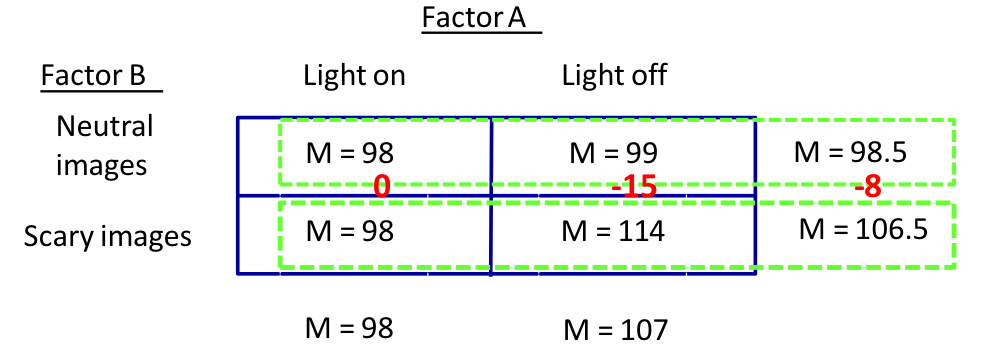
in this pure factorial design, is there a main effect of A, a main effect of B and an A x B interaction?

• main effect of A: 98 ≠ 107

• main effect of B: 98.5 ≠ 106.5

• interaction: 0 ≠ -15 ≠ -8

what’a the advantage (1) and the disadvantages (2) of pure factorial designs?

advantage:

• no order effect problem (because each participant only experiences the condition once)

disadvantages:

• between-subjects, so could require a lot of participants

• individual differences can become a confounding variable

when should you choose a pure factorial design? (3)

• a lot of participants are available

• individual differences are small

• order effects won’t be a problem

define “within-subjects factorial designs”

one group of participants goes through all condition

when you change the size of a factorial design (ex: go from 2×2 to 3×3), the number of participants will be affected in a [between/within] subjects factorial design

between only: participant in one condition only

what are the advantages (2) and disadvantages (2) of within-subjects factorial designs?

advantages:

• fewer participants needed

• reduces individual differences

disadvantages

• more factors = participants go through more condition

• time consuming, higher chances of attrition (lose participants)

when should you use a within-subjects factorial designs? (2)

• a lot of individual differences

• order effects aren’t a problem

define “mixed design”

factorial design that combines one between-group and one within-group design

when should you used mixed factorial designs?

when you want the advantages of a between-subjects design for one factor, but also the advantages of a within-subjects design for the other factor

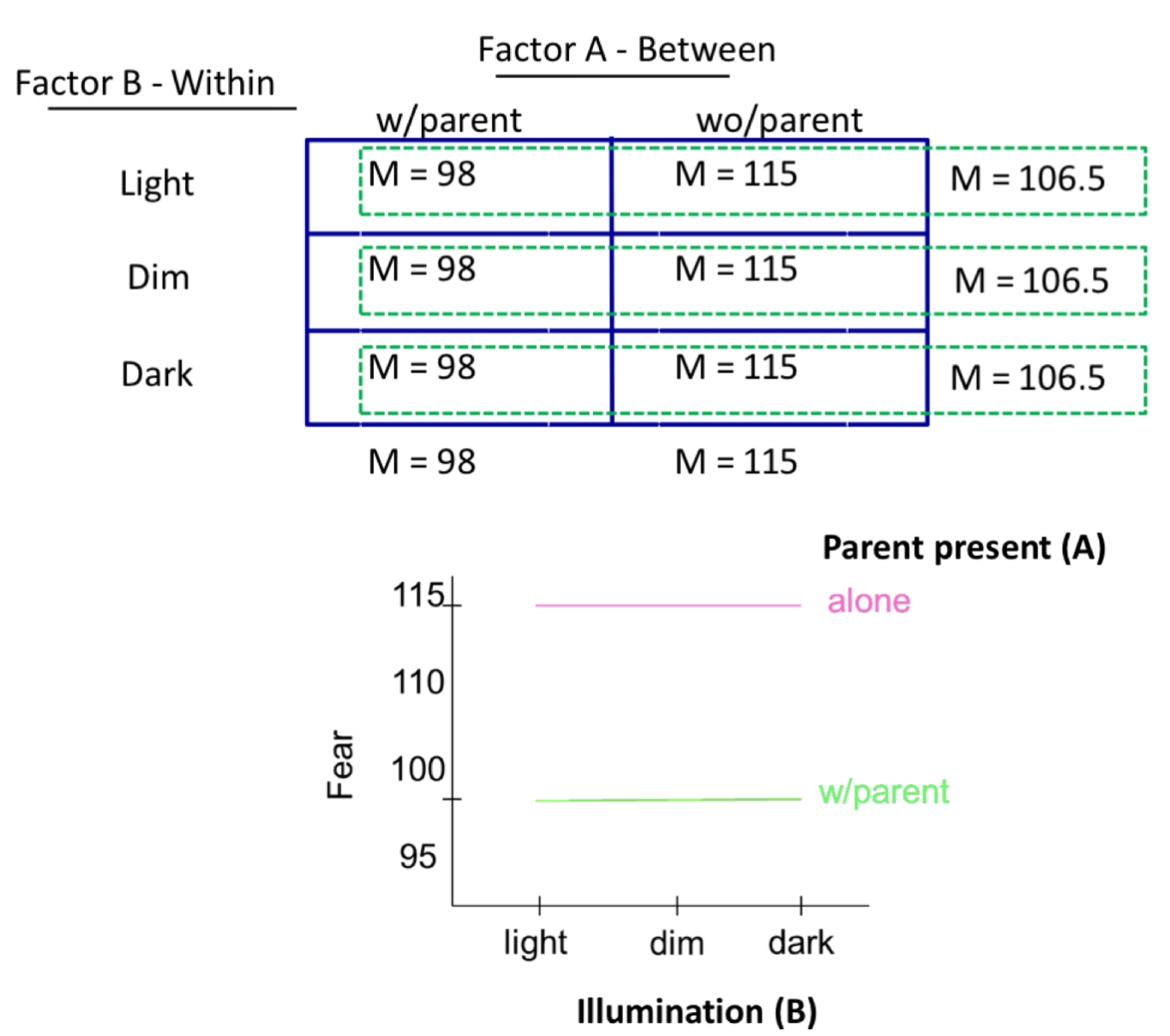
in this mixed factorial design, is there a main effect of A, a main effect of B an an interaction?

• main effect of A: 98 ≠ 115

• no main effect of B: 106.5 = 106.5 = 106.5

• no interaction: lines are parallel

when you have pretest and posttest groups, you’re doing a [between-within]-subjects factor

within: pretest before treatment and posttest after treatment

in a three-factor design, how many main effects and interactions are you measuring?

• main effect: 3 (A, B, C)

• interactions: 4 (A×B, B×C, A×C, A×B×C)

in this four-factor design where we measure the correctly recalled items, you have these factors. which are between-group and which are within-group:

• gender: male/female/non-binary

• age: older adult/middle adult/young adult

• time of day: morning/afternoon/evening

• types of word: concrete/abstract

• gender: between-group (you can’t be in multiple gender groups)

• age: between-group (you can’t be in multiple age groups)

• time of day: within-group (counterbalance so that we measure participants at multiple day times)

• types of words: within-group (we can present both types of words to the participant)

true or false: higher order interactions can become complex

true: especially if you have more than 3 factors, you will have a hard time predicting interactions

consider a 3 (gender) x 3 (age) x 2 (word type) x 2 (morning/evening) design. determine the number of factors (x-way) present in the findings: “females in the middle adult and young adult groups remembered abstract words better than concrete words in the evening”

4-way:

• “females”: difference, no male or non-binary

• “middle and young adult”: difference, no old adult

• “abstract better than concrete”: difference, abstract VS complex

• “evening”: difference, no afternoon or evening

consider a 3 (gender) x 3 (age) x 2 (word type) x 2 (morning/evening) design. determine the number of factors (x-way) present in the findings: “males in the older and middle adult groups remembered both abstract & concrete words well in the morning“

3-way

• “males”: difference, no females or non-binary

• “older and middle adults”: difference, no younger adults

• “both abstract and concrete”: NO difference

• “morning”: difference, no afternoon or evening

what are the advantages of a factorial design? (3)

• efficient and allows you to study multiple things

• instead of reducing individual differences by holding factors constant, it can add that difference as a factor

• higher external validity: measure multiple variables and people differ from multiple variables

what does a factorial design allows us to study? (3)

• effects of many factors at the same time

• interactions of factors

• replication and expansion of an existing study: you can replicate and add another variable

what are the disadvantages of a factorial design? (4)

• more chances of having confounds and control for them

• if the factors aren’t manipulated, interpretations aren’t better than correlational studies

• too many factors are confusing to interpret

• might require higher alpha levels due to multiple statistical tests

what do we do in a statistical analysis of a factorial design? (2)

• compute the means for each treatment condition (cell)

• use ANOVA to evaluate the statistical significance of the mean differences

what are some other uses of factorial designs? (3)

• replication: repeating a previous study and add new factor

• expanding: add a factor in the form of a participant characteristic to reduce variance (for between-subjects only according to book)

• use order of treatments as an additional factor to reduce variance (for within-subjects only)

what’s the difference between replication and expansion?

• replication: do again and add a new factor

• expansion: do again, but add a participant characteristic factor to reduce variance

when you add order of treatments as an additional factor, what are the possible outcomes? (3)

• no order effect: no order effect existing

• symmetrical order effects: same order effects across other factors (A-B = B-A → A influence B like B influence A)

• asymmetrical order effects: order interacts with other factors (A-B ≠ B-A)

how does adding the order of treatments as an additional factor reduce variance? (2)

• randomization of participants to conditions doesn’t not reduce bias from extraneous variables (different order does reduce bias)

• it’s not always possible to randomize all conditions orders when there are many conditions