CS 182

Discrete math

Study of math structures that correspond to natural numbers

Graph

Finite set of nodes paired by edges

Undirected graph

Uses unordered pairs

Directed graph

Uses ordered pairs

Conjunction

AND

^

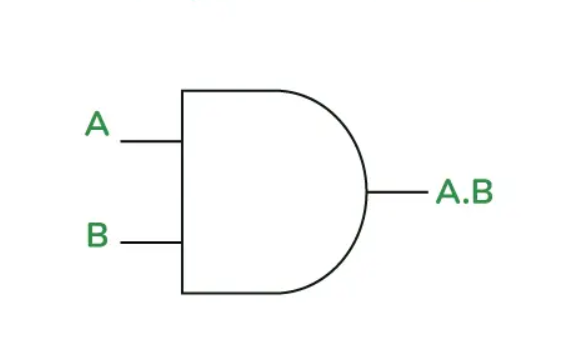
Inverse Conjunction

NAND

-^

Negation

NOT

-A

Disjunction

OR

v

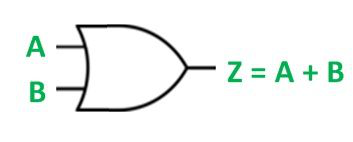
Inverse Disjunction

NOR

-v

XNOR

⊙

XOR

⊕

Implication

IMPLIES

⇒

• True, except when true implies false

• Not commutative

Anti-implication

NIMPLY

⇏

Proposition

A statement that is either always true or always false

Standard proposition variables

p

q

r

Logical connective

An operation that gives a binary output based on two propositions

Biconditional

⇔

• True if both propositions are of the same validity

• Equal to p→q ^ q→p

Converse

p→q

q→p

Inverse

p→q

-p→-q

Contrapositive

p→q

-q→-p

• Converse inverse

Relation between implication and contrapositive

Implication and contrapositive are equivalent

Truth table

Table containing all permutations of propositions and their connective outputs

Proof by contradiction

If the negation of a truth leads to a contradiction, the original proposition must have been true

Tautology

Statement that is always true

Contradiction

Statement that is always false

Equivalent Propositions

Logically Equivalent

Propositions have the same truth value in all cases

Biconditional is true

Implication To Or Identity

p→q = -p v q

Logical Identity Laws

p ^ T = p

p v F = p

Logical Domination Laws

p v T = T

p ^ F = F

Logical Idempotent Laws

p v p = p

p ^ p = p

Logical Negation Laws

p v -p = T

p ^ -p = F

Logical Commutative Laws

p v q = q v p

p ^ q = q ^ p

Logical Associative Laws

p ^ q ^ r

p v q v r

These can be evaluated in any order

Logical Distributive Laws

p v (q ^ r) = (p v q) ^ (p v r)

p ^ (q v r) = (p ^ q) v (p ^ r)

Logical Absorption Laws

p v (p ^ q) = p

p ^ (p v q) = p

Logical DeMorgan’s Laws

-(p ^ q) = -p v -q

-(p v q) = -p ^ -q

Satisfiable

Proposition is true for some case

Propositional Functions

Generalization of propositions

• Include all cases for a proposition

∀

Universal quantifier

• True for all x in U

∃

Existential quantifier

• True for some x in U

∈

Restricted to

Element of

Priority between connectives and predicate logic

Predicate logic takes precedent over connectives

Predicate Logic Equalities

-∃xJ(x) = ∀x(-J(x))

• If the proposition is not satisfied for some x, the proposition is false for all x

-AxJ(x) = ∃x(-J(x))

• If the proposition is not satisfied for all x, the proposition is false for some x

Communitive properties of AND and OR

AND and OR commute with themselves but not with each other

Distributive properties of ∀ and ∃

Cannot be distributed over logical connectives

Set

Unordered collection of unique elements

Element

Object in a set

N (Z >= 0)

Natural Numbers

Z

Integers

Z+ (Z > 0)

Positive Integers

R

Reals

R+ (R > 0)

Positive Reals

Q

Rational Numbers

C

Complex Numbers

Set equality

Sets have the same elements

• Repetition doesn’t matter

U (Set)

Universal set

Set of all elements within the context

∅

Empty set

Set with no elements

∅ ≠ {∅}

Empty set is not equal to a set with an empty set in it

• An empty set counts as an element

Interval notation

[a, b] = {x | a <= x <= b}

• Parentheses: Exclusive

• Brackets: Inclusive

⊆

Subset

A set containing some elements of another set

Subset equality

⊆ = ∀x(x ∈ A → x ∈ B)

Tautologies of subsets

S ∈ S

∅ ∈ S

⊂

Proper subset

A subset of a set which is not equal to the original set

Proper subset equality

⊂ = ∀x(x ∈ A → x ∈ B) ^ ∃x(x ∈ B ^ x ∉ A)

| |

Cardinality

Number of elements in a set

Finite set

Cardinality is a non-negative integer

Cardinality equality

Two cardinalities are equal if every element in each set can be mapped together algorithmically

Power set

The set of all subsets of a set

Power set cardinality

2ⁿ, where n is the original cardinality

Cartesian product

A x B = {(a, b) | a ∈ A ^ b ∈ B}

• Uses an ordered pair

• Set of all ordered combinations of elements from A and B

A ∪ B

{x | x ∈ A ^ x ∈ B}

Union

Set containing all elements of both sets

A ∩ B

{x | x ∈ A v x ∈ B}

Intersection

Set containing elements in common

A - B

{x | x ∈ A v x ∉ B}

Difference

Set of elements in A that are not in B

A ∩ -B

Principal of inclusion-exclusion

|A ∪ B| = |A| + |B| - |A ∩ B|

Set Identity Laws

A ∩ U = A

A ∪ ∅ = A

Set Domination Laws

A ∪ U = U

A ∩ ∅ = ∅

Set Idempotent Laws

A ∪ A = A

A ∩ A = A

Set Complementation Law

—A = A

Set Commutative Laws

Unions and intersections commute with themselves but not each other

Set Associative Laws

A ∪ B ∪ C

A ∩ B ∩ C

Both can be evaluated in any order

Set Distributive Laws

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Set DeMorgan’s Laws

-(A ∩ B) = -A ∪ -B

-(A ∪ B) = -A ∩ -B

Set Absorption Laws

A ∪ (A ∩ B) = A

A ∩ (A ∪ B) = A

Set Complement Laws

A ∪ -A = U

A ∩ -A = ∅

Function

A→B

Assigns each element of a set to one element of another set

Domain

The set of elements in the input set

Codomain

The set of elements in the output set

Range

The set of all elements that are images

Image

f(a) = b

The result of an element after a function

Preimage

f(a) = b

The input element

Function equivalence

Domains, codomains, and mapping are the same

Stirling’s Formula

n! ≈ √(2πn)(n/e)ⁿ

Injection

Function that is one-to-one

• If f(a) = b, f(b) = a

• If f(a) = f(b), a = b

Surjection

A function where all codomain elements have a preimage

Bijection

An function that is both an injection and surjection

⌊x⌋

floor(x)

Rounds down to the greatest integer less than or equal to x

⌈x⌉

ceil(x)

Rounds up to the least integer greater than or equal to x

Inverse function

f^-1(y) = x where f(x) = y

• Only exists on bijections

“Squeeze Theorem“ Proof Strategy

If a <= b, and b <= a, a = b

Relation

Association between elements of two sets

• More general than functions