Chapter 13: F Distribution and One-way Anova

Introductory

• Analysis of Variance: For hypothesis tests comparing averages between more than two groups

13.1 One-Way ANOVA

• ANOVA Test: determine the existence of a statistically significant difference among several group means.
• Variances: helps determine if the means are equal or not
• ANOVA Conditions
  • Each population from which a sample is taken is assumed to be normal.
  • All samples are randomly selected and independent.
  • The populations are assumed to have equal standard deviations (or variances).
  • The factor is a categorical variable.
  • The response is a numerical variable.
• Ho: μ1 = μ2 = μ3 = … = μk
• Ha: At least two of the group means μ1, μ2, μ3, …, μk are not equal. That is, μi ≠ μj for some i ≠ j.
• The null hypothesis: is simply that all the group population means are the same.
• The alternative hypothesis: is that at least one pair of means is different.
• Ho is true: All means are the same; the differences are due to random variation.
• Ho is NOT true: All means are not the same; the differences are too large to be due to random variation.

13.2 The F Distribution and the F-Ratio

• F-distribution: theoretical distribution that compares two populations

• There are two sets of degrees of freedom; one for the numerator and one for the denominator.

• To calculate the F ratio, two estimates of the variance are made.

  1. Variance between samples: An estimate of σ2 that is the variance of the sample means multiplied by n (when the sample sizes are the same.).

  2. Variance within samples: An estimate of σ2 that is the average of the sample variances (also known as a pooled variance).

     1. SSbetween: the sum of squares that represents the variation among the different samples
     2. SSwithin: the sum of squares that represents the variation within samples that is due to chance.

• MS means: "mean square."

• MSbetween: is the variance between groups

• MSwithin: is the variance within groups.

Calculation of Sum of Squares and Mean Square

• k: the number of different groups
• nj: the size of the jth group
• sj: the sum of the values in the jth group
• n: total number of all the values combined (total sample size: ∑nj)
• x: one value→ ∑x = ∑sj
• Sum of squares of all values from every group combined: ∑x2
• Between-group variability: SStotal = ∑x2 – (∑𝑥2) / n
• Total sum of squares: ∑*x^*2 – (∑𝑥)^2n / n
• Explained variation: sum of squares representing variation among the different samples→ SSbetween = ∑[(𝑠𝑗)^2 / 𝑛𝑗]−(∑𝑠𝑗)^2 / 𝑛
• Unexplained variation: sum of squares representing variation within samples due to chance→ 𝑆𝑆within = 𝑆𝑆total – 𝑆𝑆between
• df**'s for different groups (df's for the numerator)**: df = k – 1
• dfwithin = n – k*:* Equation for errors within samples (df's for the denominator)
• MSbetween = 𝑆𝑆between / 𝑑𝑓between: Mean square (variance estimate) explained by the different groups
• MSwithin = 𝑆𝑆within / 𝑑𝑓within: Mean square (variance estimate) that is due to chance (unexplained)
• Null hypothesis is true: MSbetween and MSwithin should both estimate the same value.
• The alternate hypothesis: at least two of the sample groups come from populations with different normal distributions.
• The null hypothesis: all groups are samples from populations having the same normal distribution

F-Ratio or F Statistic

• 𝐹 = 𝑀𝑆between / 𝑀𝑆within
• F**-Ratio Formula when the groups are the same size:** 𝐹 = 𝑛⋅𝑠𝑥^2 / 𝑠^2 pooled
  • where …
  • n: the sample size
  • dfnumerator: k – 1
  • dfdenominator: n – k
  • s2 pooled: the mean of the sample variances (pooled variance)
  • sx¯^2: the variance of the sample means

13.2 Facts About the F Distribution

• Here are some facts about the F distribution.
  • The curve is not symmetrical but skewed to the right.
  • There is a different curve for each set of dfs.
  • The F statistic is greater than or equal to zero.
  • As the degrees of freedom for the numerator and for the denominator get larger, the curve approximates the normal.

13.4 Test of Two Variances

• In order to perform a F test of two variances, it is important that the following are true:

  • The populations from which the two samples are drawn are normally distributed.
  • The two populations are independent of each other.

  

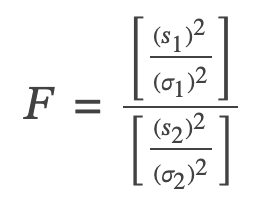
• F has the distribution F ~ F(n1 – 1, n2 – 1)

• where n1 – 1 are the degrees of freedom for the numerator and n2 – 1 are the degrees of freedom for the denominator.

• F is close to one: the evidence favors the null hypothesis (the two population variances are equal)

• F is much larger than one: then the evidence is against the null hypothesis

• A test of two variances may be left, right, or two-tailed.

  Examples

  \

\